Савчук підручник

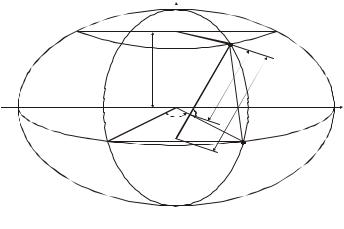
Розділ 2. Геометрія земного еліпсоїда

z bsinu const.

Ці формули показують, що площина z=const (рис 2.2) паралельна площині ху і перетинає поверхню еліпсоїда по колу радіуса r.

z

z

x z

Рис. 2.2

Коло u=const називається паралеллю, а параметр u – широтою.

Паралель з найбільшим радіусом r=a (z=0) називається екватором. Екватор ділить еліпсоїд на дві симетричні половини.

Криві =const є еліпсами і утворюються в результаті перетину поверхні еліпсоїда площинами, що вміщують вісь z. Вони називаються меридіанами, а параметр , який для поверхні еліпсоїда позначається буквою L– геодезичною довготою.

Якщо в рівнянні (2.9) виключити координати за (2.12), то отримаємо рівняння меридіана

53

Розділ 2. Геометрія земного еліпсоїда

Широта u та довгота L є криволінійними координатами точки на поверхні еліпсоїда; рівняння (2.13) – це рівняння еліпса, параметризоване широтою u, яка носить назву - п р и в е д е н а широта.

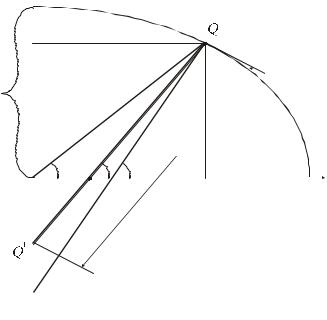
Приведена широта u може бути побудована геометрично. Візьмемо відрізок прямої, рівний великій півосі еліпсоїда, і відкладемо його так, щоб один кінець відрізка лежав на поверхні еліпсоїда в деякій точці Q , а другий – на осі обертання еліпсоїда в точці Q’ (рис 2.3)

Гострий кут, утворений відрізком QQ’ з площиною екватора, називається приведеною широтою.

Поверхня може бути задана також змінним радіусом– вектором r, та геоцентричною широтою Ф.

Геоцентричною широтою називається кут, утворений радіусом–вектором даної точки з площиною екватора.

n

Рис. 2.3

54

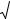
Розділ 2. Геометрія земного еліпсоїда

Із прямокутного трикутника OQB (рис2.3) отримаємо

Для того щоб встановити зв'язок геодезичної широти В з приведеною и, розглянемо який-небудь меридіан, наприклад, такий, площиною якого є площина zx (див. рис.2.2). Для цього меридіана L=const і його рівняння в параметричній формі отримаємо із рівнянь (2.10)

55

Розділ 2. Геометрія земного еліпсоїда

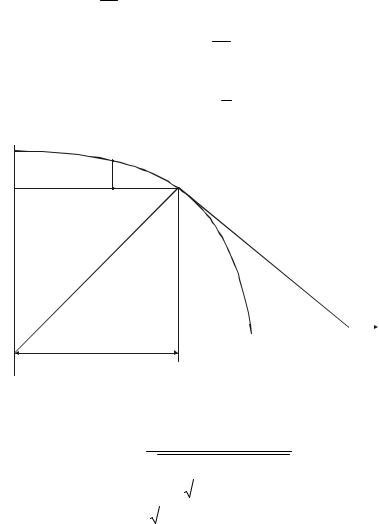
Тангенс кута, утвореного нормаллю з віссю х (рис.2.4),

dx

рівний похідній dz , взятій з оберненим знаком, тобто

dx tgB dz ,

або

a tgB tgu b .

Z

dr 900-B 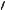-dr

z

90+B B

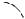
x/y

x

Рис. 2.4

Із останньої формули легко можна отримати

asinu

sin B 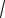a2 sin2 u b2 cos2 u ,

56

Розділ 2. Геометрія земного еліпсоїда

отримаємо наступні формули зв'язку між геодезичною B та приведеною u широтами

На основі формул (2.15) та (2.19) зв'язок між геоцентричною широтою Ф та геодезичною B буде наступним

Для подальшого викладу нам будуть необхідні ще наступні залежності, що легко отримуються із (2.19)

cosB

cosu 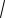1 e2 sin2 B ,

(2.21)

Якщо ввести позначення

то формули (2.21) будуть мати наступний вид

57

Розділ 2. Геометрія земного еліпсоїда

Із формули (2.24) з врахуванням (2.22) та зв'язку між ексцентриситетами (перша формула із 2.5) отримаємо вираз для V у функції геодезичної широти B

Функції V та W називають ще основними сфероїдними функціями геодезичної широти.

У сфероїдній геодезії часто використовується позначення

2.3.2. Зв’язки між різними видами координат.

X rcosL,

Y rsin L,

Z z,

та отриманих співвідношень (2.16), існують прості математичні залежності

58

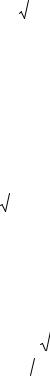
Розділ 2. Геометрія земного еліпсоїда

Радіус-вектор еліпсоїда re визначається із (2.17).

Обернені залежності, на основі (2.28), будуть мати наступний вид

Між просторовими прямокутними координатами X,Y,Z , приведеною широтою и та геодезичною довготою L на основі формул (2.10) та отриманих співвідношень між великою та малою півосями (див. третю формулу (2.5)), існують наступні залежності

X 2 Y 2

59

Розділ 2. Геометрія земного еліпсоїда

Враховуючи співвідношення (2.20) та (2.30), для поверхневих еліпсоїдних координат B,L та декартових X,Y,Z формули зв'язку мають вид

видно із подальшого викладу (параграф 2.4), це є рівняння для радіуса кривини першого вертикалу заданої точки на поверхні еліпсоїда у функції геодезичної широти. Остаточно, формули зв’язку будуть наступними:

Обернені залежності будуть мати наступний вид

Перша формула (2.33) отримана простим перетворенням (шляхом ділення другої формули (2.32) на першу). Друга

60

Розділ 2. Геометрія земного еліпсоїда

формула (2.33) отримана наступним чином. Із перших двох формул (2.32) отримаємо

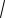X 2 Y 2 N cosB.

Поділивши третє рівняння (2.32) на отримане, дістанемо остаточно друге рівняння (2.33).

Зв’язок між геодезичними координатами B,L,H та

Спроектуємо висоту H (див.рис.1.3) на відповідні осі (рис.1.4). Тоді проекції висоти будуть виражені залежностями

X H cosBcosL,Y H cosBsinL,Z H sinB.

Або

Обернені залежності будуть мати наступний вид tgL YX ,

tgBi 1 Z btgBi , i 12, ...,n. (2.35) R c tg2 Bi

tgB1 ZR ,

61

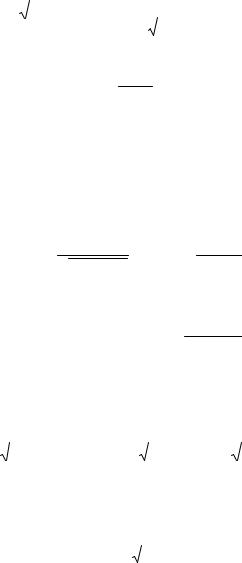
Розділ 2. Геометрія земного еліпсоїда

H sinZB (1 e2 )N.

Вираз для обчислення довготи L знаходимо аналогічно (2.33), а обчислення широти B , як видно із (2.35) вимагає застосування процесу наближень. Формула для B отримана наступним чином. На основі рівнянь (2.34), після нескладних перетворень, можемо отримати

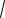X 2Z Y 2 tgB 1 Ne2 NH ,

а також

( N H )cosB 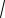X 2 Y 2 .

Тоді

або

Поділимо чисельник і знаменник у другому доданку (2.36) на cosB і в результаті перетворень отримаємо

62