Савчук підручник

Із наведених співвідношень отримаємо диференційні рівняння

а також формули для визначення і m

Диференційні рівняння (4.3) є тими умовами, які повинні задовільняти функції (4.1) при конформному зображенні еліпсоїда на площині.

Як вже було зазначено, точкова відповідність між поверхнею еліпсоїда і площиною повинна бути взаємною, тобто повинні існувати і зворотні функції

Умови, яким повинні задовільняти ці функції при конформному зображенні, визначаються наступними диференційними рівняннями

119

Рівняння (4.3) і (4.7) - основні рівняння конформного перетворення координат. Інтегрування їх виконується при початкових умовах, які задаються при зображенні еліпсоїда на площині чи навпаки.

В проекції Гаусса осьовий меридіан зображується прямою лінією, що приймається за вісь x з масштабом m=1, тобто для точок осьового меридіана абсциси рівні дугам меридіана

від екватора, а ординати - нулю. Якщо позначити дуги меридіана від екватора до точки заданої широти через X, то для точок осьового меридіана при l=0 отримаємо

Крім того, додатнім значенням l повинні відповідати додатні значення y і від’ємним l - від’ємні y; додатнім і від’ємним l відповідають тільки додатні значення x (для північної півкулі Землі). Ці умови і визначають проекцію Гаусса.

4.4. Перетворення полярних координат.

Одне із застосувань геодезичної лінії полягає в тому, що з її участю можна на поверхні еліпсоїда створити систему координат, в якій положення пунктів визначається довжиною геодезичної лінії s та кутом, що відраховується від заданого вихідного напряму. Якщо цей напрям збігається з меридіаном, то друга координата - кут, буде азимутом геодезичної лінії - A. Така система координат на еліпсоїді, аналогічна полярній системі координат на площині (довжина прямолінійного відрізка d та дирекційний кут ), називається п о л я р н о ю г е о д е з и ч н о ю.

Поскільки математичне опрацювання результатів геодезичних вимірювань значно простіше виконується на площині, ніж на еліпсоїді, то необхідно здійснити перетворення

120

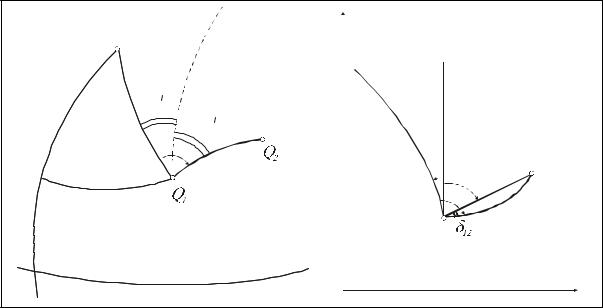
систем полярних координат, тобто знайти формули переходу від полярних координат s і A на еліпсоїді до відповідних їм координатам d і на площині.

Нехай Q1P меридіан, що проходить через т. Q1 (рис.4.3 а)); Q1T дотична до еліпсоїда і паралельна площині осьового меридіана. Кут між напрямом меридіана Q1P і дотичною Q1T називається геодезичним зближенням меридіанів в т. Q1 . Кут в т. Q1 між напрямом меридіана Q1P і геодезичною лінією Q1Q2 є геодезичний азимут А12 цієї лінії; кут в т. Q1 між напрямом дотичної Q1T і напрямом геодезичної лінії Q1Q2 є геодезичний дирекційний кут 12. Для поверхні еліпсоїда має місце очевидна

На рис. 4.3 б) : точки q1 і q2 зображення точок Q1 і Q2 поверхні еліпсоїда; ор вісь абсцис, зображення осьового меридіана ОР; q1n зображення меридіана Q1P; крива q1q2 зображення геодезичної лінії Q1Q2, d хорда, що стягує цю криву між точками q1 і q2. Кут між координатною лінією y = const і зображенням меридіана q1n називається зближенням меридіанів на площині; відраховується він від лінії y = const, тобто лінії, паралельної осі абсцис, в напрямі проти ходу годинникової стрілки. Напрямний кут 12, відрахований від координатної лінії у = const за годинниковою стрілкою до заданого напряму до хорди q1q2називається дирекційним кутом на площині. Кут 12 між дотичною до кривої q1q2 в т. q1 і хордою d називається поправкою за кривину зображення геодезичної лінії на площині або р е д у к ц і є ю н а п р я м у; відраховується він від дотичної до кривої за ходом годинникової стрілки до хорди. На площині має місце рівність

Згідно формули (4.2) для визначення довжини кривої S (зображення геодезичної лінії на площині) необхідно знайти інтеграл

121

кривину зображення геодезичної лінії, причому перша з них вводиться в напрям лінії S, а друга - в її довжину. В загальному випадку ці залежності складні, але для редукційних задач геодезії, що виникають при переході з еліпсоїда на площину, можна вивести наближені формули, які цілком задовільняють практичні вимоги.

122

4.5. Формули проекції Гаусса-Крюгера 4.5.1. Формули для обчислення координат

а) плоских прямокутних x,y за геодезичними B,l

При малій величині різниці довгот l L L0 залежність між плоскими прямокутними

координатами і геодезичними координатами для симетричних проекцій, якою є проекція Гаусса-Крюгера можна представити у вигляді наступних степеневих рядів:

де

B

X MdB,

0

а коефіцієнти в цих рядах є функціями тільки геодезичної широти B .

Характерною особливістю рівнянь (4.15) є залежність абсциси від членів парної степені різниці довгот, а ординати - тільки від непарної степені цієї різниці. Такі рівняння ще називають рівняннями симетричних проекцій. Для таких проекцій дві точки еліпсоїда, що мають одинакову широту і одинакову за абсолютною величиною різницю довгот l L L0 ,

після їх зображення на площині будуть мати одинакову абсцису та одинакову за абсолютною величиною ординату.

Знайдемо значення коефіцієнтів рівнянь (4.15).

Поскільки проекція має бути конформною, то поставимо вимогу, щоб рівняння зображення (4.15) задовільняли умови конформного зображення (4.3).

Підставимо в рівняння (4.3) часткові похідні рядів (4.15) . Тоді отримаємо

Із порівняння між собою в цих рівностях коефіцієнтів при одинакових степенях l , знайдемо

З цих формул видно, що для отримання кожного наступного коефіцієнта необхідно знайти похідну попереднього коефіцієнта. Враховуючи, що

123

Довжину дуги меридіана X від екватора до даної точки з широтою B можна обчислити за формулою (2.50)

де коефіцієнти A0,A2,A4,A6, що визначаються через параметри прийнятого еліпсоїда (див. ф- лу (2.50 ), для еліпсоїда Красовського мають наступні значення:

Формули (4.15) разом з (4.16)-(4.18) мають високу точність (до 0.001 м в x і y ) та

можуть застосовуватись для різниці довгот l 3 4o , тобто для системи шестиградусних зон. Щодо триградусних зон, то ці формули можна спростити, а саме: в формулі для x можна

124

Якщо виникає необхідність обчислення координат x і y з меншою точністю,

наприклад, до 1 м, то формули (4.19) з врахуванням коефіцієнтів для еліпсоїда Красовського можна спростити, а саме

аргументи B,l при цьому потрібно виразити в радіанах.

б) геодезичних B,l за плоскими прямокутними x,y

Щоб отримати формули для обчислення геодезичних координат за плоскими прямокутними координатами, представимо функції (4.6) у вигляді рядів за степенями ординати y, вважаючи її малою величиною. Для симетричних проекцій зображень ці ряди

будуть мати вигляд

Qx (рис.4.4).

x

Рис.4.4

Bx A0 x A2 sin(2A0 x) A4 sin(4A0 x) A6 sin(6A0 x),

де коефіцієнти A0 , A2 , A4 , A6 для еліпсоїда Красовського будуть мати наступні значення

125

A0 1.5704606433 10 7 ,

A2 2.5184637 10 3 ,

A4 3.7002 10 6 ,

A6 7.4 10 9 ,

а коефіцієнти рядів (4.20) будуть тоді функціями широти Bx .

Перейдемо до визначення коефіцієнтів в рядах (4.20). Підставимо в рівняння (4.7) часткові похідні рядів (4.20), де замість аргумента x будем брати аргумент X . Тоді отримаємо

Із порівняння між собою в цих рівностях коефіцієнтів при одинакових степенях y , знайдемо

....

Для знаходження всіх необхідних коефіцієнтів застосовуємо послідовне диференціювання по довжині дуги меридіана X , враховуючи при цьому, що

Остаточні значення коефіцієнтів рядів (4.20) мають наступний вигляд

126

Обчислені таким чином геодезичні координати будуть виражені в радіанній мірі. Точність цих формул така, що вони забезпечують 00001."в координатах B,l при розміщені точки на краю шестиградусної зони.

Аналогічним чином можна знайти вираз для обчислення зближення меридіанів за плоскими прямокутними координатами, тільки при цьому за вихідну беруть другу формулу

(4.8)

Приведемо остаточну формулу для зближення меридіанів у функції плоских прямокутних координат

127

У формулах (4.24) і (4.25) не враховано члени з e'4 . Точність приведених формул забезпечує обчислення в 0001.".

Знак зближення меридіанів співпадає зі знаком різниці довгот l або знаком y , тобто

для точок, які розташовані на схід від осьового меридіану, зближення меридіанів завжди буде додатнім, а на захід від нього - від’ємним.

4.5.3. Формули для обчислення масштабу проекції

Для знаходження формули масштабу зображення скористаємось формулою (4.5), яку представимо у вигляді

Як видно із даної формули, при l 0, тобто на осьовому меридіані, масштаб проекції рівний одиниці. При віддалені від осьового меридіана на схід і на захід значення масштабу швидко зростає.

Для отримання формули масштабу зображення у функції плоских прямокутних координат скористаємось другою формулою (4.19), яку, з прийнятими вище обмеженнями, запишемо

Застосовуючи формули обертання ряду для l cosB , знайдемо

звідки з прийнятою точністю

128