Савчук підручник

Розділ 3. Розв'язування геодезичних задач

раціональні прийоми, що дозволяли перетворювати формули для їх широкого практичного застосування. Вкажемо лише на два з них, що мали широке практичне використання при опрацюванні геодезичних мереж 1-го класу: метод допоміжної точки Шрейбера та метод середніх аргументів Гаусса.

В зв’язку з широким впровадженням комп’ютерної техніки на даний час можна вважати, що найбільш оптимальним шляхом розв’язування головних геодезичних задач є використання чисельних методів інтегрування диференційних рівнянь (3.27) і (3.28). Одним із найефективніших чисельних методів для вказаної задачі є метод Рунге-Кутта четвертого порядку. Детальніше про цей шлях буде розглянуто в п.3.6.4.

в) в просторі

Для розв’язування головних геодезичних задач в просторі використовують системи просторових декартових (X, Y, Z), геодезичних (B, L, H) та топоцентричних горизонтальних - декартових (x’, y’,z’) та полярних (A, z,D) координат і зв’язки між ними (див. розділи 1 і 2).

Пряма геодезична задача формулюється наступним чином. Задані геодезичні координати B1,L1,H1 початкової точки Q1 і топоцентричні полярні координати z12, A12, D точки Q2 відносно початкової точки Q1. Необхідно визначити геодезичні координати B2,L2,H2 точки Q2.

Поставлену задачу розв’язують в такій послідовності: а) за формулами зв’язку (2.32) обчислюють просторові декартові координати X1,Y1,Z1 точки Q1;

б) обчислюють елементи матриці перетворення координат A1 за формулою (2.37).

в) використовуючи формули (2.34), обчислюють топоцентричні декартові координати x2’,y2’,z2’;

г) за формулою (2.36) обчислюють декартові координати

X2,Y2,Z2 точки Q2;

д) для переходу до геодезичних координат B2,L2,H2 точки Q2 використовують формули зв’язку (2.33).

Обернена геодезична задача . Задані геодезичні координати B,L,H двох точок Q1 та Q2. Необхідно знайти

112

Розділ 3. Розв'язування геодезичних задач

топоцентричні полярні координати z12, A12, D точки Q2 відносно початкової точки Q1.

Для розв’язування поставленої задачі можна застосувати таку схему:

а) від геодезичних координат B,L,H точок Q1 та Q2 за формулами (2.32) переходять до декартових Xi,Yi,Zi (де і=1,2); б) обчислюють елементи транспонованої матриці перетворення

в) за формулою (2.38) обчислюють топоцентричні декартові координати xi’,yi’,zi’ (і=1,2) точки Q1 відносно точки Q2 і навпаки.

г) топоцентричні полярні координати z12, A12, D точки Q2 відносно початкової точки Q1 і z21, A21, D точки Q1 відносно точки Q2 обчислюють за формулами (2.35).

Приведені вище схеми можна використовувати також і для розв’язування головної геодезичної задачі між точками на поверхні еліпсоїда. Для цього в цих формулах достатньо прийняти H1=H2=0. Розв’язком при цьому, наприклад, в оберненій геодезичній задачі будуть азимути прямого і оберненого нормальних перерізів та довжина хорди цих перерізів.

113

Розділ 3. Розв'язування геодезичних задач

3.5. Диференційні формули.

Диференційні формули встановлюють залежність між малими (диференційними) змінами координат початкової і кінцевої точок відповідної лінії (дуги великого кола на сфері, геодезичної лінії на еліпсоїді, хорди в просторі), її довжини та азимутів.

Застосування диференційних формул пов’язано, в основному, з розв’язуванням задач з переобчислення геодезичних координат на поверхні земного еліпсоїда чи геоцентричних прямокутних в просторі у випадках зміни вихідних координат, а також аналогічних задач у випадку зміни (уточнення) розмірів відлікового еліпсоїда. Особливо це може стосуватися задач, що виникають при поєднанні пунктів, координати яких віднесені до референцних та загальноземного еліпсоїдів та визначені різними методами (класичними і супутниковими, наприклад).

Диференційні формули дозволяють значно скоротити обчислювальну роботу, яка вимагається при подібному переобчислені вже врівноважених координат всіх опорних геодезичних пунктів. Це виявляється можливим тому, що повторне обчислення координат замінюється обчисленням незначних поправок до вже відомих координат пунктів. Такими формулами для обчислення поправок в координати та азимути напрямів і є диференційні формули.

Крім вищеназваних, диференційні формули можна використовувати і в інших задачах. Так в п. 3.6. буде наведена схема розв’язування оберненої геодезичної задачі, одним із важливих етапів якої є застосування диференційних формул для довжини геодезичної лінії та азимута цієї лінії.

3.5.1. диференційні формули для геодезичної лінії.

Сім змінних B1, L1, B2, L2, s, A1, A2 геодезичної лінії зв’язані між собою складною залежністю, котра визначається формулами розв’язування головних геодезичних задач. З цих

114

Розділ 3. Розв'язування геодезичних задач

семи змінних чотири є незалежними; від них залежать решта три.

Зміну трьох залежних змінних представимо у вигляді повних диференціалів

Ці рівняння показують, як змінюється довжина геодезичної лінії та її азимути у випадку, якщо кінці цієї лінії отримують деякі малі зміщення, котрі виражені диференціалами координат. Рівняння (3.37) приймаються за вихідні співвідношення, з яких потім знаходять інші залежності між цими диференціалами.

Часткові похідні можна знайти, застосовуючи при цьому два підходи. Перший - менш строгийполягає в тому, що при виводі формул користуються геометричним представленням часткових диференціалів, що складають праві частини рівнянь (3.37), а другий - строгий - в тому, що часткові похідні знаходять диференціюванням за відповідними змінними рівнянь, що використовують для розв’язування головних геодезичних задач. В курсах вищої геодезії [1,5,7] ці підходи розглядаються детальніше. Ми обмежимося лише готовими формулами, які будемо класифікувати за впливами:

зміни широти B2 на величини s, A1, A2 при постійній величині довготи L2 та незмінному положенні початкової точки Q1

115

Розділ 3. Розв'язування геодезичних задач

Тут m - приведена довжина геодезичної лінії. Для більшості

s

випадків її можна обчислити за формулою: m Rsin R .

зміни довготи L2 на величини s, A1, A2 при постійній величині широти B2 та незмінному положенні початкової точки Q1

Аналогічні вирази будуть і в тому випадку, коли кінцева точка Q2 залишається в незмінному положенні, а зміщення отримала початкова точка Q1 . Різниця буде лише в тому, що у формулах (3.38) та (3.39) поміняються місцями індекси 1 і 2. Повні диференційні формули запишуться в цьому випадку в наступному виді

зміни широти B1 на величини B2, L2, A2 при постійній величині довготи L1 , азимута A1 та довжини геодезичної лінії s

116

Розділ 3. Розв'язування геодезичних задач

зміни довжини геодезичної лінії s на величини B2, L2, A2 при постійній величині широти B1, довготи L1 , азимута A1

зміни азимута A1 на величини B2, L2, A2 при постійній величині широти B1, довготи L1 та довжини геодезичної лінії s

117

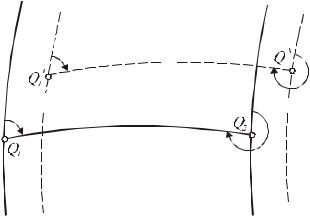
Розділ 3. Розв'язування геодезичних задач

Рис. 3.5 дає геометричне представлення про величини, що входять в диференційні формули (3.38)- (3.43).

Рис. 3.5

Всі наведені вище формули є наближеними, поскільки в них не прийняті до уваги диференціали другого і більш вищих порядків. Тому вони тим точніші, чим менші величини диференціалів незалежних змінних.

3.5.2. диференційні формули для довільної точки простору.

Встановимо залежності між малими змінами просторових декартових і геодезичних координат довільної точки в просторі. В загальному вигляді ці залежності можна записати

118

Розділ 3. Розв'язування геодезичних задач

Часткові похідні в цих залежностях можна знайти із рівнянь (2.32)

Для цього попередньо визначимо похідні двох функцій

dBd (N cosB) dNdB cosB NsinB, dBd (NsinB) dNdB sinB N cosB.

Враховуючи, що

а радіус кривини меридіана M можна записати у вигляді

(1 e2 )

M (1 e2 sin2 B) N,

то для наведених функцій матимемо

119

Після цього можна легко знайти часткові похідні, наприклад

Після підстановки похідних в попередні залежності, отримаємо

де матриця перетворення P має елементи

Звідси можна знайти і обернені залежності

120

де P' - транспонована матриця Р.

3.5.3. диференційні формули для системи геодезичних координат.

Зміна розмірів еліпсоїда і його орієнтування відносно фізичної поверхні Землі викликає зміну геодезичних координат всіх точок навколишнього простору.

Формули, за якими визначаються малі зміни геодезичних координат B, L, H точок земної поверхні або навколоземного простору, що викликані малими змінами розмірів еліпсоїда і його паралельним зсувом в просторі носять назву диференційних формул системи геодезичних координат.

Нехай деякий еліпсоїд заданих розмірів (a, ) встановлений відносно земної поверхні так, що вісь обертання його паралельна до осі обертання Землі, а центр еліпсоїда незначно віддалений від центра інерції Землі.

Якщо тепер змінимо форму і розміри еліпсоїда: велику (екваторіальну) піввісь на величину da, а стиснення на величину d , то, відповідно, зміняться при цьому і геодезичні координати B,L,H всіх точок простору, проте прямокутні координати X,Y,Z цих точок залишаться попередніми, поскільки не змінилося положення осей координат.

Здійснивши паралельне зміщення еліпсоїда в просторі разом з осями координат OXYZ , отримаємо додаткові зміни геодезичних координат. Зміняться на цей раз і прямокутні координати всіх точок (в результаті переносу початку координат) на величини dx, dy, dz.

Вказані зміщення (перехід від одної системи геодезичних координат до другої) можна проілюструвати геометрично (рис. 3.6).

121