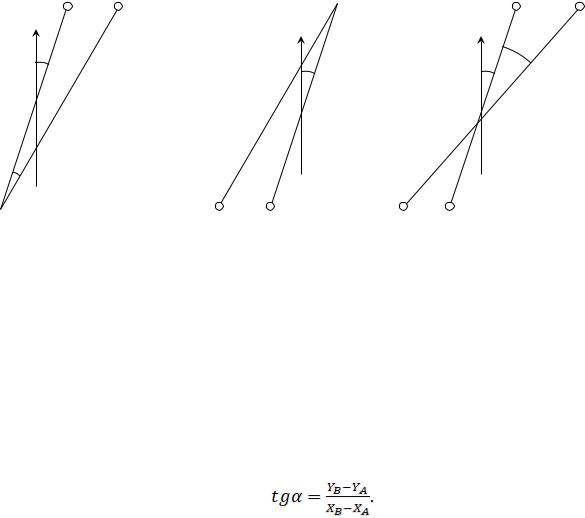
відомі з курсу “Топоґрафії” графічні методи розв’язування цієї задачі, запропоновані Бесселем, Леманом. Відомо також, що ця задача не має розв’язку, якщо шуканий пункт розташований на колі, що проходить через три пункти з відомими координатами. Уже цей факт вимагає виконувати вимірювання з шуканого пункта не на три, а мінімум на чотири відомих пункти. Тоді одноразова обернена засічка стане в багаторазовою оберненою засічкою. Така засічка, як і багаторазова пряма засічка, дає можливість декілька разового визначення координат шуканої точки. Тобто також постає питання визначення
найімовірніших поправок δX та δY до наближених координат Xo , Yo . Визначення δX та δY
виконують по способу найменших квадратів. Для цього застосовують диференційні формули дирекційних кутів.
|
3.3.5. Диференційні формули дирекційних кутів |
|
|||||
Відрізок |
AB задано |
координатами його |
кінців |
A(X A ,YA ), |
B(X B ,YB ) , |
а його |
|
дирекційний кут – α . Точка |
A не змінює свого положення. У ній установлюють теодоліт, |
||||||
коли виконують |
пряму кутову засічку. |
Внаслідок похибок вимірювання кута |
точка B |
||||
змінить своє положення, і її координати |
будуть |
X B +dX B ; |
YB +dYB . |
Тоді дирекційний кут |
|||
також змінить своє значення на dα . Формули, що виражають такий зв’язок між змінами координат та змінами дирекційних кутів називають диференційними формулами дирекційних кутів.
І |
ІІ |
B |
|
B' |
|
|
|
|
|
(XB+dXB) |
|
α |
(YB+dYB) |
|
|
dα
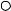(теодоліт) A відома
(XA,YA) “тверда”
відома B
“тверда”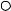 
dα
α
A' A шукана
(теодоліт)
(XA+dXA) (XA,YA) (YA+dYA)
ІІІ |
|
|
B (XB,YB) |
B' |
|
шукана |
(XB+dXB) |
|
(теодоліт) |
||
(YB+dYB) |
||
|
||
dα |
|
|
α |
|
(XA+dXA) |
|
|
(YA+dYA) |
|
|
A' |
A |
шукана |
|
(XA,YA) |
(теодоліт) |
Рис. 3.18. До пояснення суті диференційних формул дирекційних кутів.
В іншому випадку, “шукана” точка A змінюватиме свої координати. На ній установлено теодоліт. Точка B – відома і не змінює координат. Цей випадок відповідає оберненій кутовій засічці.
На останок, загальний випадок, коли змінюються, координати як точки A , так точки B Теодоліт встановлюється вобох точках. Цей випадок відповідає прокладанню ходів.
Виведемо формули для двох випадків (пряма та обернена засічка), а з них загальну
формулу. Скористаємося відомою формулою (3.75) |
|
. |
(3.90) |
20 |
|
Випадок I (пряма засічка). Продиференціюємо цю формулу, вважаючи, що змінними
є координати тільки точки B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
(3.91) |
||
Оскільки: X B − X A = S cosα ; YB −YA = S sinα , формулу(3.91) запишемо так: |
|
|
|||||||||||||||||
1 |
dα′′ = |
S cosα d YB −S sinα dX B |
. |
(3.92) |
|||||||||||||||
|
cos2 α |
|
|
|
|
|
|
|
|||||||||||
|
ρ′′ |
|
|
S 2 cos2 α |
|
|
|||||||||||||
Скоротивши обидві частини рівняння (3.92) |
на |
cos2 α , та чисельник і знаменник |
|||||||||||||||||
правої частини на S, матимемо для dα′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
dα′′ = ρ′′ |
cosα |
|
dYB − ρ′′ |
sinα |
dX B . |
(3.93) |
||||||||||||
|
|
|
|
||||||||||||||||
Введемо позначення: |
|
S |
|
|
|
|
|
|
|
S |
|
|
|||||||
(a)= −ρ′′sinα |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
(3.94) |
||||||||||||||
|
|
(b)= ρ′′cosα |
. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
З урахуванням цих позначень формула (3.93) виглядатиме |
|
|
|||||||||||||||||
|
|
dα = (a)dX |
B |
+ |
|
(b) |
dY . |
(3.94) |
|||||||||||
|
|
|
|
||||||||||||||||
|
|
|
S |
|
|
S |
B |
|
|
||||||||||
Для другого випадку (обернена засічка), |
коли |
змінюються координати точки |
A . |
||||||||||||||||
Якщо розглядати формулу( 3.90), |
не важко зауважити, що координати точки A |
в |
цій |
||||||||||||||||
формулі відрізняються від координат точки B знаками. Тому для другого випадку остаточну |
|||||||||||||||||||
формулу можна записати за аналогією з формулою (3.94) |
|
|
|
|
|
||||||||||||||
|
|
dα = − |
(a) |
dX |
A |
− |
(b)dY . |
(3.95) |
|||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
S |
|
|
|
S |
A |
|
|
|||||||
І, для загального випадку (хід), коли змінюються координати точок B і A, матимемо формулу
(3.96)
Як бачимо з ц их формул, щоб знайти зміни дирекційних кутів dα , необхідно крім змін координат точок знати довжини ліній Si та коефіцієнти (a)i і (b)i .
3.3.6. Обернена багаторазова кутова засічка
Нехай на шуканому пункті P виміряно більше ніж два кути на пункти з відомими координатами. Спочатку використовуючи два кути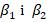 
та координати трьох пунктів
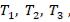розв’язують обернену одноразову засічку і обчислюють приблизні координати пункта P0 Xo та Yo . Маючи надлишковий вимір для поданого рис. 3.19, кут на четвертий
пункт, виконують врівноважувальні обчислення для знаходження поправок у наближені координати пункта P.
.
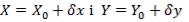T1
P |
β1 |
T2 |
|
β2 |
|
|
|
21
β3 
T3
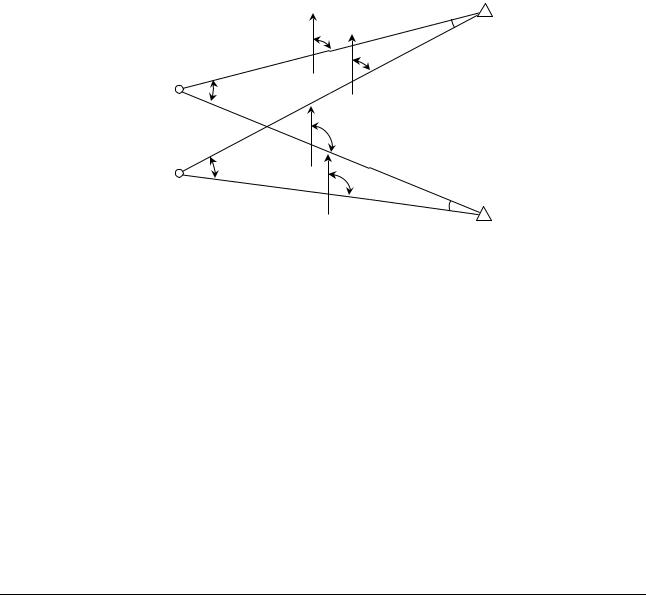
Рис. 3.19. Багаторазова кутова обернена засічка
Для складання рівнянь, на основі яких можна буде знайти поправки δX та δY в наближені координати точки, скористаємось рисунком 3.20, на якому зображені дві вихідні точки Ti та Ti+1 ; точка Po , з наближеними координатами Xo та Yo , та точка P, найімовірніші
координати якої X та Y поки що невідомі.
На основі рис. 3.20 запишемо очевидні, приведені нижче рівняння, і в іднімемо від першого рівняння друге:
βі =αі+1 −αі |
(1) |
|
|
βоі =αоі+1 −αоі |
|
(2). |
(3.97) |
βі −βоі =αі+1 −αі −αоі+1 +αоі
|
|
dαi |
Ti |
|
|
αi |
|
|
Si |
α0i |
|
P |
βi |
Si+1 |
|
X Y |
|
||
|
αi+1 |
|
|
|
S0i |
|
|
P0 |
β0i |
α0i+1 |
|
|
|
|
|
X Y |
S0i+1 |
dαi+1 |
Ti+1 |
|
|
|
Рис. 3.20. Зміни дирекційних кутів та координат під час елементарного переміщення шуканої точки P .
Рівнянь (3.97) можна записати стільки, скільки виміряних кутів βi . З цього ж рисунка,
у свою чергу, можна записати: |
(3) |
|
αі+1 =αоі+1 +dαi+1 |
|
|
αi =αoi +dαi |
(4). |
(3.98) |
Замінивши у рівнянні (3.97) αі+1 та αі їхніми значеннями, у відповідності з (3) та (4), |
||
системи (3.98) отримаємо |
|
|
βі − βоі =αоі+1 + dαi+1 −αoi − dαi −αoi+1 +αoi , |
|
|
або, після скорочення, матимемо: |
|
|
βi −βoi = dαi+1 −dαi . |
|
(3.99) |
Це рівняння можна було б записати також на основі рисунка, оскільки під час переміщення точка Po в точку P кут βoi зміниться на βi , а різниця зміни дирекційних кутів
dαi та dαi+1 перетвориться в нуль. У рівнянні (3.99) βoi знаходять, як різницю, відомих із
22
розв’язування одноразової засічки, дирекційних кутів αоі+1 та αоі ; врівноважений кут βi
поки що невідома величина. У рівнянні (3.99) немає виміряного кута. Позначимо виміряний кут через βi′ і введемо його в рівняння (3.99), віднявши і додавши його улівій частині
рівняння. Отримаємо
βі − βі′+ βі′− βоі = dαi+1 − dαi . |
(3.100) |
Позначивши відому різницю βoi − βi′= li , а невідому |
βi − βi′= vi , рівняння (3.100) |
набуде вигляду рівняння похибок |
|
vi = dαi+1 −dαi +li . |
(3.101) |
Замінимо в формулі (3.101) зміни дирекційних кутів dαi+1 та dαi |
змінами координат |
|||||||||||||||||||||||||
відповідно з отриманою диференційною формулою (3.95), (обернена засічка) |
||||||||||||||||||||||||||
v |
= (ai )dX |
+ |
|
(bi |
) |
dY − |
(ai+1 ) |
dX − |
|
(bi+1 ) |
dY +l . |
(3.102) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
i |
|
Soi |
|
|
|
|
|
Soi |
Soi+1 |
|
|
|
|
|
|
i |
|
|||||||||
Або |
|
|
|
|
|
|
|
|
|
|
Soi+1 |
|
||||||||||||||
|
|
(a ) |
|
(a |
|
) |
|
(b ) |
|
(b |
|
|
) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
vi |
= |
|
|
i |
|
− |
|
i+1 |
|
|
dX + |
|
i |
|
− |
|
i |
+1 |
dY +li . |
(3.103) |
||||||
|
|
S |
|
|
|
S |
|
S |
||||||||||||||||||
|
|
S |
oi |
|
oi+1 |
|
|
|
oi |
|
oi+1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Позначимо:
|
|
|
(аі )− |
ai+1 |
; |
|
|
|
(bi ) |
|
(bi+1 ) . |
|||||
А |
= |
|
B |
= |
|
− |
||||||||||
|
|
|
|
|||||||||||||
і |
|
|
|
S |
|
|
i |
|
S |
|
|
S |
|
|
||
|
|
S |
oi |
oi+1 |
|
|
|
|
oi |
oi+1 |
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
Тодіотримаємо скорочений, кінцевий вигляд рівнянь похибок
vi = Aidx + Bidy +li .
Таких рівнянь можна записати стільки, скільки виміряних кутів:
v1 = A1dx + B1dy +l1 |
|
|
|||
v |
2 |
= A dx + B dy +l |
2 |
|
|
|
2 |
2 |
|
||
v3 = A3dx + B3dy +l3 |
|
||||
. |
|||||
..................................... |
|||||
v |
|
= A dx + B dy +l |
|
|
|
n |
n |
|
|||
|
n |
n |
|
||
(3.104)
(3.105)
(3.106)
Рівняння (3.106) є параметричними рівняннями поправок. За умови [vv] = min, матимемо стільки нормальних рівнянь, скільки невідомих. У нас дві невідомі dx та dy . Тому
буде два рівняння:
(3.107)
Розв’язуючи рівняння способом (Крамера) визначників знайдемо невідомі dx та dy .
dx = |
[AB][Bl]−[BB][Al] |
[AA][BB]−[AB][AB] |
|
|
. |
dy = |
[AB][Al]−[AA][Bl] |
|
|
|
[AA][BB]−[AB][AB] |
Оскільки Si в км, а ρ′′ приймемо рівним 20,6265, тоді десятих частках метра (в дециметрах). Томуостаточно:
X = Xo +0,1dx .
Y = Yo +0,1dy
(3.108)
dx та dy виражатиметься в
(3.109)
23