
- •2.1. Джерела похибок вимірювання горизонтальних кутів
- •2.5. Розрахунок допустимої величини випадкової похибки на окреме джерело вимірювання горизонтальних кутів для ходу з ув’язаними кутами.
- •2.12. Способи зменшення похибок центрування і редукції. Триштативна система.
- •2.14.Похибки у вимірюванні кута через приладові похибки
- •3.1. Світловіддалемірна поліґонометрія.
- •3.1.1. Принцип вимірювання віддалі світловіддалеміром
- •3.1.3. Принцип роботи фазових світловіддалемірів
- •3.3. Попереднє опрацювання результатів польових вимірів в поліґонометрії
- •3.3.1. Попереднє опрацювання лінійних вимірювань
- •3.3.2. Редукування довжин ліній на рівень моря
- •3.2.3. Необхідна точність визначення радіуса Землі та висот пунктів для редукування ліній на рівневу поверхню.
- •3.2.5. Необхідна точність визначення радіуса Землі та значення ординати пунктів для редукування ліній з рівневої поверхні на площину у проекції Ґавсса-Крюґера.
- •3.3. Прив’язування поліґонометричних ходів.
- •3.3.1. Прив’язування ходів до близьких (недоступних) пунктів (знесення координат)
- •3.3.3. Пряма одноразова та багаторазова засічки
- •3.3.4. Обернена одноразова кутова засічка
- •3.3.5. Диференційні формули дирекційних кутів
- •3.3.6. Обернена багаторазова кутова засічка
- •3.3.7. Точність прямої та оберненої багаторазових кутових засічок
- •3.3.8. Точність прямої та оберненої одноразових кутових засічок
- •3.3.10. Лінійна геодезична засічка
- •3.3.11. Визначення координат двох пунктів за відомими координатами двох вихідних пунктів (задача Ганзена)
- •9. Розрахунок точності та допустимої довжини теодолітного ходу
- •10. Геометричне технічне нівелювання для створення знімальної основи топоґрафічного знімання
- •11. Триґонометричне нівелювання для створення висотної знімальної основи топоґрафічного знімання
- •12. Вимірювання зенітних відстаней. Вертикальна рефракція
3.3. Прив’язування поліґонометричних ходів.
Прив’язування поліґонометричних ходів до пунктів вищого класу (розряду), які є вихідними, виконують для визначення координат пунктів прокладуваного ходу. Є різні способи прив’язування залежно від розташування вихідних та визначуваних пунктів. Розглянемо деякі з них.
3.3.1. Прив’язування ходів до близьких (недоступних) пунктів (знесення координат)
Якщо на заданий вихідний пункт неможливо установити теодоліт (електронний тахеометр), тому що це якийсь шпиль чи хрест церкви. То для виконання такого прив’язування необхідно, закласти початковий пункт так, щоби із нього було видно не тільки близький пункт (наприклад, хрест церкви) з відомими координатами але, як мінімум, ще один пункт із відомими координатами.
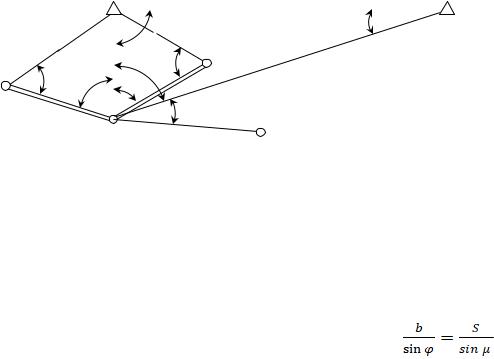
Нехай потрібно визначити координати пункта Р, що є початком ходу. Для цього спочатку потрібно визначити горизонтальну віддаль S (рис. 3.14) між точками T1 таP .
Для цього вимірюємо базис b1 та, для контролю b2 . Базиси є сторонами трикутників T1P A і T1 P B. Вимірюємо горизонтальні кути α , β , γ , ψ, ϕ, β1 .
Для досі згаданих трикутників, за теоремою синусів, можемо записати
|
|
S |
= |
|
b1 |
|
; |
|
S |
= |
|
b2 |
|
. |
|
(3.64) |
|
|
|
sinγ |
|
sin[180o −(α +γ )] |
|
sinψ |
sin[180o − |
(β +ψ )] |
|
||||||||
|
|
T1 |
(X1, Y1) |
|
|
|
|
b |
|
|
|
T2 (X2, Y2) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
S |
|
ψ |
|
B |
|
|
|
|
|
|
|
|
|
||
А |
γ |
|
ϕ |
b2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
α |
β |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
β1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
P (XP, YP) |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 3.14. Знесення координат із недоступної точки T1 |
на пункт поліґонометрії P. |
||||||||||||||||
На основі формул ( |
3.64) обчислюють два значення |
S1 та |
S2 . Обчислюють середнє |
||||||||||||||
значення S . |
|
|
|
|
|
|
лінії T1 - P . |
|
|
|
|
|
|
|
|||
Визначаємо дирекційний кут |
αT −P |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Для трикутника T1T2 P запишемо теорему синусів: |
|
|
|
Помилка! Закладку не визначено. |
. |
||
З формули (3.65) кут µ , дорівнюватиме: |
|
|
|
S sinϕ |
|
|
|
µ = arcsin |
|
. |
|
b |
|
||
|
|
|
|
Із цього ж трикутника обчислимо кут λ .
λ =180o −(µ +ϕ).
Далі обчислюємо дирекційний кут αT1 −P :
α(Т1 −Р ) =α(Т1 −Т2 ) + λ .
15
(3.65)
(3.66)
(3.67)
(3.68)

Тепер обчислимо координати X P , YP . |
|
|
|
|
|
|
|
|
|
|||
Знаючи координати точки T1 ( X1 , Y1 ), |
довжину лінії S та її дирекційний кут α(Т1 −Р ) і, |
|||||||||||
розв’язавши пряму геодезичну задачу, знайдемо шукані координати точки X P , YP . |
|
|||||||||||
|
∆Х = S cosα |
(Т1 −Р |
) |
|
|
|
||||||
|
|
|
|
|
|
|
|
(3.69) |
||||
|
∆У = S sinα |
|
|
|
|
|
. |
|
||||
|
(Т1 |
− |
Р |
) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
ХР |
= ХТ |
1 |
+ S cosα(T −P ) |
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
(3.70) |
|
Y |
|
= Y + |
S sinα |
|
|
|
. |
|||||
P |
(T1 |
− |
P ) |
|
|
|||||||
|
T1 |
|
|
|
|
|
|
|
|
|||
Тепер розв’язавши обернену геодезичну задачу отримаємо дирекційний кут αT2 −P , і
маючи кут β1 можемо обчислити дирекційний кут початкової лінії Р-1, прокладуваного ходу.
3.3.2. Точність прив’язування ходів до близьких недоступних пунктів
Запишемо одну із формул (3.64) визначення віддалі до недоступного пункту таким чином
(3.71)
Продиференціюємо ф-лу (3.71) по b , α і γ та перейдемо до с.к.п. Приймемо що похибки вимірювання кутів α та γ, однакові тобто 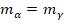 .
.
.
Приклад.
Нехай базис b = 40 м. С.к.п. вимірювання базиса 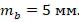 Віддаль S =70 м. С.к.п. вимірювання кутів для коротких сторін і високо розташованоїточки Т1
Віддаль S =70 м. С.к.п. вимірювання кутів для коротких сторін і високо розташованоїточки Т1 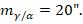
Нехай 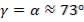 , а
, а 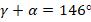 . Тоді Якщо S визначати із двох базисів
. Тоді Якщо S визначати із двох базисів
3.3.3. Пряма одноразова та багаторазова засічки
Якщо є можливість на всіх вихідних пунктах установити прилади, і з цих пунктів є видність на інші вихідні пункти, а початковий пункт прокладуваного ходу розташований на значній віддалі від вихідних пунктів, то прив’язування ходу виконують, зазвичай прямою кутовою засічкою.
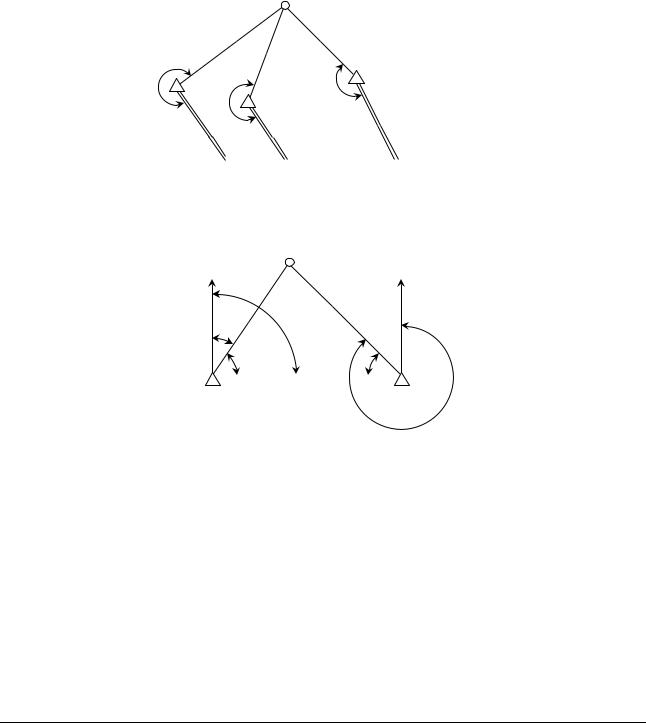
Якщо на всіх вихідних пунктах немає можливості установити прилади, і не з усіх пунктів є видність на інші вихідні пункти, а початковий пункт прокладуваного ходу розташований на значній віддалі від вихідних пунктів, то прив’язування ходу виконують, зазвичай оберненою кутовою засічкою. Нехай для визначення координат точки P (рис. 3.15)
з кожного з відомих пунктів T1 , T2 , T3 на точку P виміряні кути β1 , β2 , β3 між лініями з
відомими дирекційними кутами αA , αB , αC та напрямами на точку P . Це випадок коли між
сусідніми пунктами з яких вимірюють кути немає видності.
Маючи координати всіх трьох точок, три дирекційні кути та три виміряні кути можна визначити три значення X P та YP , комбінуючи точки з відомими координатами по дві: 1,2;
1,3; 2,3.
16
Визначення найімовірніших |
координат точки |
P( X |
P |
,Y ) |
за цими вимірюваннями |
називають прямою багаторазовою засічкою. |
|
P |
|
||
|
|
|
|
||
Проте, як це зрозуміло з досі сказаного, достатньо мати дві відомі точки, наприклад, |
|||||
T1 та T2 , щоб знайти координати |
шуканої точки X P |
та |
|
YP . |
Розглянемо рис. 3.16. У |
трикутнику T1 PT2 відомі три елементи. |
|
Це означає, |
що трикутник можна розв’язати та |
||||||||||||
знайти інші три елементи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S1 |
|
|
= |
|
|
в |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
sin β |
2 |
|
sin[180o − |
(β |
+ β |
2 |
)] |
|
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
(3.71) |
||
|
S2 |
|
|
|
|
|
|
в |
|
|
|
|
|
. |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
sin β1 |
|
sin[180 |
− |
(β1 + β2 )] |
|
|||||||||
|
|
|
|
||||||||||||
P
β1 |
β2 |
β3 |
T3 |
|
|||
|
T1 |
T2 |
|
|
|
|
|
|
αΑ |
αΒ |
αС |
|
|
||
|
A |
B |
C |
Рис. 3.15. Пояснення суті прямої багаторазової засічки.
|
|
P(XP,YP) |
|
|
|
|
x |
|
x |
|
|||
|
S1 |
S2 |
|
|
|
|
|
|
αΤ1− Τ2 |
|
|
|
|
αΤ1−P |
|
|
|
|
||
|
β |
|
β2 |
αΤ2−P |
||
|
|
|
|
|
||
|
|
|
|
|
||
T1 |
b |
T2 |
||||
|
||||||
|
|
|||||
X1,Y1 |
|
X2,Y2 |
|
|||
Рис. 3.16. До пояснення суті прямої одноразової засічки.
З формул (3.71) знайдемо довжини ліній S1 та S2 . Далі визначимо дирекційні кути цих ліній:
|
α(Т1 −Р) =α(Т1 −Т2 ) − β1; |
α(Т2 −Р) =α(Т2 −Т1 ) + β2 . |
|
(3.72) |
||||||||||||||||
Координати точки |
P( X |
,Y |
) можна визначити два рази із контролем |
обчислень (не |
||||||||||||||||
|
P |
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вимірювань): один раз, використовуючи точку T1 , а другий – точку T2 . |
|
|
||||||||||||||||||
X |
′ = |
X |
+ S cos |
α |
|
|
|
X |
′′ = X |
+ S |
2 |
cosα |
(T2 −P) |
|
|
|||||
|
P |
|
T1 |
1 |
|
|
(T1−P) |
; |
|
P |
T2 |
|
|
|
|
|
(3.73) |
|||
Y′ =Y |
+ S |
sinα |
|
|
|
|
Y′′ =Y |
+ S |
|
sinα |
|
|
. |
|||||||
(T1−P) |
|
|
2 |
(T2 −P) |
|
|
||||||||||||||
P |
|
T1 |
1 |
|
|
|
P |
T2 |
|
|
|
|
|
|
||||||
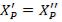 і
і 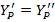 , мають бути рівні з точністю обчислень.
, мають бути рівні з точністю обчислень.
17
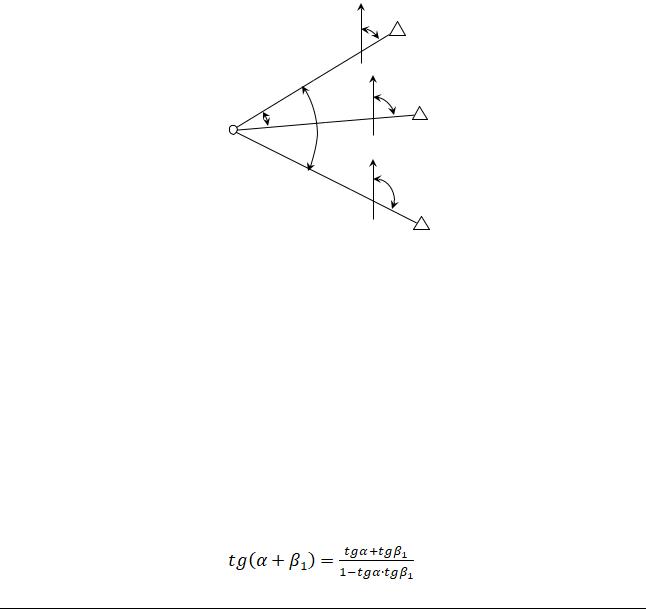
Визначення координат точки P за двома відомими точками та виміряними в цих точках кутами β1 та β2 , називають одноразовою, прямою кутовою засічкою.
Якщо виконані вимірювання необхідні для прямої, багаторазової засічки, тоді ця задача розв’язується так. Вибирають дві точки з відомими координатами, бажано так, щоб лінії візування на шукану точку P перетиналися під кутом, який найближчий до прямого.
Розв’язують одноразову пряму засічку й знаходять наближені координати точки P – Xo , Yo .
Потім, по способу найменших квадратів обчислюють найімовірніші поправки δX та δY до наближених координат, тобто знаходять:
ХР = Хо +δХ ; YP = Yo +δY . |
(3.74) |
Зрівноваження виконують аналогічно до описаного далі зрівноваження оберненої багаторазової засічки.
Зрозуміло, що такий розв’язок задач усуває необхідність декілька разів розв’язувати пряму, одноразову засічку.
3.3.4. Обернена одноразова кутова засічка
Потрібно визначити координати пункта P за виміряними двома кутами β1 та β2 із шуканого пункта, на три пункти T1 , T2 , T3 з відомими координатами (рис. 3.17).
Таку задачу називають оберненою одноразовою кутовою засічкою.
|
|
|
|
|
α |
T1 |
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
X1,Y1 |
|
||
|
|
|
|
|
|
α1 |
|
|
|
|
P |
β1 |
|
|
|
|
|
|
|
T2 |
|
|
|
|
|
|
|
|
|
X2,Y2 |
|
|
X,Y |
|
|
β2 |
|
|
|
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
α2 |
|
|
|
|
|
|
|
|
|
|
|
|
T3 |
|
|
|
|
|
|
|
|
|
|
X3,Y3 |
|
Рис. 3.17. Обернена одноразова засічка. |
|
|||||||||
Нехай координати пункта P(X ,Y ) |
обчислені. Тоді для визначення дирекційного кута |
|||||||||
α напряму P -T1 , можемо записати формулу |
|
|
Y1 −Y |
|
|
|
|
|
||
|
|
tgα |
= |
. |
|
|
|
(3.75) |
||
|
|
|
|
|
|
|||||
|
|
|
|
|
X1 − X |
|
|
|
|
|
Формулу (3.75) запишемо таким чином для кожного із трьох напрямів: |
|
|||||||||
Y −Y = (X |
|
− X )tgα |
|
|
|
|
||||
Y12 |
−Y |
= (X12 |
− X )tg(α + β1 ) . |
(3.76) |
||||||
Y |
−Y |
= (X |
3 |
− X )tg(α |
+ β |
2 |
) |
|
||
3 |
|
|
|
|
|
|
|
|
||
У системі рівнянь (3.78) є три рівняння і три |
невідомі – координати |
X , Y та |
||||||||
дирекційний кут α . Отже, система рівнянь розв’язується. |
|
|
|
|||||||
Єбагато способів розв’язування цих рівнянь. Подамо розв’язок цієї системи такий як
увсіх класичних підручниках.
Запишемо формулутанґенса суми кутів для другого рівняння системи (3.76)
. (3.77)
18

Помноживши чисельник і знаменник правої частини (3.77) на |
отримаємо |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.78) |
Підставимо (3.78) у друге рівняння системи (3.76) і, перемноживши всі члени |
|||||||||||||||||
отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.79) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поступимо аналогічно із третім рівнянням системи (3.76) |
|
|
|
|
|||||||||||||
Віднявши від (3.80) (3.79) отримаємо |
|
|
|
|
|
|
|
|
|
|
|
(3.80) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. (3.81) |
Із першого рівняння системи (3.76) знайдемо |
|
|
|
|
|
|
|
|
|
||||||||
|
|
, і підставимо у(3.81). Звівши подібні члени знайдемо |
|||||||||||||||
|
(Y2 −Y1 )ctgβ1 −(Y3 −Y1 )ctgβ2 +(X 3 − X 2 ) |
|
|||||||||||||||
tgα = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(3.82) |
(X |
2 |
− X |
1 |
)ctgβ |
1 |
−(X |
3 |
− X |
1 |
)ctgβ |
2 |
− |
(Y |
−Y ) |
|||
|
|
|
|
|
|
|
|
3 |
2 |
|
|
||||||
Знаючи α , визначимо дирекційні кути α1 та α2 двох інших напрямів (рис. 3.17):
α1 =α +β1 . |
(3.83) |
α2 =α + β2 . |
(3.84) |
Віднімемо від другого перше рівняння системи (3.76)
,
і визначимо абсцису
. (3.85)
Обчислення можна виконувати за цією формулою, або віднявши від обидвох частин рівняння (3.85) , після нескладних перетворень, отримаємо формулу яку подають у
підручниках |
|
(X2 − X1 )tgα −(Y2 −Y1 ) |
|
|
|
X = X2 |
+ |
. |
(3.86) |
||
|
|||||
|
|
tg(α + β1 )−tgα |
|
||
Аналогічно, якщо усистемі (3.76) віднімемо від третього перше рівняння, і розв’язуватимемо так, як описано досі, отримаємо
(3.87)
Знаючи X , обчислимо Y , скориставшись одним з рівнянь системи (3.76). Візьмемо перше та третє рівняння цієї системи і запишемо їх так:
,
. (3.88)
Для контролю отриманих дирекційних кутів, за остаточними координатами, обчислюють дирекційний кут 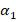
|
(3.89) |
Значення |
є остаточним, і якщо воно відрізняється від обчисленого за формулою |
(3.83) на 180°, то |
і теж змінюють на 180°. |
Обернена одноразова засічка має широке застосування в геодезичній практиці, оскільки для визначення координат пункта достатньо виміряти 3 кути на шуканому пункті. Існує більше ста методів аналітичного та графічного розв’язання цієї задачі. Студентам
19
