1.4.3. Распределение хи-квадрат

Определение. Пусть случайные величины ξ₁, ξ₂, …, ξ_n — независимы, и каждая из них имеет стандартное нормальное распределение N(0, 1). Говорят, что случайная величина χ²_n определенная как

, (1.72)

имеет распределение хи-квадрат с n степенями свободы.

Для обозначения этого распределения также обычно используется выражение χ²_n.

Ясно, что χ²_n (для любого п≥1) с вероятностью 1 принимает положительные значения. Функция плотности χ²_n в точке х(х>0) равна

, (1.73)

где Г(-) - есть гамма-функция. На практике эта плотность распределения непосредственно используется редко.

На рис. 5 изображены функции плотности распределения хи-квадрат с различным числом степеней свободы.

Рис. 5. Функции плотности распределения хи-квадрат с различным числом степеней свободы п

Математическое ожидание и дисперсия случайной величины χ²_n равны:

, (1.74)

. (1.75)

Для случайной величины χ²_n составлены разнообразные таблицы. Чаще всего они содержат значения р-квантилей случайных величин χ²_n, n=1, 2, ..., m (если вероятность выражена в процентах, их называют процентными точками и, соответственно, говорят о таблицах процентных точек). Аргумент р, 0<р<1, при этом пробегает тот или иной набор значений.

1.4.4. Распределение Стьюдента

Определение. Пусть случайные величины ξ₀, ξ₁, …, ξ_n — независимы, и каждая из них имеет стандартное нормальное распределение N(0, 1). Введем случайную величину

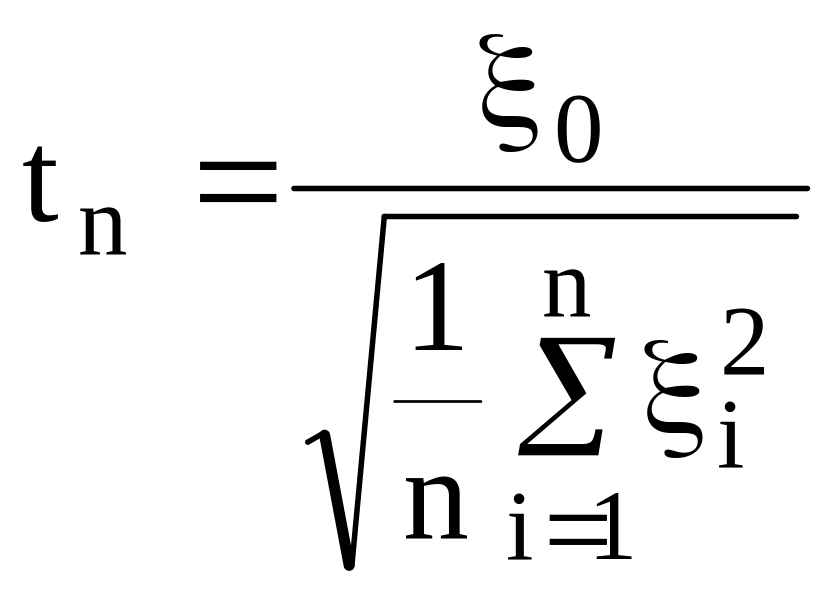. (1.76)

Ее распределение называют распределением Стьюдента.

Саму случайную величину часто называют стьюдентовской дробью, стьюдентовым отношением и т.п. Число n, n=1, 2,... называют числом степеней свободы распределения Стьюдента.

Плотность распределения Стьюдента в точке х равна

. (1.77)

Из определения видно, что плотность симметрична относительно х=0. Это обстоятельство используют при составлении таблиц.

На рис. 6 изображены функции плотности распределения Стьюдента с различным числом степеней свободы.

Рис. 6. Функции плотности распределения Стьюдента с различным числом степеней свободы n

Можно показать, что

, (1.78)

. (1.79)

В справочниках обычно приводятся таблицы процентных точек для последовательных п=1, 2,... вплоть до некоторого значения. При больших п обычно рекомендуют использовать таблицы стандартного нормального распределения, иногда с поправками.

1.4.5. Распределение Фишера (f-распределение)

Определение. Пусть η₁, …, η_m; ₁, …, _n (где m, n - натуральные числа) обозначают независимые случайные величины, каждая из которых распределена по стандартному нормальному закону N (0, 1). Говорят, что случайная величина F_m,n, определенная как

(1.80)

имеет F-распределение с параметрами m и n.

Натуральные числа m и n называют числами степеней свободы. F-распределение иногда называют еще распределением дисперсионного отношения.

Плотность F_m,n выражается довольно сложной формулой, которая редко непосредственно используется на практике, поэтому она не приводится.

На рис. 7 изображены функции плотности F-распределения с различным числом степеней свободы.

Рис. 7. Функции плотности F-распределения с различным числом степеней свободы

Математическое ожидание и дисперсия случайной величины F_m,n равны:

(1.81)

(1.82)

Семейство F-распределения зависит от двух натуральных параметров m и n, в связи с чем даже таблицы процентных точек занимают больший объем. Ради экономии места они часто публикуются в сжатом виде, поэтому при их практическом использовании приходится прибегать к дополнительны м вычислениям и интерполяции.