1.5.2. Неравенство Маркова и Чебышева

Доказательство ЗБЧ основано на неравенстве Чебышева. Неравенство Маркова в литературе называется леммой Маркова или иногда леммой Чебышева, и является частным случаем неравенства Чебышева.

Лемма Маркова. Если случайная величина Х не принимает отрицательных значений, то для любого положительного числа справедливо неравенство

. (1.103)

Доказательство.

1) Пусть Х – дискретная случайная величина, заданная рядом распределения, причем .

Все значения СВ разобьем на две группы. К первой группе отнесем значения СВ, меньшие α (пусть это будут х₁, х₂, …, х_n), а ко второй группе отнесем все остальные значения СВ, т.е. большие либо равные α (х_k+1, x_k+2, …, x_n).

Как известно, математическое ожидание дискретной случайной величины Х задается формулой:

. (1.104)

Отбросим в правой части формулы первые К слагаемых. Так как p_i>0, x_i≥0 и, кроме того, при x_i≥α, i≥k+1, будет иметь место следующее неравенство:

. (1.105)

Из выражения

(1.106)

следует, что

. (1.107)

Разделим обе части последнего неравенства на α и получим неравенство (1.103).

2) Пусть теперь Х – непрерывная случайная величина. Так как по условию Х не принимает отрицательных значений, то ее плотность вероятности f(x)=0 при всех x<0. Поэтому

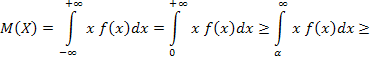
(1.108)

И опять делим на α, получаем неравенство (1.103). Лемма доказана.

Замечание. События x<α и x≥α – противоположные, поэтому, используя неравенство (1.103), получаем

. (1.109)

1.5.3. Неравенство Чебышева

Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине будет меньше данного положительного числа ε, ограничена снизу величиной , т.е.

. (1.110)

Доказательство.

Рассмотрим случайную величину ((Х-М(Х))². Она не принимает отрицательных значений, поэтому можно применить к ней лемму Маркова, а точнее, неравенство (1.109), полагая в нем α=ε²:

. (1.111)

По определению дисперсии

, (1.112)

а вероятности неравенства и - совпадают (равны), поэтому неравенство (1.5.9) принимает вид (1.110).

Замечание 1. Если случайная величина Х непрерывна, то

,

поэтому в левой части неравенства (1.103) вместо можно писать , а в левой части неравенства (1.110) вместо можно писать . Однако для дискретных случайных величин замена неправомерна.

Замечание 2. Из неравенства (1.110) переходом к противоположному событию можно получить неравенство

. (1.113)

1.5.4. Теорема Чебышева (частный случай)

Эта теорема устанавливает связь в количественной форме между средней арифметической наблюдаемых значений случайной величины Х и ее математического ожидания М(Х)=а.

Она формулируется следующим образом.

Теорема. При неограниченном увеличении числа n независимых испытаний средняя арифметическая наблюдаемых значений случайной величины сходится по вероятности к ее математическому ожиданию, т.е. для любого положительного числа ε

. (1.114)

Доказательство.

Заметим, что можно рассматривать Х₁, Х₂, …, Х_n не только как наблюдаемые в соответствующих независимых опытах значения случайной величины Х, но и как независимые случайные величины, имеющие одинаковое распределение (такое же, как у Х), в частности, одинаковое математическое ожидание а=М(Х) и дисперсию D(X). По свойствам математического ожидания и дисперсии имеем:

(1.115)

(1.116)

Применим к случайной величине х – неравенство Чебышева (1.110)

. (1.117)

Подставляя в это неравенство значения и , получим

. (1.118)

Если теперь в полученном неравенстве взять сколь угодно малое положительное ε и неограниченно увеличить n, то получим

, (1.119)

что и доказывает теорему Чебышева.

Из рассмотренной теоремы вытекает важный практический вывод. Он состоит в том, что неизвестное значение математического ожидания случайной величины можно заменить средним арифметическим значением, полученным по достаточно большому числу опытов. При этом, чем больше проведено опытов для вычисления, тем с большей вероятностью (надежностью) можно ожидать, что связанная с этой заменой ошибка не превзойдет заданную величину ε.

Кроме того, при известном значении дисперсии D(X), используя неравенство (1.110), можно решать ряд других практических задач. Например, по заданным значениям вероятности (надежности) и максимальной допустимой ошибке ε, определить число необходимых опытов n; или по заданным Р и n определить ε; или, наконец, по заданным ε и n определить границу вероятности события .