Задачи к п. 2
1. Проверить, какие из указанных функций являются функциями-оригиналами:
;
;
;
;
;
;
;
;
;
;
;
;
Пользуясь определением, найти изображения следующих функций:
2.
.
3.
.
4.
.
5.
6.
Может ли
функция
служить изображением некоторого
оригинала?
Найти изображение функций:
7.
.
8.
.
9.
.
10.
.
11.
.
12.
;
.
13.
Пусть
.
Найти изображение функции
непосредственно и с помощью теоремы
подобия.
Пользуясь теоремами линейности и подобия, найти изображения следующих функций:
14.
.
15.
.
16.
.
17.
.
18.
.
19.
.
Пользуясь теоремой о дифференцировании оригинала, найти изображение следующих функций:
20.
.
21.
.
22.
.
23.
.
24.
.
25.
.
Найти изображения следующих функций:
26.
.
27.
. 28.
.
29.
.
30.
.
31.
.
32.
.
33.
.
Найти изображения следующих функций:
34.
.
35.
.
36.
.
37.
.
38.
.
39.
.
Найти изображение функций:
40.
.
41.
.
42.
.
Найти изображения следующих функций, заданных графически:
4
3.
f(t)
1
0 1 t
f(t)
44.
1
0 1 2 t
1
4
5.
f(t)
1
0 1 2 t
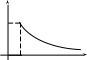
46. f(t)
1
0 a t
4
7.
f(t)
1
0 a t
48.
f(t)
a
0 a t
49.
f(t)
b-a
0 a b t
5
0.
f(t)
1
0 a 2a t
1
5
1.
5 1. f(t)
1
0 a 2a t
1
52. f(t)
2
1
0 a 2a 3a t
53.
f(t)
1
0 a 2a t
1
54.
f(t)
1
0 a 2a t
1
5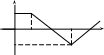
5.
f(t)
1
0 a 2a 3a 4a t
1
5
6.
f(t)
b
0 a 2a t
b
57.
Пусть функция
,
периодическая с периодом Т,
есть функция оригинал. Показать, что ее
изображение по Лапласу
дается формулой
и определено в полуплоскости
Найти изображение следующих периодических функций:
58.
f(t)
1
0 1 2 3 4 5 6 7 8 t
59. f(t)
1
0 1 2 3 4 5 t
60.
.
61.
.
62.
f(t)
1
2 3 t
.
Найти изображение следующих функций:
63.
.
64.
.
Найти оригиналы по заданному изображению:
65.
. 66.
.
67.
.
68.
.
69.
.
70.
.
71.
. 72.
.
73.
.
74.
.
75.
.
76.
.
77.
.
78.
.
79.
.
80.
.
81.
.
82.
. 83.
.
84.
.
85.
.
86.
. 87.
.
88.
.
89.
.
Решить следующие дифференциальные уравнения при заданных начальных условиях:
90.
.
91.
.
92.
.
93.
.
94.
.
95.
.
96.
.
97.
.
98.
.
99.
.
100.
.
101.
.
102.
.
103.
.
104.
.
105.
.
106.
.
107.
.
108.
.
109.
.
110.
.
111.
.
112.
.
113.
.
114.
.
115.
.
116.
.
117.
.
118.
.
119.
.
120.
.
121.
.
122. .
123.
.
124.
.
125.
.
126.
.
127.
.
128.
.
129.
.
130.
.
131.
.
132.
.
133.
.
134.
.
135.
.
136.
.
137.
.
138.
.
139.
.
140.
.
141.
.
142.
.
143.
.
144.
.
145.
.
146.
.
147.
.
148.
.
149.
.
150.
.
151.
.
152.
.
153.
.
154.
.
155.
.
C помощью формулы Дюамеля найти решения уравнений, удовлетворяющие заданным начальным условиям:
156.
.
157.
.
158.
.
159.
.
160.
.
161.
.
162.
.
163.
.
164.
.
165.
.
Решить системы уравнений:
166.
.
167.
.
168.
.
169.
.
170.
.
171.
.
172.
.
173.
.
174.
.
175.
.
176.
.
177.
.
178.
Ответы к п. 2
1. a) да; б) да; в) нет; г) да; д) да; е) нет; ж) нет; з) да;
и)
нет; к)
да; л)
да; м)
да. 2.
.
3.
.
4.
.
5.
.
6.
Нет. 7.
.
8.
.
9.
.
10.
.
11.
.
12.
а)
;
б)
.
13.
.
14.
.
15.
.
16.
.
17.
.
18.
.
19.
.
20.
.
21.
.
22.
.
23.
.
24.
.
25.
.
26.
.
27.
.
28.
.
29.
.
30.
.
31.
.
32.
.
33.
.
34.
а)
;
б)
.
35.
.
36.
.
37.
.
38.
.
39.
.
40.
.
41.
.
42.
.
43.
.
44.
.
45.
.
46.
.
47.
.
48.
.
49.
.
50.
51..
.
52.
.
53.
.
54.
.
55.
.
56.
.
58.
.
59.
.
60.
.
61.
.
62.
.
63.
.
64.
.
65.
.
66.
.
67.
.
68.
.
69.
.
70.
.
71.
.
72.
.
73.
.
74.
.
75.
.
76.
.
77.
.
78.
.
79.
.
80.
.
81.
.
82.
.
83.
.
84.
.
85.
.
86.
.
87.
88.
.
89.
.
90.
.
91.
.
92.
.
93.
.
94.
.
95.
.
96.
.
97.
.
98.
.
99.
.
100.
.
101.
.
102.
.
103.
.
104.
.
105.
.
106.
.
107.
.
108.
.
109.
.
110.
.
111.
.
112.
.
113.
.
114.
.
115.
.
116.
.
117.
.
118.
.
119.
.
120.
.
121.
.
122.
.
123.
.
124.
.
125.
.
126.
.
127.
.
128.
.
129.
.
130.
.
131.
.
132.
.
133.
.
134.
.
135.
.
136.
.
137.
.
138.
.
139.
.
140.
.
141.
.
142.
.
143.
.
144.
.
145.
.
146.
.
147.
.
148.
.
149.
.
150.
.
151.
.
152.
.
153.
.
154.
.
155.
.
156.
.
157.
.
158.
.
159.
.
160.
161.
162.
.
163
164.
.
165.
166.
.
167.
.
168.
.
169.
.
170.
.
171.
.
172.
,
.
173.
,
,
.
174.
.
175.
176.
,
.
177.
.
178.
.