4. Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.
Метод интегрирования систем линейных дифференциальных уравнений по существу не отличается от метода интегрирования одного уравнения.
Пусть требуется найти частное решение системы линейных дифференциальных уравнений с постоянными коэффициентами:
(27)
удовлетворяющее следующим начальным условиям:
(28)
В данной системе
уравнений (27)
-постоянные
коэффициенты системы уравнений ;
-заданные
функции действительного переменного
,
являющиеся функциями-оригиналами.
Функции
вместе с их производными предполагаем
непрерывными функциями-оригиналами.
Пусть
Переходя к изображениям в системе уравнений (27) и учитывая свойство дифференцирования оригинала, получим следующую систему алгебраических уравнений:
(29)
Правые части и коэффициенты системы уравнений (29) усложняются с повышением порядка уравнений исходной системы дифференциальных уравнений (27).
Найдем главный определитель системы уравнений (29)
(30)
Полагаем, что
.
Тогда, применяя формулы Крамера, получим
,
где
- вспомогательный определитель,
получающийся из главного путем замены
-го
столбца свободными членами системы
уравнений (29).
Пример 12. Найти решение системы дифференциальных уравнений
при
начальных условиях
Решение.
Если считать, что
и
,
то по теореме дифференцирования оригинала
и
(для
краткости записи мы не пишем аргументы
функций). Система операторных уравнений
примет вид
или, после преобразования,
В
результате мы получили систему
алгебраических линейных уравнений
относительно неизвестных изображений
и
Решая
эту систему, находим
и,
возвращаясь к оригиналам,
Операционный метод в равной мере применим и для решения систем уравнений с производными высших порядков.
Пример 13. Найти решение однородной системы
при начальных условиях
.
Решение. Система операторных уравнений запишется в виде
Эту систему решим при помощи определителей. Определитель системы равен
Вычислим его, опираясь на свойства определителей (сначала к первому столбцу прибавим оба остальных столбца, а затем из второй и третьей строк вычтем первую; в результате этих преобразований определитель не изменится):
=
.
Вычислим
определители
=
=
=
Теперь находим изображения искомых решений:
Для перехода к оригиналам воспользуемся формулой, согласно которой:
Применяя
теорему дифференцирования оригинала,
находим
.
Снова применяя эту же теорему, получим
Пример 14. Решить систему уравнений с заданными начальными условиями
,
.
Решение.
Пусть
;
;
.
Тогда, с учетом начальных условий,
получим
;
;
.
Переходя к изображениям запишем
Главный определитель этой системы равен
.
Вычислим вспомогательные определители
Тогда
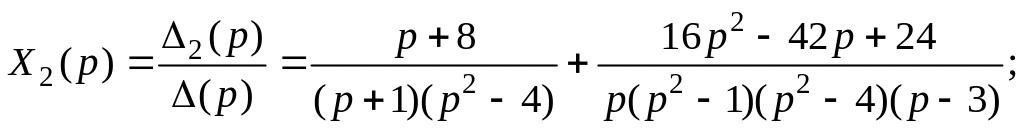
Найдем оригиналы для полученных изображений. Для этого разложим имеющиеся дроби на простейшие, используя метод неопределенных коэффициентов
Переходя к оригиналам получим решение системы:
