2.3. Применения преобразования Лапласа к решению дифференциальных уравнений и систем

1. Решение дифференциальных уравнений. Одним из важнейших применений операционного исчисления, связанных с преобразованием Лапласа, является решение линейных дифференциальных уравнений с постоянными коэффициентами. Возьмем неоднородное линейное дифференциальное уравнение второго порядка

(1)

и найдем его частное решение при начальных условиях

. (2)

Операционный метод решения такой задачи состоит в том, что мы считаем как искомую функцию , так и правую часть оригиналами и переходим от уравнения (1), связывающего оригиналы, к уравнению, связывающему их изображения и . Для этого воспользуемся теоремой о дифференцировании оригинала:

Применяя также теорему линейности, перейдем в уравнении (1) от оригиналов к изображениям:

(3)

В результате мы получили уже не дифференциальное, а алгебраическое уравнение относительно неизвестного изображения . Решая его, находим

,

откуда

. (4)

Итак, изображение искомого решения найдено. Осталось по известному изображению найти соответствующий ему оригинал ; он и будет являться искомым решением.

Операторное решение по формуле (4) имеет особенно простой вид при нулевых начальных условиях:

(5)

В этом случае

. (6)

Изложенный метод применим к решению линейных дифференциальных уравнений с постоянными коэффициентами любого порядка.

Пусть дано уравнение n-го порядка:

(7)

с начальными условиями

. (8)

Применяя преобразование Лапласа и пользуясь общей формулой (28) теоремы дифференцирования, получим

где и . Отсюда

, (9)

где а  многочлен степени не выше, чем , с коэффициентами, зависящими от начальных значений . Если, в частности, все начальные значения равны нулю: то и . (10)

Переходя в формулах (9) или (10) от изображений к оригиналам, получаем искомые решения.

При практическом решении вовсе нет нужды пользоваться готовыми формулами (9) или (10). Нужно только помнить метод их получения. Заметим еще, что если в формулах (4) или (9) считать начальные значения , ... не заданными, а произвольными постоянными, то мы получим не частное решение, а общее.

К сказанному сделаем только одно замечание. Так как правую часть уравнения (7), а также решение мы считаем оригиналами, то при их нужно считать равными нулю. Таким образом, мы получаем, вообще говоря, решение только при . Начальные значения ,... представляют при этом предельные значения соответственно , при справа. Как мы уже отмечали, при изучении физических процессов нас, как правило, интересует только течение процесса начиная с некоторого момента времени, который мы и принимаем за .

Впрочем, при решении конкретных примеров, очень часто получающееся решение оказывается справедливым при всех значениях (конечно, если и правая часть уравнения определена при всех ), хотя это и требует проверки. Перейдем к примерам.

Пример 1. Найти решение уравнения

удовлетворяющее нулевым начальным условиям .

Решение. Полагая и находя изображение правой части , составляем операторное уравнение

,

откуда .

Разложив на простейшие дроби, находим решение дифференциального уравнения: . Функция удовлетворяет уравнению при всех значениях .

При практическом решении дифференциальных уравнений операционным методом рекомендуется, конечно, пользоваться готовыми таблицами соответствия между оригиналами и изображениями. Чем эти таблицы подробнее, тем меньше придется делать дополнительных вычислений и преобразований.

Пример 2. Найти решение уравнения при начальных условиях

Решение. Найдем прежде всего изображение правой части. Так как (формула 12 табл. 1), то по теореме затухания . Учитывая, что и составим операторное уравнение:

;

отсюда .

Оригинал для первого слагаемого находим по формуле, указанной выше. Так как , то (теорема смещения в изображении).

Второе слагаемое запишем в виде

.

Тогда и окончательно

.

Можно убедиться, что если решать данное уравнение обычными методами, то это потребует гораздо более длинных выкладок.

Покажем на одном примере, как следует поступать, если начальные значения заданы не в точке .

Пример 3. Найти решение уравнения при начальных условиях .

Решение. Положим и . Так как , то уравнение и начальные условия перепишутся теперь в виде ,

(значению соответствует ). Переходя к операторному уравнению, получим

и , откуда

.

Возвращаясь к оригиналам, найдем:

.

Чтобы получить решение заданного уравнения, осталось заменить на :

.

Пример 4. Найти общее решение уравнения

.

Решение. По таблице изображений находим

.

Полагая , имеем

где числа и играют роль произвольных постоянных. Изображающее уравнение имеет вид

.

Отсюда

.

Преобразуем первое слагаемое для и найдем по таблице соответствующий ему оригинал

Для второго слагаемого имеем

Для отыскания оригинала последнего слагаемого разложим его на простейшие дроби

.

Система уравнений для определения коэффициентов разложения имеет вид

Откуда находим , , . Следовательно,

Собирая оригиналы всех слагаемых, находим решение уравнения

.

Положим , , получим

2. Применение интеграла Дюамеля. Введем сначала сокращенную запись линейного дифференциального уравнения n-го порядка. Именно, будем символом обозначать левую часть уравнения (7)

. (11)

называется линейным дифференциальным оператором n-го порядка. Числа (или функции, если речь идет об уравнениях с переменными коэффициентами) называются коэффициентами оператора.

Из самого определения следует, что

, (12)

т. е. что оператор от линейной комбинации функций равен линейной комбинации операторов от этих функций. Отсюда, кстати, и происходит название – линейный оператор.

Неоднородное уравнение сокращенно запишется в виде

(13)

Смысл применения теоремы умножения будет заключаться в том, что если нам известно решение уравнения (13) при какой-то одной правой части, то мы получим возможность с помощью свертки отыскивать решение при любой другой правой части. Особенно удобно начинать со случая, когда :

. (14)

Начальные условия будем считать нулевыми:

. (15)

Соответствующее решение обозначим через , а его изображение – через . Операторное уравнение примет вид , или

, (16)

где  характеристический многочлен. Сокращенная форма записи уравнения с помощью оператора L особенно удобна тем, что позволяет совершенно одинаково записывать как левую часть дифференциального уравнения, так и его характеристический многочлен. При этом коэффициенты оператора и многочлена совпадают.

Так как мы считаем, что решение , а следовательно, и его изображение уже известны, то из формулы (16) можно найти

. (17)

Возьмем теперь уравнение с любой правой частью при тех же нулевых начальных условиях. Его операторное уравнение где . Находя отсюда и заменяя по формуле (17), получим . Согласно формуле (36) искомое решение равно

, (18)

так как в силу начальных условий, или

(19)

Воспользовавшись коммутативностью действия свертки, можно написать еще две аналогичные формулы. Отметим, что

для получения нам не нужно знать изображение правой части уравнения.

Таким образом, зная решение для единичной правой части, мы при помощи интегрирования находим решение для любой правой части. Напомним только, что в обоих случаях начальные условия  нулевые.

Пример 5. Найти решение уравнения при нулевых начальных условиях.

Решение. Изображения функции, стоящей в правой части, мы не знаем и сначала решаем уравнение при тех же нулевых начальных условиях. Операторное уравнение

имеет решение , его оригинал равен . Поэтому по формуле (18)

.

Выразить полученный интеграл при помощи элементарных функций нельзя.

Пример 6. Решить дифференциальное уравнение

, .

Решение. Составляем вспомогательное уравнение

, .

И решаем его операционным методом:

, .

Разлагаем на простейшие дроби

.

Получаем систему уравнений, определяющую коэффициенты разложения

Подставим найденные коэффициенты в выражение и перейдем к оригиналам

,

.

Решение заданного уравнения найдем по формуле Дюамеля (5.6) с учетом того, что . Имеем

,

.

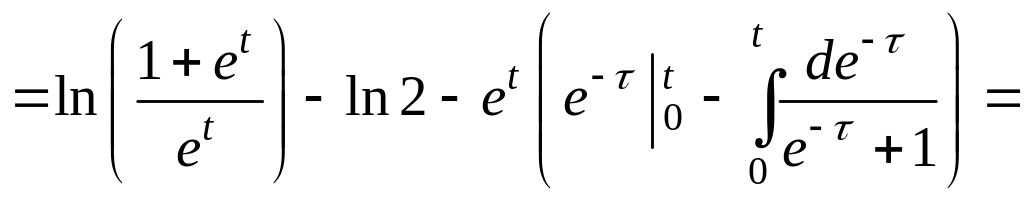
Пример 7. Записать при помощи интеграла Дюамеля решение уравнения при нулевых начальных условиях.

Решение. Начнем, как и раньше, с уравнения . Его операторное уравнение имеет решение и

. Поэтому

Пример 8. Рассмотрим включение синусоидальной ЭДС в контур, состоящий из индуктивности и сопротивления (рис.16).

L

Д

r

о момента включения ЭДС ток в цепи отсутствовал. Напряжение в цепи, вызванное включением ЭДС состоит из суммы напряжения на индуктивности и напряжения на сопротивлении .

Рис.16

Приравняв сумму напряжений в цепи электродвижущей силе получаем дифференциальное уравнение для тока в цепи

, .

Решение уравнения. Построим уравнение для изображений

.

из которого находим изображение тока в цепи

.

Для нахождения оригинала разложим дробно-рациональную функцию в правой части последнего равенства на сумму простейших дробей, используя метод неопределенных коэффициентов. Имеем,

.

Система уравнений, определяющая числа A, B, C имеет вид

Решая эту систему уравнений, получим коэффициенты разложения

, , .

Изображение тока теперь принимает вид

.

Перейдем по таблице изображений к оригиналам. Получим

.

3. Импульсные функции и их приложение к решению дифференциальных уравнений. Во многих практических задачах приходится иметь дело с кратковременными силами (например, ЭДС), имеющими характер мгновенного импульса. Эффект воздействия такой силы часто не зависит от ее вида, а зависит только от ее “площади” и не является малым, если сила достаточно велика.

Такие функции удобно представлять с помощью импульсной функции, называемой дельта – функцией Дирака.

Введем функцию , график которой изображен на рисунке 17

Рис. 17

и рассмотрим интеграл

Очевидно, что имеют место следующие равенства

, .

Если устремлять к нулю, то получится последовательность функций представляющая собой совокупность прямоугольников одинаковой площади с уменьшающимися основаниями и возрастающими высотами. Хотя рассмотренная последовательность функций и расходится, вводят условную функцию , которую считают пределом этой последовательности.

Эту условную функцию называют импульсной функцией или дельта – функцией

Для дельта – функции справедливо соотношение:

.

Физически эту функцию можно представлять как бесконечно малый промежуток с суммарным эффектом, равным I.

Дельта-функция обладает следующими “фильтрующими” свойствами для

,

, .

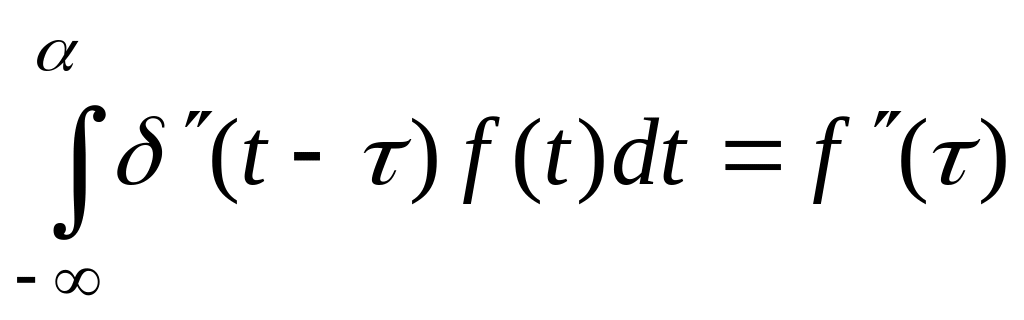Изображение дельта-функции можно получить предельным переходом при изображения функции . Очевидно

.

По теореме запаздывания получим изображение функции

.

Отсюда

(20)

Дельта - функция связана с единичной функцией Хевисайда равенством

.

На дельта функцию распространяются основные правила операционного исчисления. Например, по теореме запаздывания получим .

Рассмотрим пример, проясняющий механический смысл - функции (дельта - функции).

Пример 9. Решить уравнение

(21)

при начальных условиях . Точками обозначены производные по .

Решение. По теореме о дифференцировании оригинала имеем .

Используем формулу (20) получаем

Откуда и по таблице изображений находим решение поставленной задачи .

Продифференцируем полученное решение. Имеем при . Поскольку уравнение (21) можно рассматривать как уравнение движения материальной точки единичной массы, то видно, что -функция сообщает такой точке единичную скорость .

Пусть дано линейное неоднородное дифференциальное уравнение с постоянными коэффициентами

(22)

Определение. Элементарным решением дифференциального уравнения (22) называется функция , удовлетворяющая уравнению

при нулевых начальных значениях

Известно, что эта функция является также частным решение однородного уравнения

(23)

удовлетворяющим условиям

(25)

Элементарное решение дифференциального уравнения обладает важным свойством, позволяющим находить частное решение уравнения (22), обращающееся в нуль вместе с производными до -го порядка включительно при :

(26)

Следовательно, частное решение уравнения (22) вида

удовлетворяет условиям (25). Для получения общего решения уравнения (22) нужно к функции прибавить общее решение однородного уравнения (23).

Пример 10. Найти решение уравнения удовлетворяющее условиям

Решение. Найдем элементарное решение уравнения

Выполнив преобразования Лапласа, получим

Используя таблицу изображений, получим Для отыскания нужного решения найдем частное решение :

Искомое частное решение имеет вид

Пример 11. Рассмотрим задачу изгиба прямой балки, принимая гипотезы сопротивления материалов (гипотеза Бернулли плоских сечений).

Пусть прямая балка с осью, направленной вдоль оси , защемлена в точке и имеет свободный конец в точке . Пусть на свободный конец балки действует сосредоточенная сила , направленная в отрицательном направлении оси . Предполагая, что изгиб происходит в плоскости найти перемещение балки .

Решение. Как известно из курса сопротивления материалов, дифференциальное уравнение упругой линии балки имеет вид для

где -изгибная жесткость балки, -нагрузка. Условия защемления на концах дают

Из условия для изгибающего момента и перерезывающей силы в точке защемления

Перейдя в уравнении к изображениям, получим

,

.

По таблице изображений

Здесь мы явно ввели функцию Хевисайда, Чтобы подчеркнуть тот факт, что первый член обращается в нуль при . Таким образом, после упрощения получим