Свойства преобразования Лапласа
В
этом параграфе мы рассмотрим основные
свойства преобразования Лапласа и
составим краткую таблицу, устанавливающую
соответствие между некоторыми оригиналами
и их изображениями. Для сокращения
записи условимся, что оригиналы будут
обозначаться через f(t),
g(t)
и т. д., а их изображения соответственно
через F(p),
G(p),...,
т.е. f(t)
F(p),
g(t)
G(p).
Напомним также, что мы уже имеем формулу
соответствия (6):
и, в частности,
.
1. Теорема линейности. Для любых действительных или комплексных постоянных А и В
A f(t) + B g(t) A F(p) + B G(p), (7)
т. е. линейной комбинации оригиналов соответствует такая же линейная комбинация изображений.
В качестве применения этой теоремы найдем изображения тригонометрических и гиперболических функций. По формулам Эйлера
,
.
Полагая
в формуле (6) a
=
i
и применяя теорему линейности, получим
sin
t
,
(8)
cos
t
.
(9)
Опять пользуясь теоремой линейности, легко получим
sin(t
+)
= sin t
cos
+ cos t
sin
,
(10)
cos(t
+
)
.
(11)
Совершенно аналогично, исходя из определения гиперболических функций
sh
t
=
,
ch
t
=
найдем, что
sh
t
,
ch
t
=
.
(12)
2. Теорема подобия. Для любого постоянного > 0
f(t)
(13)
т. е. умножение аргумента оригинала на положительное число приводит к делению аргумента изображения и самого изображения F(р) на то же число .
Допустим,
что нам была бы известна формула (8)
только для частного случая
= 1, т. е. sin
t
Тогда, воспользовавшись теоремой
подобия, мы получили бы
sin
t
=
,
что в точности совпадает с формулой (8).
3. Теорема смещения в изображении (затухания). Для любого действительного или комплексного числа a
(14)
т. е. умножение оригинала, на функцию влечет за собой смещение независимой переменной р.
Теорема затухания помогает расширить таблицу соответствия между оригиналами и изображениями, позволяя по известному соотношению f(t) F(p) находить изображение функции f(t) . Например, из формул (11) и (12) получим
sin
t
,
cos
t
.
(15)
В обоих случаях мы заменили в выражении для изображения переменную p на p a.
Совершенно аналогично из формул (12) следует
sh
t
,
ch
t
.
(16)
Часто оказываются полезными формулы соответствия для произведения оригинала f(t) на sin t или cos t. Применяя теоремы затухания и линейности, легко получить формулы:
где f(t) F(p). Ясно, что формулы (15) являются частными случаями последних формул.
4. Теорема запаздывания. Для любого постоянного > 0
(17)
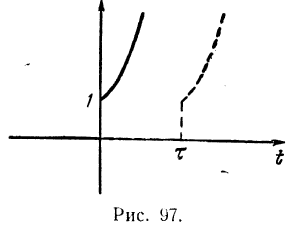
На этой теореме будет основано изображение многих функций (в частности, функций, описывающих импульсные процессы), и поэтому мы рассмотрим ее подробнее. Прежде всего выясним смысл термина запаздывание. Пусть график функции f(t) изображен на рис. 4, а. Тогда график функции f(t), изображенный на рис. 4, б, будет сдвинут относительно графика f(t) на , причем на участке (0, ) график совпадает с осью Оt, так как на этом участке t < 0 и поэтому функция f(t) равна нулю.
Рис.
4.
Таким
образом, процесс, описываемый функцией
f(t),
начинается как бы с опозданием на время
относительно процесса, описываемого
функцией f(t);
отсюда и термин запаздывание. Если,
например,
(единичная функция), то график функции
будет
иметь вид, изображенный на рис. 5. На рис.
6 сплошной линией изображен график
функции
и пунктирной
график функции f(t),
которая равна
при t
>
и 0 при t
<
. Эту функцию коротко можно записать
так:
И
сходя
из физического толкования, теорему
запаздывания можно сформулировать так:
запаздывание
оригинала на время
соответствует умножению изображения
на
Согласно этой теореме изображение
оригинала (t),
график которого изображен на рис. 5
(единичная функция, запаздывающая на
время ),
будет равно
,
а оригинала et
, сдвинутого на t
(пунктирная линия на рис. 6), есть
.
Рис. 6
Рис.
5
Применим теперь теорему запаздывания к построению изображения единичного импульса (t), действующего за промежуток времени t. График его приведен на рис. 7.
Ясно,
что этот единичный импульс можно
рассматривать как разность двух
оригиналов: единичной функции и единичной
функции, сдвинутой на t
(рис. 2 и 5). Так как изображение последней
функции есть
,
то, применяя теорему линейности, получим
(t)
.
(18)
Рис.
7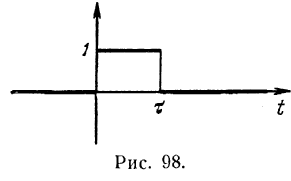
П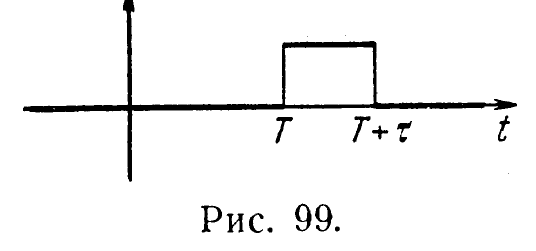
усть
теперь единичный импульс начинается
не в момент t
= 0, а в некоторый момент t
= Т
и по-прежнему действует в течение времени
t
(рис. 8).
Рис. 8
Рис.
9
Снова
применяя теорему запаздывания, получим,
что его изображение равно
Пусть,
наконец, имеется периодическая система
импульсов, изображенная на рис. 9. Ясно,
что эту систему можно рассматривать
как сумму импульсов, которые начинаются
в моменты времени
T
(
=
0,1, 2, ...) и длятся время
(
<
T
). Применяя теоремы запаздывания и
линейности, получим
Геометрическая
прогрессия сходится, потому что
если только Re
p
>
>
0. В том частном случае, когда Т
=
2,
формула упрощается: f(t)
Е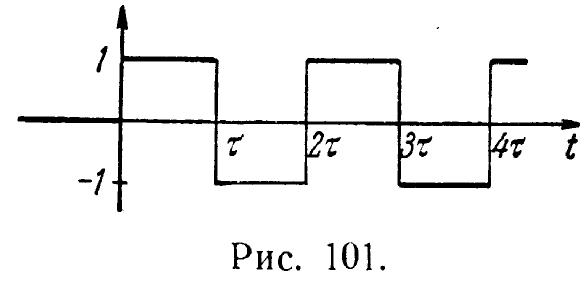
сли
в указанном частном случае первый
импульс начать не с нуля, а с момента t
= ,
то изображение опять умножится на
и будет равно
Рис.
10
Рекомендуем
самостоятельно проверить, что для
оригинала, изображенного на рис. 10, т.е.
задаваемого формулой
имеет
место соответствие f(t)
,
которое после простых преобразований
можно выразить через гиперболический
тангенс
.
Совершенно
не обязательно, чтобы все импульсы были
одинаковыми. Применяя предыдущие
формулы, легко установить, что система
двух импульсов, показанная на рис. 11,
имеет изображение
Можно также построить изображение и
периодической системы таких импульсов.
Аналогично строятся изображения
синусоидальных импульсов. Чтобы получить
импульс в виде одной полуволны синусоиды
sin
t
(рис. 12), нужно сложить два оригинала,
один из которых есть sin
t
, а другой
та же синусоида, запаздывающая на
(сплошной и пунктирный графики на рис.
13). Применяя формулу (8) и теорему
запаздывания, получим изображение такой
полуволны:
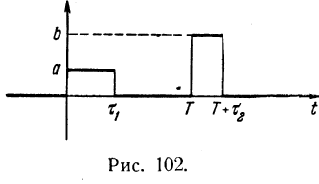
Рис. 11
Рис.
12
Такой
же импульс, начинающийся с запаздыванием
на Т,
имеет изображение
а периодическая система таких импульсов
(рис. 14, T
)
изображение
.
В
частности, если T=
, т. е. рассматривается оригинал, равный
то изображение равно
Рис.
14
Рис.
13
Теорема опережения. Если > 0, то
.
(19)
Графики функций f(t) и f( t+ ) изображены на рис. 15, причем ординаты пунктирной части графика f( t+ ) должны быть заменены нулем, так что график f( t+ ) остается как бы срезанным. Это и приводит к тому, что в формуле (19) из F(p) вычитается интеграл в конечных пределах.
Рис.
15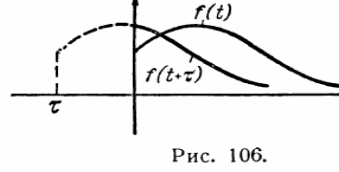
5. Оригиналы, зависящие от параметра. Для получения большого числа новых изображений оказывается удобным рассматривать оригиналы и изображения, зависящие от параметра. Пусть функция f(t,x) при каждом фиксированном значении х является оригиналом и ей соответствует изображение
.
(20)
Будем предполагать, что выполнены все условия, при соблюдении которых интеграл (20), рассматриваемый как функция параметра х, можно дифференцировать по этому параметру под знаком интеграла; тогда
.
Указанное правило дифференцирования интеграла по параметру позволяет сформулировать следующую теорему.
Теорема
о
дифференцировании по параметру.
Если
при любом значении х оригиналу f(t,х)
соответствует изображение F(р,
х),
то
.
Покажем,
как следует применять эту теорему.
Согласно формуле (6)
.
Здесь параметром является a;
дифференцируя левую и правую части по
этому параметру, получим новую формулу:
Продолжение дифференцирования приводит
к соответствиям
,
и, вообще,
(21)
Полагая a = 0, получим
(22)
Aналогично,
дифференцируя по параметру
обе части соответствий:
и
найдем
(23)
Замечание. До сих пор рассматривались те свойства преобразования Лапласа, которые применяются главным образом для расширения таблицы оригиналов и изображений. Все выведенные формулы мы сведем в краткую таблицу, приведенную на стр. 45.
Теперь
мы перейдем к наиболее важным свойствам
преобразования Лапласа, связанным с
действиями дифференцирования и
интегрирования. Предварительно сделаем
несколько замечаний. Ранее были
сформулированы три условия, при соблюдении
которых функция f(t)
является оригиналом. Дальше в качестве
оригиналов будут рассматриваться
производные функции:
,
и т.д. Поэтому, не делая в дальнейшем
никаких оговорок, будем раз и навсегда
считать, что если какая-либо производная
функция f(t)
принимается за оригинал, то для нее
выполняются все требуемые свойства.
Кроме того, если, например, в качестве
оригинала выступает первая производная,
то будем считать, что сама функция f(t)
при всех t>0
непрерывна. Если за оригинал принимается
,
то этому условию должна удовлетворять
первая производная
и т.д. В то же время, когда речь пойдет о
первообразной для функции f(t),
в частности об интеграле с переменным
верхним пределом
,
никаких дополнительных оговорок делать
не нужно. Можно показать, что если функция
f(t)
является оригиналом, то и интеграл
также является оригиналом.
Как
мы уже видели (см. рис. 2), часто случается,
что точка t=0
является точкой разрыва оригинала. Так
как нам в дальнейшем придется говорить
о значении f(0),
то условимся всегда понимать под этим
предел функции f(t)
при t
0
справа, т. е.
(24)
Аналогично, если точка t=0 является точкой разрыва для первой производной , то условимся, что
(25)
Так же поступим в случае производных высших порядков.
После сделанных оговорок перейдем к формулировке теорем.
6.
Теорема
дифференцирования оригинала. Если
,
то
(26)
т.е. дифференцирование оригинала сводится к умножению на р его изображения и вычитанию f(0).
В частности, если f(0) = 0, то
(27)
Применяя теорему повторно, получим
и, вообще,
(28)
Самый простой случай тот, когда все начальные значения функции и ее производных равны нулю:
тогда
(29)
т.е.
при нулевых начальных значениях n-кратное
дифференцирование оригинала сводится
к умножению на
его изображения.
7.
Теорема
интегрирования оригинала.
Если
и
то
(30)
т. е. интегрирование оригинала в пределах от 0 до t приводит к делению изображения на р.
Приведенные теоремы дифференцирования и интегрирования оригинала оправдывают замечание, сделанное в конце предыдущего параграфа о том, что более сложным действиям над оригиналами (в данном случае дифференцированию и интегрированию) соответствуют более простые действия над изображениями (умножение и деление на р и в первом случае вычитание постоянного числа f(0)).
Проверим
теоремы 6 и 7 на простых примерах. Так
как,
то
Исходя из соответствия
получим
что
опять-таки справедливо. Можно также
записать, что
,
и, применив теорему интегрирования,
снова получить
Вот более сложный пример: согласно формуле (15)
Поэтому, дифференцируя левую часть и умножая правую часть на р, получим соответствие
которое можно также проверить, воспользовавшись формулами (15) и теоремой линейности.
Перейдем к теоремам дифференцирования и интегрирования изображений.
8. Теорема дифференцирования изображения. Если , то
(31)
т.е. дифференцирование изображения сводится к умножению оригинала на t.
Применяя теорему несколько раз, последовательно найдем оригиналы для высших производных изображения F(р):
и,
вообще,
(32)
Пользуясь формулой (32), легко найти изображения для степенных функций tk при целых значениях k, которые мы раньше получали дифференцированием по параметру (теорема 5).
Исходя
из формулы
и применяя (32), последовательно найдем
,
т.е.
,
т.е.
и, вообще,
(формула (22)).
9. Изображение свёртки. Для того чтобы найти оригинал, соответствующий произведению изображений, познакомимся сначала с одним сравнительно простым действием над оригиналами сверткой. Начнем с определения.
Сверткой
двух функций f(t)
и
g(t)
называется
интеграл
Этот
интеграл является функцией переменной
t,
которая входит в подынтегральное
выражение и является также переменным
верхним пределом интеграла. Свертка
функций обычно обозначается символом
(33)
Выражение для свертки не зависит от порядка, в каком берутся функции f(t) и g(t) (как говорят, действие свертки коммутативно), т.е.
(34)
Приведем примеры отыскания свертки двух функций. Пусть f(t) = et и g(t) = t. Тогда
т.
е.
Теорема
умножения изображений.
Если
и
,
то свертке функций
соответствует произведение изображений
F(p)G(p). (35)
Возвращаясь
к предыдущему примеру, по теореме
умножения изображений получим
,
и действительно,
.
Свертке
должно соответствовать изображение
.
Проверка дает
Позже нам понадобится специальный случай теоремы умножения. Именно, будем искать оригинал, соответствующий произведению рF(р)G(р). Запишем это произведение в виде pF(p)G(p)= [pF(p) f(0)] G(p) + f(0)G(p). Тогда первое слагаемое в правой части есть произведение изображений, соответствующих оригиналам (теорема дифференцирования оригинала) и g(t). Применяя теоремы умножения и линейности, получим
Если записать свертку в развернутом виде, то
(36)
Последнее равенство написано на основании свойства коммутативности свертки. Формула (36) называется интегралом Дюамеля. В этой формуле можно поменять местами изображения F(p) и G(p), а следовательно, и оригиналы f(t) и g(t); тогда получатся две новые формулы, записать которые не представляет труда.
В заключение перечислим еще раз все свойства (теоремы) операционного исчисления, сохраняя прежние обозначения.
1. A f(t) + В g(t) А F(р) + В G(р) (теорема линейности).
2.
f(t)
(
> 0) (теорема подобия).
3. eat f(t) F(p a) (теорема смещения в изображении).
4. f(t ) e-p F(p) ( > 0) (теорема запаздывания).
5.
Если
то
(теорема о дифференцировании по
параметру).
6.
(теорема дифференцирования оригинала),
7.
(теорема интегрирования оригинала).
8.
(теорема дифференцирования изображения).
9.
(теорема умножения изображений),
(интеграл Дюамеля).
В таблице 1 собраны формулы соответствия, полученные в настоящем параграфе. Рядом с номером формулы в скобках стоит номер, под которым эта формула впервые встретилась в тексте.
Номер формулы |
Оригинал |
Изображение |
1(5) |
1 |
|
2(6) |
|
|
3(8) |
|
|
4(9) |
|
|
5(12) |
|
|
6(12) |
|
|
7(15) |
|
|
8(15) |
|
|
9 |
|
|
10 |
|
|
11(22) |
|
|
12(22) |
|
|
13(21) |
|
|
14(23) |
|
|
15(23) |
|
|
16 |
|
|
17 |
|
|
10. Нахождение оригинала по изображению. При нахождении оригинала по его изображению пользуются таблицей 1 и свойствами преобразования Лапласа.
Пример.
Найти
оригиналы для следующих
изображений: 1)
2)
3)
4)
5)
Решение.
При решении будем использовать таблицу
1. 1) из соотношения 12 имеем
2) из соотношения 13 имеем
3) из соотношения 3 имеем
4) из теоремы линейности и соотношения
6 получим
5) по теореме запаздывания получим
