Справедлива следующая приближенная формула

(3)

где

(4)

Это составляет содержание интегральной предельной теоремы Лапласа.

Введем функцию

(5)

называемую функцией Лапласа или интегралом вероятностей. Очевидно, Ф(х) есть первообразная для функции (х). Так как (х) > 0 в ( ), то Ф(х)  возрастающая функция в этом интервале. На основании формулы Ньютона-Лейбница из формулы (3) получаем

(6)

Это  интегральная формула Лапласа.

Как известно, интеграл не берется в элементарных функциях. Поэтому для функции (5) составлена таблица ее значений для положительных значений х, так как Ф(0) = 0 и функция Ф(х) нечетная,

Пример 5. Вероятность того, что изделие не прошло проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных изделий окажутся непроверенными от 70 до 100 изделий.

Решение. Здесь n = 400, k = 70, l = 100, р = 0,2, q = 0,8. Поэтому, в силу равенств (4) x_k = 1,25, x₁ = 2,5 и согласно формуле (6),

P₄₀₀(70, 100) = Ф(2,5)  Ф(1,25) = Ф(2,5) + Ф(1,25) =

= 0,4938 + 0,3944 = 0,8882.

3. Распределение Пуассона. Пусть производится серия п независимых испытаний (п = 1, 2, 3, ...), причем вероятность появления данного события А в этой серии Р(А) = р_n > 0 зависит от ее номера п и стремится к нулю при п  (последовательность «редких событий»). Предположим, что для каждой серии среднее значение числа появлений события А постоянно, т.е. пр_n = = const. Отсюда

Исходя из формулы Бернулли (1), для вероятности появления события А в n-й серии ровно т раз имеем выражение

Пусть т фиксировано. Тогда

(здесь использован второй замечательный предел). Поэтому

Если п велико, то в силу определения предела, вероятность Р_п(т) сколь угодно мало отличается от . Отсюда при больших п для искомой вероятности Р_n(т) имеем приближенную формулу Пуассона (для простоты знак приближенного равенства опущен)

Определение. Говорят, что случайная величина X распределена по закону Пуассона, если эта величина задана таблицей:

X	0	1	2	3	…
p					…

Здесь  фиксированное положительное число (разным значениям отвечают разные распределения Пуассона).

Найдем математическое ожидание дискретной величины X, распределенной по закону Пуассона. Согласно определению математического ожидания

Найдем далее D(X). Сначала найдем М(Х ²):

Теперь по известной формуле

Распределение Пуассона крайне важно во многих физических и биологических задачах. Оно представляет собой грубую модель частоты встречаемости катастрофических наводнений при довольно длительном периоде наблюдений. Распределение микроэлементов в образце почвы может также приближаться к пуассоновскому. Возможности приложений распределения Пуассона в естествознании иллюстрируют два следующих примера.

Пример 6. (радиоактивный распад). Рассмотрим пробу радиоактивного вещества, которое в среднем дает r импульсов радиоактивности в одну секунду. Ожидаемое число импульсов за t секунд есть rt. Этот процесс можно описать распределением Пуассона. Проба состоит из очень большого числа п радиоактивных атомов, причем каждый атом имеет крайне малую вероятность р распада в течение одной секунды. Ожидаемое число распадов за 1 секунду есть r = пр. Ожидаемое число распадов за t секунд есть rt = npt. Это является математическим ожиданием распределения Пуассона, которое дает вероятность k распадов за t секунд:

Если, например, имеется три импульса радиоактивности в 1 секунду, то вероятность возникновения 10 импульсов за 5-секундный интервал составляет

Пример 7. (подсчет клеток под микроскопом). Предположим, что n клеток определенного типа распределены случайным образом по площади предметного стекла, которое разбито квадратной решеткой на 900 (3030) равных участков. Вероятность того, что конкретная клетка лежит в данном участке решетки, есть р =1/900. Процесс размещения п клеток на предметном стекле можно рассматривать как п повторных испытаний для биномиального эксперимента, где «успех» определяется как попадание клетки в конкретный участок решетки. Если п велико, то для вычисления вероятности того, что конкретный участок решетки содержит k клеток, можно воспользоваться пуассоновским приближением биномиального распределения: = np = n/900. Значит,

Величина P(k) дает долю тех из 900 участков, в которых содержится по k клеток. Общее число участков, содержащих по k клеток, равно 900 P(k). Например, ожидается, что в среднем участков не содержат ни одной клетки.

Это дает нам метод оценки общего числа имеющихся клеток путем определения числа тех участков квадратной решетки, которые не содержат этих клеток. Если, например, мы видим, что клеток нет в 75 участках квадратной решетки, то Отсюда

Основное допущение, сделанное нами, состоит в том, что п клеток распределены по площади стекла случайно. Если это допущение справедливо, то распределение Пуассона дает весьма эффективное средство оценки числа клеток на стекле.

4. Равномерное распределение. Распределение вероятностей непрерывной случайной величины X, принимающей все свои значения из отрезка [а; b], называется равномерным, если ее плотность вероятности на этом отрезке постоянна, а вне его равна нулю, т.е.

Отсюда

(7)

Но, как известно, . Из сравнения этого равенства с (7) получаем

Итак, плотность вероятности непрерывной случайной величины X, распределенной равномерно на отрезке [а;b], имеет вид

Покажем, что Действительно,

Далее,

Пример 8. На отрезке [а;b] наугад указывают точку. Какова вероятность того, что эта точка окажется в левой половине отрезка?

Решение. Пусть X - случайная величина, равная координате выбранной точки. X распределена равномерно (в этом и состоит точный смысл слов: «наугад указывают точку»), а так как середина отрезка [а;b] имеет координату , то искомая вероятность равна

5. Закон нормального распределения. Центральная предельная теорема. Закон распределения вероятностей непрерывной случайной величины X называется нормальным, если ее дифференциальная функция f(х) определяется формулой

(8)

где параметр а совпадает с математическим ожиданием величины X: а = М(Х), параметр является средним квадра-тическим отклонением величины

График функции (8) будет иметь вид, как на рис. 18. Причем его максимальная ордината равна ). Значит, эта ордината убывает с возрастанием значения (кривая «сжимается» к оси Ох) и возрастает с убыванием значения (кривая «растягивается» в положительном направлении оси Оу), что отражено на рис. 19. Изменение значений параметра а (при неизменном значении ) не влияет на форму кривой.

Рис. 18

Нормальное распределение с параметрами а = 0 и  = 1 называют нормированным. Дифференциальная функция в случае такого распределения

Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу ( ), согласно известной теореме,

Сделаем в этом интеграле замену переменной, полагая . Тогда x = a+ и

(9)

Используя функцию (5), получаем

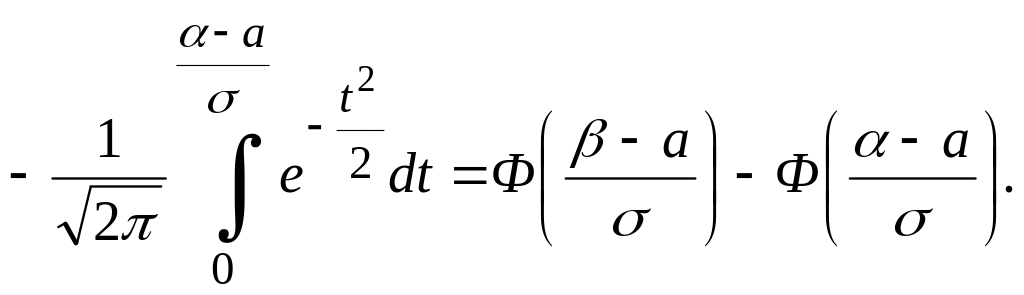
Итак,

(10)

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины X от ее математического ожидания по абсолютной величине меньше заданного положительного числа , т.е. найти . Используя формулу (10) и нечетность функции Ф(х), имеем

т.е.

(11)

Пример 9. Пусть случайная величина Х распределена по нормальному закону с параметрами а = 20 и = 10. Найти .