2.5. Решение задач кинематики

Пример 3.

Даны уравнения движения точки в плоскости :

,

( , – в сантиметрах, – в секундах).

Определить: уравнение траектории точки; для момента времени с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

Решение:

1. Для определения уравнения траектории точки исключим из заданных уравнений движения время . Поскольку входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу

:

. (102)

Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (102). Получим

,

,

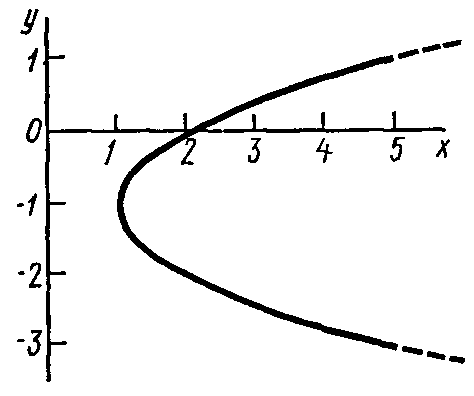следовательно,

.

О

Рис. 41

тсюда окончательно находим следующее уравнение траектории точки (параболы, рис. 41):

. (103)

2. Скорость точки найдем по ее проекциям на координатные оси:

, ,

.

Для момента времени с: , , . (104)

3. Аналогично найдем ускорение точки:

, ,

.

Для момента времени с: , , . (105)

4. Касательное ускорение найдем, дифференцируя по времени равенство:

Получим

,

откуда

. (106)

Числовые значения всех величин, входящих в правую часть (106), определены и даются в (104) и (105). Подставив в (106) эти числа, найдем сразу, что при с: .

5. Нормальное ускорение точки . Подставляя сюда найденные при с числовые значения и , получим, что .

6. Радиус кривизны траектории .

Подставляя сюда числовые значения и при с, найдем, что см.

Ответ: , , , , см.

П

Рис. 42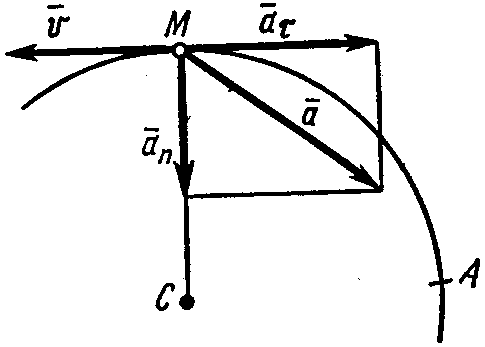

ример 4. Т очка движется по дуге окружности радиуса м по закону , ( – в метрах, – в секундах), где (рис. 42).

Определить: скорость и ускорение точки в момент времени с.

Решение:

Определяем скорость точки:

.

При с получим .

Ускорение находим по его касательной и нормальной составляющим:

, , .

При с получим , , .

Изобразим на рис. 42 векторы и , учитывая знаки и считая положительным направление от к .

Ответ: , .

П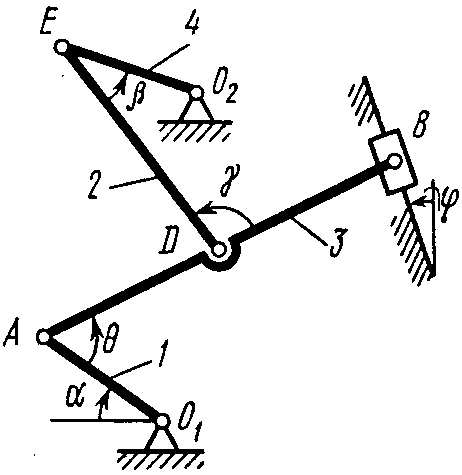 ример 5. Механизм (рис. 43) состоит из стержней 1, 2, 3, 4 и ползуна , соединенных друг с другом и с неподвижными опорами и шарнирами.

Д

Рис. К2,а.

Рис. 43

ано: , , , , , , м, м, м, с^-1, с^-2 (направления и – против хода часовой стрелки).

О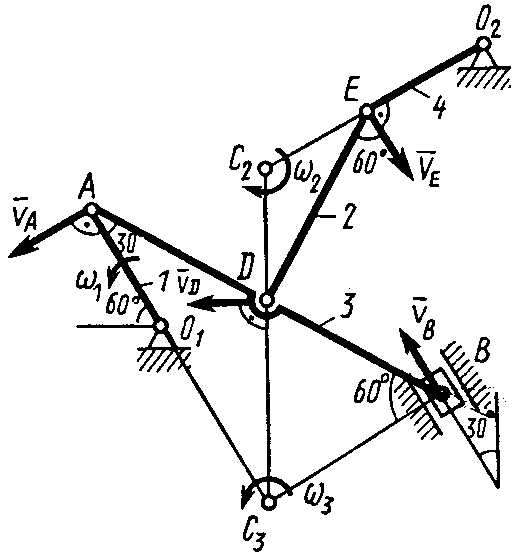 пределить: , , , , .

Решение:

1. Строим положение механизма в соответствии с заданными углами и выбранным масштабом длин (рис. 44; на этом рисунке изображаем все векторы скоростей).

2

Рис. 44

. Определяем . Точка принадлежит стержню . Чтобы найти , надо знать скорость какой-нибудь другой точки этого стержня и направление . По данным задачи, учитывая направление , можем определить . Численно:

м/с,

. (107)

Направление найдем, учтя, что точка принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная и направление , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня ) на прямую, соединяющую эти точки (прямая ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим

, м/с. (108)

3. Определяем . Точка принадлежит стержню . Следовательно, по аналогии с предыдущим, чтобы определить , надо сначала найти скорость точки , принадлежащей одновременно стержню . Для этого, зная и , строим мгновенный центр скоростей (МЦС) стержня . Это точка , лежащая на пересечении перпендикуляров к и , восставленных из точек и (к перпендикулярен стержень 1). По направлению вектора определяем направление поворота стержня вокруг МЦС . Вектор перпендикулярен отрезку , соединяющему точки и , и направлен в сторону поворота. Величину найдем из пропорции:

. (109)

Чтобы вычислить и , заметим, что – прямоугольный, так как острые углы в нем равны 30° и 60°, и что . Тогда является равносторонним и . В результате равенство (3) дает

м/с, . (110)

Так как точка принадлежит одновременно стержню , вращающемуся вокруг , то . Тогда, восставляя из точек и перпендикуляры к скоростям и , построим МЦС стержня . По направлению вектора определяем направление поворота стержня вокруг центра . Вектор направлен в сторону поворота этого стержня. Из рис. 44 видно, что , откуда . Составив теперь пропорцию, найдем, что

, м/с. (110)

4. Определяем . Так как МЦС стержня 2 известен (точка ) и м, то

с^–1. (111)

5

Рис. 45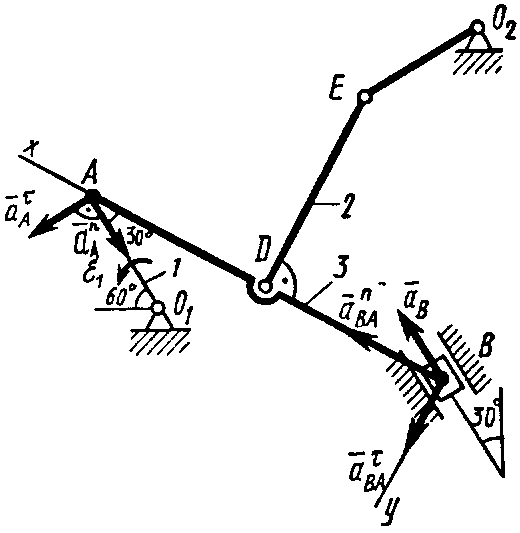

. Определяем (рис. 45, на котором изображаем все векторы ускорений). Точка принадлежит стержню . Чтобы найти , надо знать ускорение какой-нибудь другой точки стержня и траекторию точки . По данным задачи можем определить , где численно

м/с²,

м/с². (112)

Вектор направлен вдоль , а – перпендикулярно . Изображаем эти векторы на чертеже (см. рис. 45). Так как точка одновременно принадлежит ползуну, то вектор параллелен направляющим ползуна. Изображаем вектор на чертеже, полагая, что он направлен в ту же сторону, что и .

Для определения воспользуемся равенством

. (113)

Изображаем на чертеже векторы (вдоль от к ) и (в любую сторону перпендикулярно ). Численно Найдя с помощью построенного МЦС стержня 3, получим

с^–1, м/с². (114)

Таким образом, у величин, входящих в равенство (113), неизвестны только числовые значения и . Их можно найти, спроектировав обе части равенства (113) на какие-нибудь две оси.

Чтобы определить , спроектируем обе части равенства (113) на направление (ось ). Тогда получим

. (115)

Подставив в равенство (10) числовые значения всех величин из (112) и (114), найдем, что

м/с². (116)

Так как получилось , то, следовательно, вектор направлен как показано на рис. 45.

6. Определяем . Чтобы найти , сначала определим . Для этого обе части равенства (113) спроектируем на направление, перпендикулярное (ось ). Тогда получим:

. (117)

Подставив в равенство (12) числовые значения всех величин из (116) и (112), найдем, что м/с². Знак минус указывает, что направление противоположно показанному на рис. 45.

Теперь из равенства получим:

с^–2.

Ответ: м/с, м/с, с^–1, м/с², с^–2.

П

Рис. 46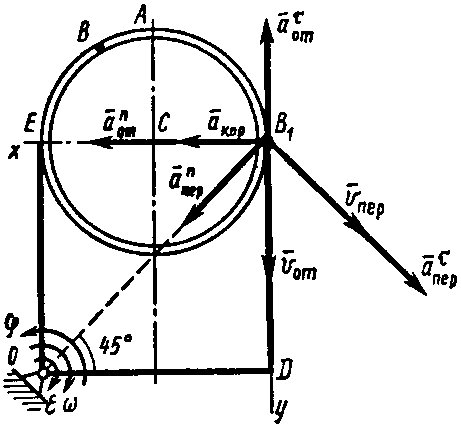

ример 6. Пластина ( , рис. 46) вращается вокруг оси, проходящей через точку перпендикулярно плоскости пластины, по закону (положительное направление отсчета угла показано на рис. 46 дуговой стрелкой). По дуге окружности радиуса движется точка по закону (положительное направление отсчета – от к ).

Дано: м, , ( – в радианах, – в метрах, – в секундах).

Определить: и в момент времени с.

Решение:

Рассмотрим движение точки как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость и абсолютное ускорение точки найдутся по формулам:

, , (118)

где, в свою очередь,

, .

Определим все, входящие в равенства (118) величины.

1. Относительное движение. Это движение происходит по закону

. (119)

Сначала установим, где будет находиться точка на дуге окружности в момент времени . Полагая в уравнении (119) с, получим

.

Тогда

.

Знак минус свидетельствует о том, что точка в момент с находится справа от точки . Изображаем ее на рис. 46 в этом положении (точка )).

Теперь находим числовые значения , и :

,

, ,

где – радиус кривизны относительной траектории, равный радиусу окружности . Для момента с, учитывая, что м, получим

м/с,

м/с²,

м/с².

Знаки показывают, что вектор направлен в сторону положительного отсчета расстояния , а вектор — в противоположную сторону; вектор , направлен к центру окружности. Изображаем все эти векторы на рис. 46.

2. Переносное движение. Это движение (вращение) происходит по закону . Найдем сначала угловую скорость и угловое ускорение переносного вращения:

,

и при с

с^–1 , с^–2. (120)

Знаки указывают, что в момент с направления и противоположны направлению положительного отсчета угла ; отметим это на рис. 46.

Для определения и находим сначала расстояние точки от оси вращения . Из рисунка видно, что м. Тогда в момент времени с, учитывая равенства (4), получим

м/с,

м/с²,

м/с². (121)

Изображаем на рис. 46 векторы и с учетом направлений и и вектор (направлен к оси вращения).

3. Кориолисово ускорение. Модуль кориолисова ускорения определяем по формуле

,

где – угол между вектором и осью вращения (вектором ). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор . Численно в момент времени с, так как в этот момент м/с, с^–1, получим

м/с². (122)

Направление найдем по правилу Н.Е. Жуковского: так как вектор лежит в плоскости, перпендикулярной оси вращения, то повернем его на 90° в направлении , т.е. по ходу часовой стрелки. Изображаем на рис. 46. (Иначе направление можно найти, учтя, что .)

Таким образом, значения всех входящих в правые части равенств (118) векторов найдены и для определения и остается только сложить эти векторы. Произведем это сложение аналитически.

4. Абсолютная скорость. Проведем координатные оси (см. рис. 46) и спроектируем почленно обе части равенства на эти оси. Получим для момента времени с:

м/с,

м/с.

После этого находим

м/с.

Учитывая, что в данном случае угол между и равен 45°, значение можно еще определить по формуле

м/с.

5. Абсолютное ускорение. По теореме о сложении ускорений

. (123)

Для определения спроектируем обе части равенства (7) на проведенные оси . Получим для момента времени с:

м/с²,

м/с²,

После этого находим

м/с².

Ответ: м/с, м/с².