4.2. Модели из жёстких блоков
Первым этапом энергетических расчётов является построение кинематически возможной модели деформируемого тела. При её выборе стремятся к тому, чтобы сложность вычислений не была чрезмерной и соответствовала уровню используемых допущений о свойствах материала и условиях его нагружения. Во многих случаях целесообразно применение кинематически возможных моделей из жёстких блоков, которые заменяют деформируемое тело в каждый момент времени механизмом с низшими парами – парами скольжения.
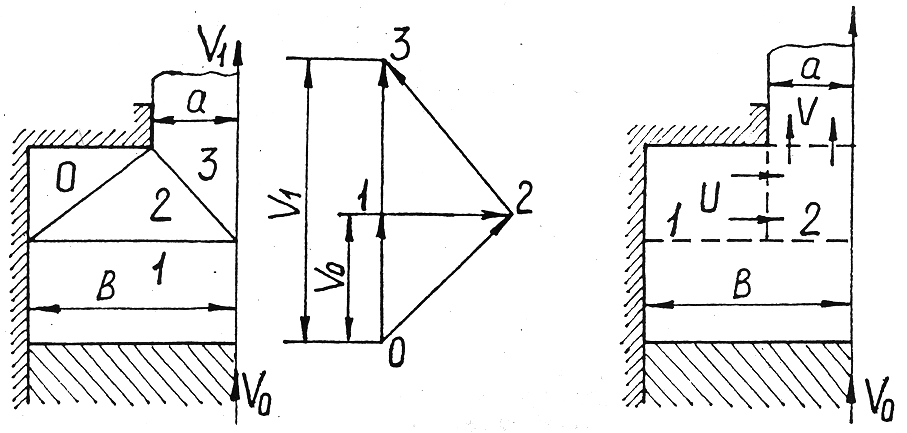
а) б)
Рис. 4.2. Рис. 4.3.
При этом все блоки являются прямыми призмами одинаковой высоты и имеют в основании, как правило, треугольник и прямоугольник (рис.4.2.,4.3.).
Построение и расчёты моделей из жестких призматических блоков, проводят, исходя из указанных ниже положений:
1. При перемещении блоков допустимо только их взаимное скольжение без обкатывания. В противном случае нарушается непрерывность нормальных составляющих скоростей на границах.
2. Система блоков должна допускать малое смещение тех элементов, которые примыкают в расчётной схеме движущемуся инструменту, если представить, что рёбра блоков притуплены.
3. Разрыв нормальных составляющих скоростей на рёбрах блоков возможен, поскольку представляет нарушение сплошности материала лишь вдоль линии.
4. В пределах каждого блока относительные деформации отсутствуют и интенсивность скоростей деформации i=0. Поверхности скольжения блоков друг по другу представляют поверхности разрыва скоростей.
5. Линии тока состоят из отрезков прямых или дуг окружности в пределах каждого блока. Изменение предела текучести упрочняемого материала происходит лишь на концах этих отрезков в результате сдвиговых деформаций на плоскостях скольжения блоков.
Равенство мощностей внешних и внутренних сил на кинематически возможных скоростях имеет вид:
(4.12)
где – мощности нагрузок деформирования Np,
мощности сил контактного трения N
мощности на разрывах скоростей N.
Находят суммированием конечного числа членов, зависящего от числа блоков и их граней:
(4.13)
(4.14)
(4.15)
здесь P – усилие деформирования;
V – скорость деформирования (скорости перемещения блоков, к которым приложены усилия P, в направлении этих сил);
B – ширина деформируемого тела, равная высоте призматических блоков;
(lc)j и (Vc)j – сторона грани блока j, скользящая по инструменту, и скорость этого скольжения;
(k)j – удельные силы трения на грани блока j со стороной (lc)j;
ljk – сторона грани блока j, скользящая по блоку K;
Vjk – скорость скольжения блока j по блоку K;
(s)jk – средний предел текучести на стыкуемых гранях
блоков j и K.
В первом приближении, обычно, в расчётах предполагают материал идеально пластичным, так что величина (s)jk постоянна.
Удельные силы трения обычно определяют в долях от величины касательного напряжения.
(4.16)
где - коэффициент, принимающий значения от нуля до единицы.