4. Приближенный энергетический
МЕТОД
4.1 Исходные уравнения
Ниже излагаются основы приближённого энергетического метода (метода верхней оценки) как метода нашедшего наиболее широкое применение в инженерной практике.
Удельная мощность пластической деформации Ny и удельная работа пластической деформации Ap в элементарном объёме тела определяется выражением:
(4.1)
Здесь
(
)0,
(ei)0
и (
)1,
(ei)1-
начальные и конечные значения
интенсивности скоростей деформаций
i
интенсивности конечных (логарифмических)
деформаций ei
в рассматриваемом объёме
(4.2)
где и έij- соответственно скорости относительных линейных и сдвиговых деформаций.
.
Мощность и работа пластической деформаций в полном объеме тела V, охваченном пластической деформацией,
;
(4.3)
М
ощность
нагрузок деформирования Р, приходящихся
на единицу поверхности, равна сумме
мощности внутренних сил Ni
и мощности сил контактного трения i,
приходящихся на единицу поверхности
контакта:
,
(4.4)
где
;
(4.5)
;
(4.6)
;
(4.7)
здесь Vg и Vc - соответственно скорость деформирования и скорость скольжения по поверхности контакта, противоположно направленные силам трения k.
Уравнение (4.4) включает дифференциальные уравнения равновесия, соотношения между напряжениями и скоростями деформаций, статические граничные условия деформации , условие пластичности.
Следовательно, если бы мы имели аналитические зависимости, отражающие действительные поля деформаций или скоростей деформаций или напряжений в виде , позволяющем получить конечное решение , задача была бы решена.
Действительными скоростями, перемещениями и напряжениями называют те , которые удовлетворяют всем уравнениям пластического равновесия и всем граничным условиям деформации. Однако в связи с большими математическими трудностями, при решении задач практически всегда используют различные аппроксимации действительных полей приближенными, разрывными, кинематически или статически допустимыми полями.
Кинематически возможными скоростями, перемещениями и напряжениями называют те, которые удовлетворяют условию сплошности (условию несжимаемости) материала и кинематическим граничным условиям.
В данной работе рассматриваются только кинематические решения.
С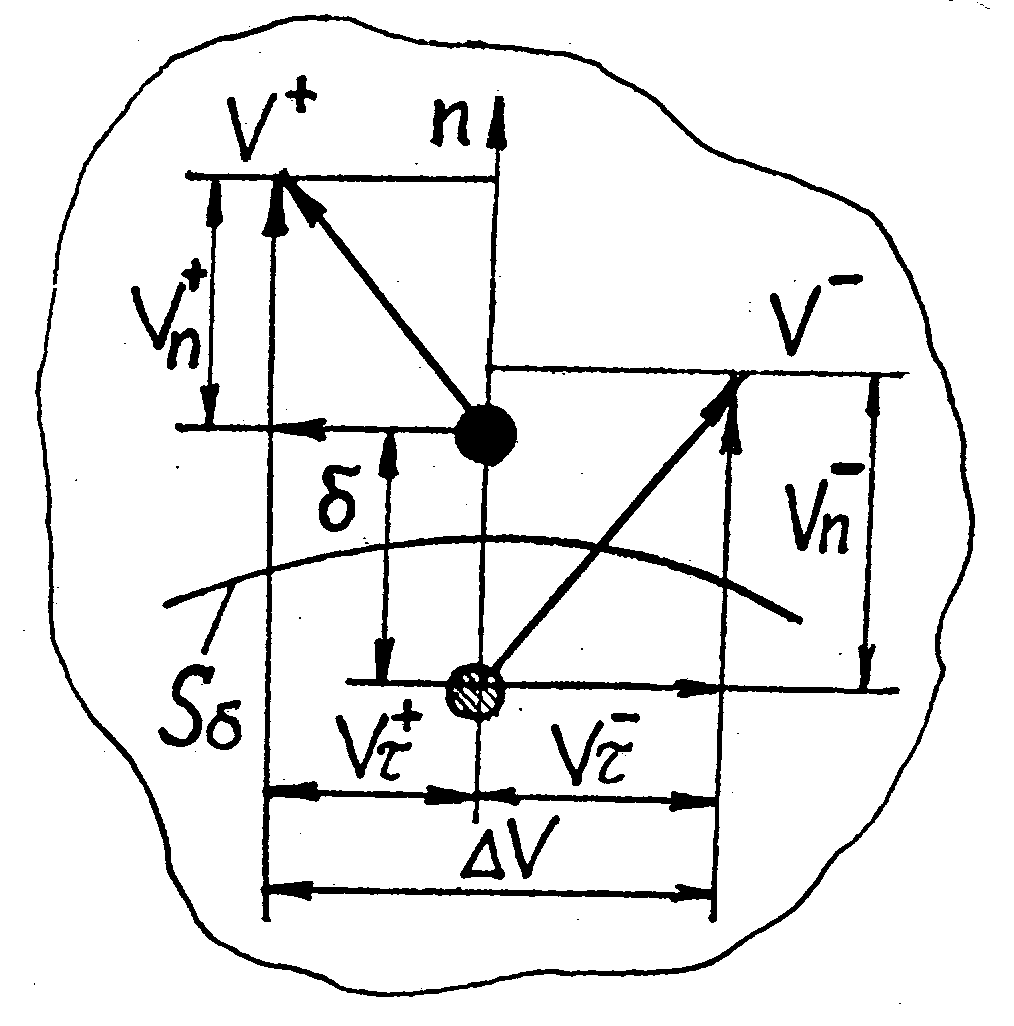
истеме
уравнений пластического равновесия
не противоречат разрывы скоростей и
перемещений в теле,
если они возникают в неограниченно
тонких слоях,
называемых
Рис. 4.1
поверхностями разрыва скоростей, и если сохраняемая сплошность материала, обеспечиваемая непрерывностью скоростей, нормальных к поверхности разрыва (рис. 4.1)
,
(4.8)
здесь
и
-
нормальные составляющие к поверхности
разрыва скоростей перемещения точек
перед этой поверхностью и за ней.
Разрыв касательных
составляющих скоростей точек перед
поверхностью разрыва
и за ней
будет
. (4.9)
С учетом выше перечисленного, можно записать равенство
(4.10)
где
и
,
(4.11)
здесь
-
мощность,
развиваемая максимальными касательными
напряжениями на всех поверхностях
разрыва
.
(i)с - средняя величина интенсивности напряжений.
Методы расчёта нагрузок, деформаций, температур в процессах пластического деформирования по равенству мощностей всех сил на кинематически возможных перемещениях называются энергетическими.
При решении задач обработки металлов давлением, связанных с большими деформациями, целесообразно применять равенство мощностей. Соответствующие расчёты разработаны наиболее полно при рассматриваемых ниже исходных допущениях:
1. Деформируемый материал жёсткопластичен. Его переход в пластическое состояние определяется величиной интенсивности напряжений i.
2. Деформируемый материал является однородным и изотропным.
3. Деформация материала является плоской.
4. Силы контактного трения не зависят от нормальных давлений.
5. Температурные напряжения и деформации, силы инерции и другие массовые силы пренебрежимо малы.
При указанных допущениях расчёты по равенству мощностей всех сил на кинематически допустимых скоростях приводит к верхним оценкам мощностей и нагрузок деформирования. Поэтому эти методы называют также методами верхних оценок.
Указанные энергетические методы расчётов позволяют также эффективно решать осесимметричные и объёмные задачи по определению нагрузок деформирования и анализа формоизменения с учётом тепловыделения и упрочнения в результате пластической деформации и с учётом контактного трения.