5.2.Проектирование кулачковых механизмов

При проведении синтеза кулачковых механизмов можно выделить три этапа:

1. Выбор закона движения толкателя (или функции положения; обычно ее записывают в виде: s = s (q), где s – перемещение толкателя, Рис. 5.3);

2. Определение минимальных размеров механизма (радиуса начальной шайбы r₀, эксцентриситета е);

3. Определение профиля кулака.

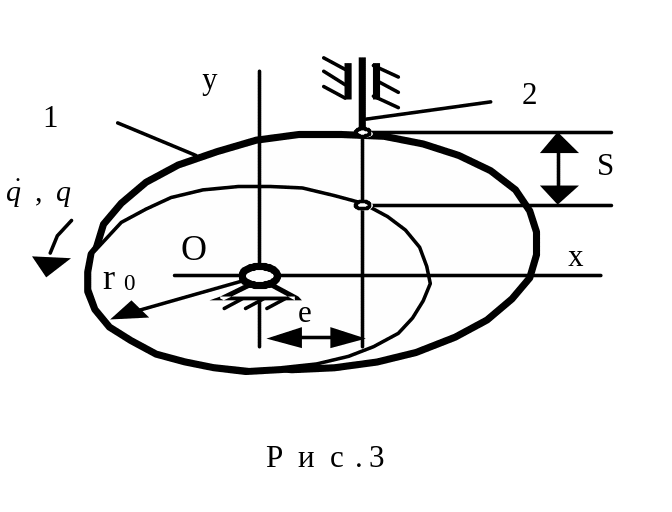
Рис. 5.33

Рассмотрим более подробно эти этапы.

I этап. В законе движения толкателя можно выделить в общем случае четыре фазы, которые представлены на циклограмме (Рис. 5.4): удаления, дальнего стояния, возвращения и ближнего стояния. На фазе удаления происходит перемещение толкателя из самого ближнего к кулаку положения. На фазе возвращения толкатель возвращается в ближнее положение. На фазах дальнего и ближнего стояния перемещения толкателя не происходит. Выбор закона движения толкателя проводится для фаз удаления и возвращения.

Четырем фазам соответствуют углы поворота кулака: q_I, q_II, q_III, q_IV. В некоторых механизмах (например, кулачковых разгружателях) фаза q_II или q_IV может оказаться равной 0. Углы q_I, q_II, q_III, q_IV обычно определяются технологическим процессом, для которого проектируется механизм, и поэтому являются заданными. Также заданным является ход толкателя – S_max.

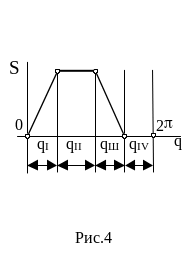
Рис. 5.34

Обычно выбирают не саму функцию s(q), а ее вторую производную – аналог ускорения s”(q). Самая простая функция s”(q) – ступенчатая (Рис. 5.5, а). Рассмотрим ее.

Введем единичную функцию :

(5.1)

Тогда s(q), q(q) и s(q) можно записать в следующем виде:

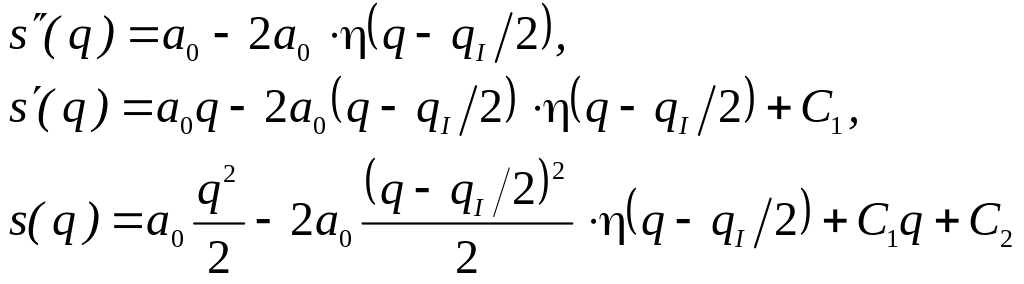(5.2)

Здесь С₁ и С₂ – постоянные интегрирования, которые найдем из начальных условий:

q = 0, s(0) = 0, s(0) = 0.

Отсюда С₁ = 0, С₂ = 0. Для отыскания амплитуды а₀ воспользуемся условием: s(q_I) = s_max, следовательно:

,

(5.3)

Зная амплитуду а₀, можно построить графики функций s(q) и s(q) (Рис. 5.5,б, в).

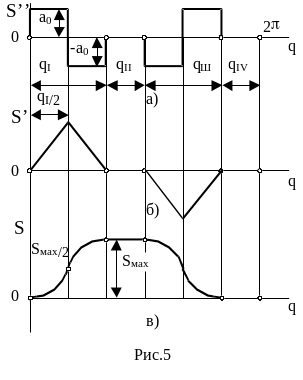
Рис. 5.35

Недостаток рассмотренного закона – скачок аналога ускорения (и, следовательно, ускорения) при q = 0, q = q_I/2 и q = q_I, что приводит к скачкообразному изменению сил инерции толкателя в этих положениях и появлению ударной нагрузки на механизм. Скачкообразное изменение ускорения называют мягким ударом. (Существует понятие и жесткого удара, при котором скачкообразно изменяется скорость толкателя, при этом ускорение стремится к бесконечности.) Для избежания ударной нагрузки используют синусоидальный закон изменения аналога ускорения (Рис. 5.6).

Рис. 5.36

Обозначив амплитуду аналога ускорения а₀, запишем s”(q), s(q) и s(q) в виде:

(5.4)

Найдем постоянные интегрирования из условий: s(0) = 0, s(0) = 0. Отсюда следует, что С₂ = 0, . Подставляя значение С₁, перепишем аналог скорости в виде:

(5.5)

Максимальный ход толкателя s = s_max будет в конце участка удаления, т.е. при q = q_I. Подставляя s(q_I) = s_max в выражение для перемещения толкателя, получим значение амплитуды a₀:

. (5.6)

Из сравнения выражений (5.6) и (5.3) видно, что безударная работа кулачкового механизма достигается за счет увеличения амплитуды а₀ в раза.

II этап. Определение минимальных размеров кулачкового механизма.

Рассмотрим пример с остроконечным поступательно движущимся толкателем (Рис. 5.7, а). В таком механизме надо выбрать минимальный радиус r₀ начальной шайбы и эксцентриситет e (расстояние от линии действия толкателя до оси вращения кулака). В этом механизме уменьшение радиуса r₀ приводит к увеличению угла давления ; при большом угле давления, как говорилось в лекции 6, возможно заклинивание механизма. Поэтому минимальные размеры механизма выбирают из условия ограничения «сверху» угла давления.

Рассмотрим графический метод. Исключая q из полученных функций s(q) и s(q), построим в координатах s0₁s две кривые, называемые характеристиками угла давления: в первой четверти – для фазы возвращения, а во второй – для фазы удаления (Рис. 5.7, б). Отметим, что аналог скорости толкателя s(q) для вращающегося кулака и поступательно движущегося толкателя измеряется в единицах длины, так же, как и перемещение толкателя s(q). Масштаб по осям s и s должен быть одинаковым!

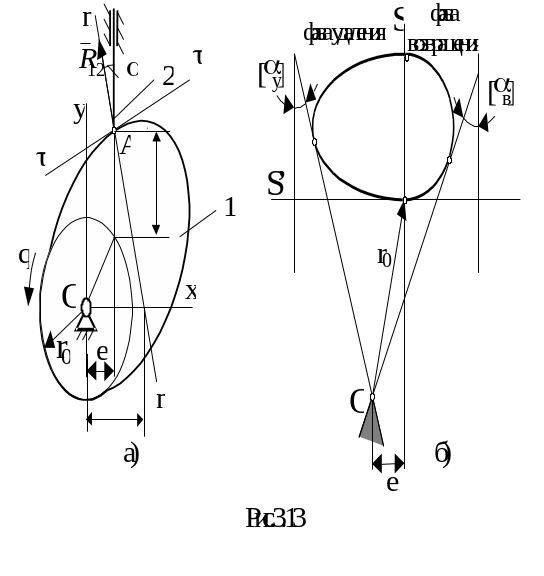
Рис. 5.37

Обозначим: [a_у], [a_в] – допустимые углы давления на фазе удаления и возвращения соответственно. Проведем касательные к характеристикам угла давления под углами к вертикальной оси: [a_у] – на фазе удаления, [a_в] – на фазе возвращения. Касательные пересекутся в некоторой точке О. Если радиус начальной шайбы выбрать равным длине отрезка ОО₁, а эксцентриситет е – равным расстоянию от точки О до вертикальной оси (см. Рис. 5.7, б), то получим минимально возможные размеры, при которых ни одно значение угла давления на фазе удаления и на фазе возвращения не превышает допустимых [a_у] и [a_в], причем в двух положениях максимальные значения углов давления равны [a_у], [a_в] (а именно в тех положениях, в которых касательные касаются характеристик угла давления). Если начало отрезка r₀ выбрать в заштрихованной области, то радиус начальной шайбы кулака увеличится, а максимальные значения угла давления уменьшатся. Поэтому, в частности, округлять значение r₀ следует в большую сторону.

Рассмотрим пример с кулачковым механизмом с плоским толкателем. В таком механизме угол давления всегда постоянный, в частности, равен 0, как на Рис. 5.8, а, поэтому внутренние условия передачи сил благоприятные, опасности заклинивания нет.

Рис. 5.38

Рассмотрим графический метод определения радиуса начальной шайбы. Можно показать, что радиус кривизны ρ_А в точке контакта А определяется следующей суммой (см. Рис. 5.8, а):

(5.7)

Для того, чтобы выполнялось условие ρ_А > 0, надо, чтобы

(5.8)

Для того, чтобы минимальный радиус кривизны кулака , надо увеличить r₀ на длину ρ_min; тогда условие (5.8) перепишется в виде:

(5.9)

Аналог ускорения толкателя s”(q) при вращающемся кулаке и поступательно движущемся толкателе измеряется в единицах длины, так же, как и перемещение толкателя s(q). Для графического определения r₀, удовлетворяющего условию (5.8), необходимо выполнить следующие построения. Из функций s(q) и s”(q) исключается q и строится кривая в координатах s”0₁s (Рис. 5.6, б), причем масштаб осей выбирается одинаковым. Под углом 45⁰ проводится касательная к отрицательной части кривой. Откладывая вниз от точки пересечения касательной с вертикальной осью отрезок, равный ρ_min, получаем точку О. Выбирая радиус r0 больше, чем длина отрезка ОО₁, мы получим выполнение условия (9) в любой точке профиля кулака.

III этап. Определение профиля кулака.

Рассмотрим пример с остроконечным толкателем. Предварительно были найдены: s(q), r₀, e. Требуется найти профиль кулака, т.е. положение точки контакта А кулака и толкателя в локальной системе координат х₁0у₁, связанной с кулаком (Рис. 5.9). Эти данные вводятся в станок с ЧПУ для изготовления кулака.

Введем векторы-столбцы:

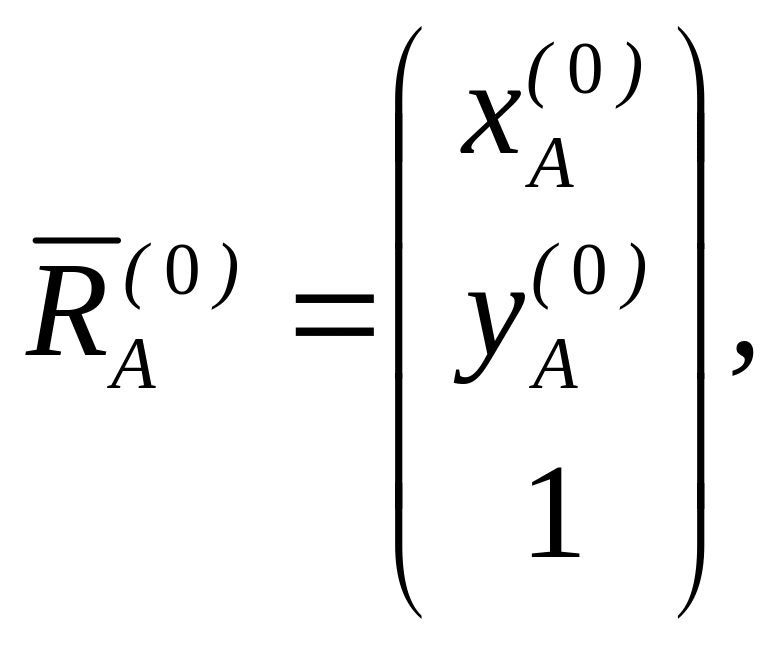
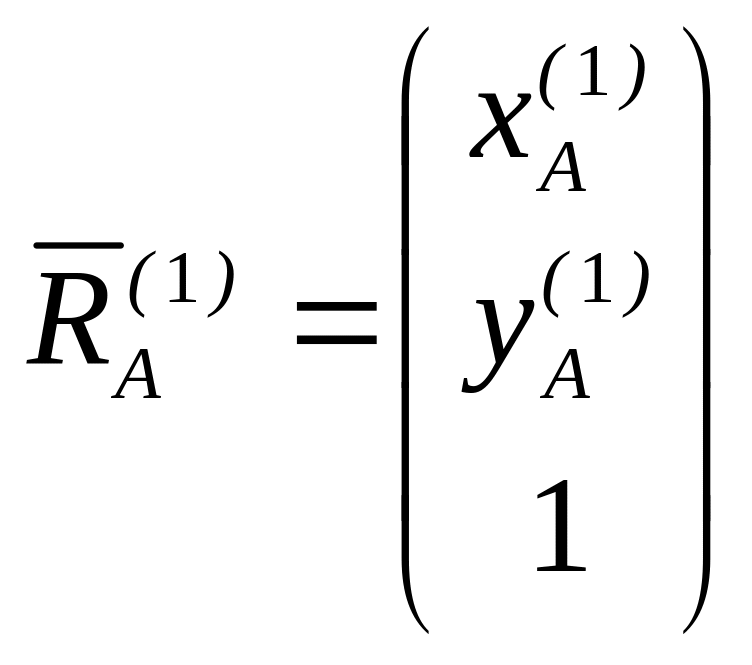(5.10)

и матрицу перехода во вращательной кинематической паре О:

(5.11)

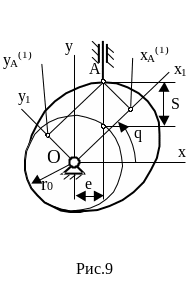
Рис. 5.39

По аналогии с пространственными механизмами запишем выражение для перехода от локальной системы координат х₁0у₁ к неподвижной системе координат х0у:

(5.12)

Отсюда найдем :

(5.13)

Матрица перехода H₀₁(q) является ортогональной; для нее справедливо:

, (5.14)

где – транспонированная матрица. С учетом (5.14) раскроем выражение (5.13):

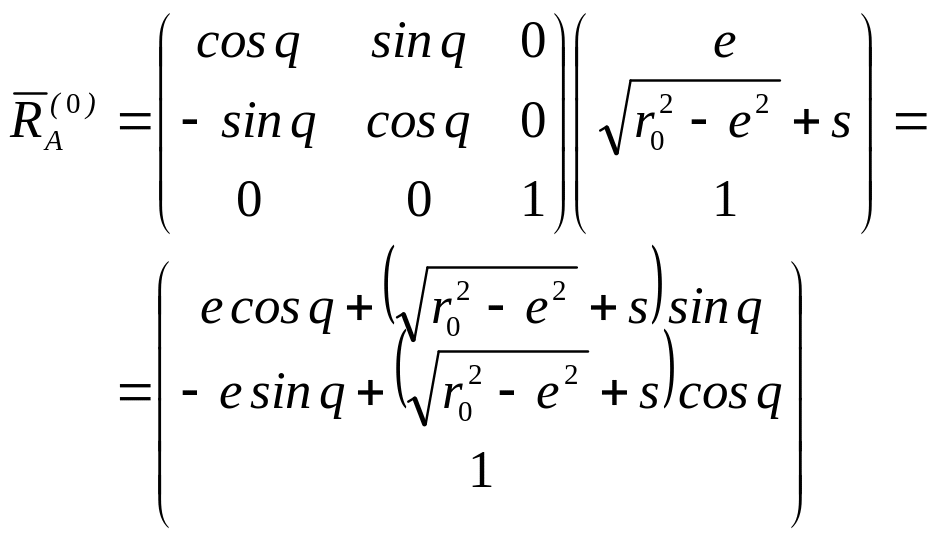(5.15)

Для замены трения скольжения на трение качения остроконечный толкатель снабжают роликом (Рис. 5.10).

Рис. 5.40

В этом случае расчетный профиль (его называют теоретическим) заменяют на эквидистанту (отстающую от теоретического профиля на радиус ролика r_p кривую), называемую рабочим профилем. Радиус ролика r_p выбирают из условия:

(5.16)

В этом случае вектор-столбец неподвижных координат точки контакта А примет следующий вид:

(5.17)

Получим выражение для профиля кулака с роликовым толкателем:

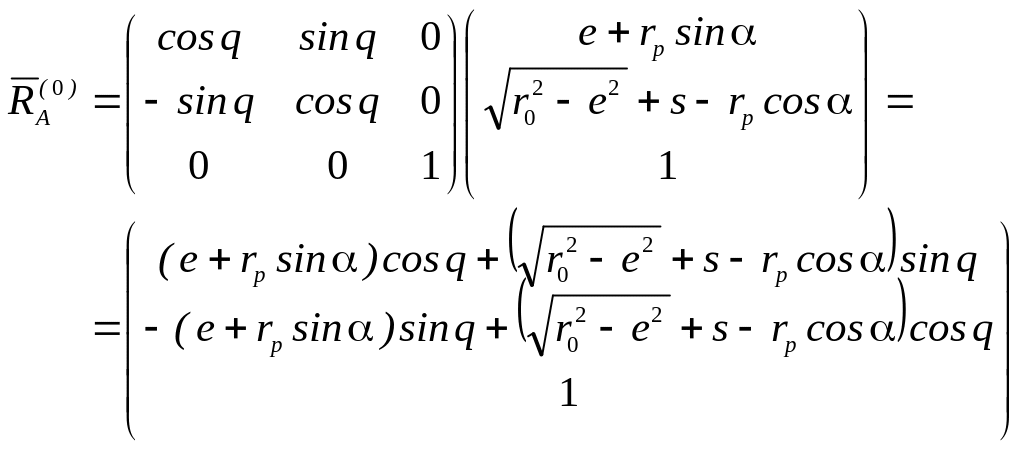(5.18)

Угол давления α в каждом положении может быть найден по следующей формуле, полученной из геометрических построений (рис. 5.7):

(5.19)

В кулачковом механизме с плоским толкателем (Рис. 5.11) изменится только вектор-столбец неподвижных координат точек контакта А:

(5.20)

Рис. 5.41

Тогда локальные координаты кулака, взаимодействующего с плоским толкателем, равны:

(5.21)

При расчете кулачкового механизма на разных этапах использовались графические и аналитические методы. В этом нет противоречия, т.к. графический метод использовался при определении минимальных размеров, где не требуется высокая точность (полученные результаты округляются); аналитические методы использовались при интегрировании закона движения и при профилировании кулака, где от точности вычислений зависит точность воспроизведения заданного закона движения.