
Основы механики. Рябцев В.А., Воропаев А.А
.pdfпри условии, что точки O1, O2, O3 не лежат на одной прямой. При решении задач можно пользоваться тремя видами
систем уравнений равновесия (7.20) - (7.22) исходя из конкретных условий задач. Выбор той или иной системы уравнений равновесия зависит в первую очередь от особенностей задачи, уровня знаний, опыта, желания и вкуса решающего.
Известно, что момент силы, отличной от нуля, относительно данной точки равен нулю, когда линия действия силы проходит через данную точку. Отсюда следует практический вывод: если при определении неизвестных сил нужно составить уравнения, в которые входят моменты этих сил, то за центр моментов О выгодно брать точку, через которую проходит линия действия одной или нескольких неизвестных сил.
7.13. Плоская система параллельных сил Если все параллельные силы лежат в плоскости х, у, то,
выбирая оси так, чтобы ось Ox была перпендикулярна силам, получим, что все Xk = 0, a Yk = Pk , где Yk – проекция силы на
ось у силы Pk . Из (7.20) остаются два уравнения
Yk 0; M0( Pk ) 0. (7.23)
Итак, для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на ось, параллельную силам, равнялась нулю и чтобы сумма моментов всех сил относительно любой точки в плоскости этих сил также равнялась нулю.
Для плоской системы параллельных сил вместо уравнений (7.21) можно записать
M01(Pk ) 0; M02( Pk ) 0, (7.24)
при условии, что отрезок O1O2 не параллелен силам.
Эта система получится из (7.21), если ось Ox направлена перпендикулярно силам.
Для плоской системы сходящихся сил можно пользоваться еще двумя видами систем уравнений вместо системы уравнений
(7.18)
60
Xk 0; M0( Pk ) 0, |
(7.25) |
|
MO1( Pk ) 0; |
MO2(Pk ) 0, |
(7.26) |
где |
|
|
MO1( R) MO1(Pk ) 0 , |
MO2(R) MO2(Pk ) 0 . |
|
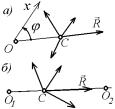
Первая из этих систем уравнений применима при условии, что ось Ox не перпендикулярна ОС (С - точка схождения сил) (рис. 7.9, а), а вторая– при условии, что прямая O1O2 не проходит через точку С схождения сил (рис. 7.9, б).
Следует помнить, что для каждой системы сил число уравнений равновесия строго определенное, хотя системы этих уравнений могут иметь различный вид. Например, для произвольной плоской системы сил имеем три уравнения равновесия, объединенных в системы одного из видов; (7.20), (7.21) или (7.22). Поэтому методами
Рис. 7.9 теоретической механики задачу о равновесии одного тела под действием системы сил, произвольно расположенных в плоскости, можно решить только в случае, когда система уравнений задачи содержит не более трех неизвестных величин. Такая задача называется статически определимой.
Для плоской системы параллельных сил имеем два уравнения равновесия в виде системы (7.23) или (7.24). Для плоской системы сходящихся сил также имеем два уравнения равновесия в виде систем (7.18). Таким образом, решить задачу о равновесии плоской системы параллельных или сходящихся сил можно только в том случае, когда число неизвестных величин в системе уравнений задачи не более двух.
Если число неизвестных величин в системе больше числа уравнений равновесия для системы, то такие задачи называются статически неопределимыми. Они решаются методами сопротивления материалов, основанными на рассмотрении
деформаций тел системы.
61
Глава 8. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ
8.1. Основные понятия и определения Движение тел чисто геометрическими методами изучалось
в кинематике. Динамика, в отличие от кинематики, изучает законы движения тел и систем тел под действием различных причин.
В статике было введено понятие о силе, как о величине, характеризующей меру механического взаимодействия материальных тел между собой. Кроме того, силы действуют на тела и материальные токи, находящиеся в силовых полях различной природы. В статике силы считались неизменными с течением времени, а движение предполагалось отсутствующим или равномерным и прямолинейным относительно инерциальной системы отсчета. В действительности, на движущееся тело одновременно с почти постоянными силами (например, силой тяжести) обычно действуют силы с изменяющимися при движении тела модулями и направлениями. Такие силы называются переменными. Переменными могут быть как заданные (активные) силы, так и реакции связей.
Из опыта следует, что переменные силы в общем случае могут зависеть от времени, положения тела и его скорости. В частности, от времени зависит сила тяги электровоза при постепенном изменении тока в обмотках тягового электродвигателя или сила, вызывающая колебания фундамента станка при обработке некоторых деталей. От положения тела зависит действующая на него гравитационная сила или сила упругости пружины. От скорости движения зависят силы сопротивления движению тела вязкой или сыпучей среды -воды, воздуха песка и т.д. Влияние именно таких сил и рассматриваются динамике.
Динамика рассматривает действие сил в данный момент времени. Поэтому все законы сложения или приведения постоянных сил, рассмотренные в статике, применимы и для переменных сил.
62
При движении тела проявляется ранее не рассматривавшееся свойство тела - инертность. Существование инертности обнаруживается при сравнении результатов действия одной и той же силы на разные тела. Опыт показывает, что если одну и ту же силу приложить к двум разным, свободным от других воздействий покоящимся телам, то в общем случае через некоторое время эти тела приобретут разные кинематические характеристикиперемещения, скорости, ускорения.
Инертность - это свойство материальных объектов двигаться с различными ускорениями под действием приложенных к ним одинаковых сил. Если, например, при действии одинаковых сил ускорение первого тела меньше, чем второго, то говорят, что первое тело более инертно, чем второе и наоборот.
Количественной мерой инертности тела является физическая величина, называемая массой тела. В механике масса m данного тела рассматривается как величина скалярная, положительная и постоянная. Единицы измерения массы рассмотрены в 8.3.
Как известно из физики масса является и мерой гравитационных свойств тела. Чтобы инертность тела и его гравитационные свойства отражала одна и та же масса, соответствующим образом была определена гравитационная постоянная
взаконе всемирного тяготения.
Вобщем случае движение тела зависит не только от массы тела и приложенных к нему сил; но и от взаимного расположения образующих его частиц, т. е. от распределения его массы по области, занятой телом.
Чтобы при изучении динамики не учитывать влияние распределения массы тела на его движение используется понятие о материальной точке.
Материальной точкой (МТ) называют тело, размерами которого при изучении его движения в данных условиях можно пренебречь. Некоторое тело можно рассматривать как МТ только в тех случаях, когда расстояния, проходимые точками тела, значительно превышают размеры этого тела. МТ, напри-
63
мер, можно считать планету при изучении ее движения вокруг Солнца или артиллерийский снаряд при определении дальности его полета в воздухе и т. п. Кроме того, поступательно движущееся тело всегда можно считать МТ с массой, равной массе тела. МТ можно считать малые частицы, на которые принято мысленно разбивать тела при определении динамических характеристик этих тел.
Ниже для краткости МТ будет называться просто точкой.
8.2.Законы динамики
Воснову динамики положены законы, обобщающие результаты опытов и наблюдений движения тел и проверенные исторической практикой. Систематически эти законы были впервые изложены И. Ньютоном в 1687 г.
Все законы Ньютона выполняются только в неподвижных системах отсчета (СО) или в системах отсчета, движущихся равномерно и прямолинейно относительно неподвижных систем отсчета. Такие системы отсчета называются инерциальными системами отсчета (ИСО). Для инерциальных систем отсчета верно утверждение: либо существует хотя бы одна ИСО
итогда таких систем существует бесконечно много, либо не существует ни одной ИСО.
Для нашей Солнечной системы ИСО с достаточной точностью можно считать систему отсчета, начало которой находится в центре Солнца, а оси направлены на так называемые неподвижные звезды. При решении большинства технических задач ИСО, с достаточной для практики точностью, можно считать систему отсчета, жестко связанную с Землей.
Первый закон динамики (закон инерции), открытый Г. Галилеем (1638 г.), гласит: МТ будет покоиться или двигаться равномерно и прямолинейно относительно ИСО (совершать инерциальное движение) до тех пор, пока она будет изолирована от внешних воздействий или воздействия на нее будут уравновешены.
Движение, совершаемое точкой относительно ИСО при отсутствии воздействия на нее сил, или воздействии на нее
64
уравновешенных систем сил, называется инерциальным движением.
Закон инерции отражает одно из основных свойств материи – пребывание в постоянном движении и устанавливает для материальных тел эквивалентность состояний покоя и инерциального движения.
Из закона инерции следует, что если к точке приложена
сила F 0, то точка покоится или движется относительно ИСО с постоянной по величине и направлению скоростью v ; ускорение точки при этом равно нулю. Если же движение точки относительно ИСО не является равномерным и прямолинейным, то на точку действует сила.
Второй закон (основной закон динамики) устанавливает
связь между массой точки m, ее ускорением aи силой F , вызывающей это ускорение и выражается формулой
F ma , |
(8.1) |
F ma. |
(8.2) |
Второй закон динамики, как и первый, выполняется только в ИСО. Из этого закона следует, что мерой инертности материальной точки является ее масса, поскольку ускорение только при равенстве их масс. Если же массы будут разные, то точка с большей массой получит меньшее ускорение, и наоборот.
Если на точку, действует одновременно несколько сил, то их действие, как известно, будет эквивалентно действию рав-
нодействующей силе R , равной векторной сумме этих сил. В этом случае уравнение основной закон динамики имеет вид
ma R или ma Fk . |
(8.3) |
Этот же результат можно получить, используя вместо аксиомы параллелограмма закон независимости действия сил, согласно которому при одновременном действии на точку нескольких, не зависящих друг от друга сил, каждая из них сообщает точке ускорение, какое она сообщила бы, действуя одна.
65
Сила тяжести. Опытом установлено, что любое тело при свободном падении на Землю (с небольшой высоты и в безвоздушном пространстве) имеет одно и то же ускорение g . Это
ускорение, сообщается телу силой тяжести G mg и называют для краткости ускорением силы тяжести, или ускорением свободного падения. Для свободного падения из (11.2) следует
G mg или m G/ g . (8.4)
Сила тяжести, как и величина g , изменяется с изменением широты и высоты над уровнем моря. Масса данного тела или материальной точки в механике считается постоянной.
Вес тела и его масса. Весом тела называется сила, с которой тело действует на его опору. Если опора тела неподвижна или движется равномерно и прямолинейно относительно ИСО,
ина тело не действуют другие силы, то вес тела равен G. В общем случае, когда опора тела вместе с телом движутся ускоренно относительно ИСО, вес тела не равен силе тяжести тела
иможет иметь любое направление и любую конечную величину.
Третий закон (закон равенства действия и противодействия) описывает механическое взаимодействие между телами. Он гласит: силы, с которыми действуют друг на друга две МТ, имеют равные модули и направлены вдоль прямой, соединяющей эти точки, в противоположные стороны.
Следует помнить что, силы взаимодействия между свободными МТ (или телами), как приложенные к разным точкам (или телам), не могут уравновесить друг друга. Например, если на гладкой горизонтальной плоскости поместить на некотором расстоянии друг от друга кусок стали и магнит, то при взаимодействии эти тела будут сближаться (а не находиться в покое).
Третий закон динамики, как описывающий взаимодействие материальных частиц, имеет большое значение в динамике системы.
8.3. Системы единиц Для измерения всех механических величин достаточно
66
ввести три основные единицы измерения.
Время определяет длительность и порядок событий. Единицей измерения времени в международной системе единиц измерения физических величин (СИ) время измеряется в секундах (с).
Единица длины служит для определения расстояний и положения точки в пространстве. В СИ время единицей измерения длины является метр (м).
В качестве третьей единицы в СИ используется единица измерения массы - килограмм массы (кг).
Единицей измерения силы в СИ является единица - 1 ньютон (Н): 1 Н - это сила, сообщающая массе в 1 кг ускорение 1 м/с2. По определению 1 Н= 1 кг*м/с2.
8.4. Основные задачи динамики для свободной и несвободной материальной точки
Для свободной МТ решаются следующие задачи динами-
ки:
1)зная закон движения точки, определить действующую на нее силу (первая задача динамики);
2)зная действующие на точку силы, определить закон
движения точки (вторая или основная задача динамики).
Решаются обе эти задачи с помощью уравнений (8.1) или
(8.3).
Втехнике очень часто приходится описывать несвободное движение точки, когда точка вынуждена двигаться по заданной поверхности или кривой. Такое движение может происходить при воздействии или регулируемых сил, или соответствующих связей. Такое движение происходит, например, при скольжении одного тела по поверхности другого тела или при полете управляемой ракеты.
Вэтих случаях, как и в статике, при решении задач используют аксиому связей, согласно которой всякую несвободную МТ можно рассматривать как свободную, отбросив связи
67
и заменив их действие реакциями этих связей N . Тогда основной закон динамики для несвободно движущейся точки примет вид
ma Fk N , |
(8.5) |
где Fk - действующие на точку активные силы.
Первая задача динамики для несвободного движения обычно состоит в определении реакции связи по закону движения точки и действующим на нее активным силам. Вторая (основная) задача динамики при несвободном движении распадается на две задачи и состоит в том, чтобы, зная действующие на точку активные силы:
1)определить закон движения точки;
2)определить реакцию связи.
8.5.Определение сил по заданному движению
(первая задача динамики)
Если ускорение движущейся точки задано, то действующая сила или реакция связи определяются по уравнениям (8.1) или (8.5). Для определения реакции должны быть заданы активные силы. Если ускорение не задано, но известен закон движения точки, то для определения силы (или реакции) надо предварительно определить ускорение по формулам кинематики.
Задача 8.1. Воздушный |
шар массы |
|
m опускается с ускорением |
a. Груз ка- |
|
кой массы m1 надо сбросить, чтобы шар |
Рис. 8.1 |
|
стал подниматься с таким же ускорением? Считать, что модуль силы сопротивления движению шара не зависит от направления его движения и равен нулю.
Решение. На падающий шар действуют сила тяжести mg и
подъемная сила F (рис. 8.1, а). Основное уравнение динамики шара имеет вид
68
ma mg F .
В проекциях на направленную вверх вертикальную ось, получим
ma mg F .
После сброса балласта (рис. 8.1, б), масса шара станет равна m m1, а подъемная сила не изменится. Тогда, учитывая, что шар при этом движется вверх, а сила сопротивления направлена вниз, получим
(m m1 )a (m m1 )g F .
Исключая из этих уравнений неизвестную силу F , найдем m1 2mg /(1 Fg / a).
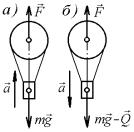
Задача 8.2. Лифт массой m (рис. 8.2) поднимается с ускорением a. Определить силу натяжения троса.
Решение. Заменив действие на лифт троса ре-
акцией Q, считаем лифт свободным. Уравнение движения лифта имеет вид ma mg Q .
Проецируя это уравнение на вертикально направленную вверх ось, получаем
Рис. 8.2
Рис. 8.3
ma mg Q.
Отсюда находим Q m( g a).
При опускании лифта с таким же ускорением сила натяжения троса будет равна
Q m( g a).
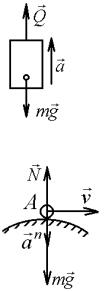
Задача 8.3. Радиус закругления в точке А моста равен R (рис. 8.3). Какую силу давления на мост в точке А оказывает автомобиль массы m, движущийся со скоростью v .
Решение. В точке А автомобиль имеет нормальное ускорение an v2 / R .
69
