Учебное пособие 800360

Колебания, совершаемые точкой по закону (11.5), называются гармоническими колебаниями.

График таких колебаний при / 2 - показан на рис. 11.2.

Проекции на ось х скорости точки

считываются отклонения точки В, называется центром колебаний.

Величина а, равная наибольшему отклонению точки М от центра колебаний О, называется амплитудой колебаний.

Величина kt называется фазой колебаний. Фаза , в отличие от координаты х, определяет не только положение точки в данный момент, но и направление ее движения. Например, из положения М при фазе, равной - точка В движется вправо, а при фазе, равной , - влево. Фазы, отличающиеся на 2 , считаются одинаковыми (на рис. 11.2 светлыми точками отмечены одинаковые фазы).

Величина определяет фазу в начале колебаний и называется начальной фазой.

140

Например, при 0 колебания происходят по закону синуса (начинаются от центра О со скоростью, направленной вправо), при / 2 - по закону косинуса (начинаются из положения х= а со скоростью v0 0 ).

Величина , обратная периоду колебаний и определяющая число колебаний, совершаемых за одну секунду, называ-

Отсюда видно, что величина k отличается от только постоянным множителем 2 .

Величины а и определяются по начальным условиям.

квадраты этих равенств, а затем, деля их левые и правые части друг на друга, получим

Свободные колебания при отсутствии сопротивления имеют следующие свойства:

1)амплитуда и начальная фаза колебаний зависят только от начальных условий;

2)круговая частота k, а следовательно, и период Т колебаний от начальных условий не зависят, (см. равенства (11.2) и

141

(11.7)) и являются постоянными характеристиками данной колебательной системы.

Отсюда следует, что для определения только периода или частоты колебаний, надо составить дифференциальное уравнение движения и привести его к виду (11.3). После этого период можно определить по (11.7) без интегрирования дифференциального уравнения колебаний системы.

11.1.1. Влияние постоянной силы на свободные колебания точки

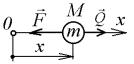
Пусть на точку М, кроме восстанавливающей силы F , направленной к центру колебаний О, действует еще постоянная по модулю и направлению сила

совпадает с уравнением (11.3). Следовательно, постоянная сила Р не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силы F, а только смещает

142

центр этих колебаний в сторону действия силы Р на величину статического отклонения 0 .

Выразим период колебаний через 0 . Из (11.10) и (11.2)

Таким образом, период колебаний пропорционален корню квадратному из статического отклонения 0 .

При колебаниях груза на вертикальной пружине (см. рис. 11.5), силой Р является сила тяжести. Тогда, формула (11.11)

Задача 11.1. Груз подвешивают к концу В вертикальной пружины АВ и отпускают без начальной скорости. Определить закон колебаний груза, если в равновесном положении растяжение пружины равно 0 - статическому удлине-

нию пружины.

Решение. Пусть груз можно считать материальной точкой, начало координат O совпадает с центром масс груза, находящегося в положении статического равновесия, а ось Ох направлена по вертикали вниз (рис. 11.5). Сила упругости F c l , где l - растяжение пружины.

Дифференциальное уравнение движения груза mx -c( 0 x) G .

По условиям задачи сила тяжести G mg F , поскольку в положении равновесия груз удерживается силой упругости пружины. Введя обозначение c/m g/ 0 k2 , получаем

x k2x 0 .

143

Период колебаний груза

T 2 /k 2 0 / g .

Следовательно, период колебаний пропорционален корню

ные условия, получим C1 0 , C2 0 . Следовательно, коле-

бания происходят с амплитудой 0 по закону x 0 coskt .

Отсюда видно, что наибольшее удлинение пружины при колебаниях груза равно 2 0 . Этот результат получается и в

том случае, когда колеблющееся тело прикреплено к какомулибо упругому телу, например к гибкой балке (см. задачу 9.6).

Рассмотренное решение подтверждает то, что постоянная сила Р не изменяет характера колебаний, происходящих под действием силы упругости F, а только смещает центр этих колебаний в сторону действия силы Р (рис. 11.5) на величину 0 . Очевидно, что при отсутствии

силы Р колебания происходили бы, около центра В.

Задача 11.2. Определить период колебаний груза массы т, подвешенного на двух пружинах с коэффициентами жесткости c1 , и c2 ,так,

как показано на рис. 11.6, а.

Решение. Каждая из пружин в статическом положении растягивается силой Р= тg. Следовательно, статические удли-

нения пружин будут равны 01 mg / c1, 02 mg / c2 . Общее удлинение пружин

0 01 02 mg(c1 c2 )/ c1c2 .

144

Эквивалентная жесткость пружины это жесткость некоторой пружины, заменяющей в колебательном процессе несколько пружин. Эквивалентная жесткость определяется по формуле

В частном случае, когда жесткости пружин одинаковы, например при c1 c2 c, получаем

c c1c2 /(c1 c2 ) 0,5c

Период колебаний системы

T 2 0 / g 2 m(c1 c2 )/ c1c2 .

Задача 11.3. Решить предыдущую задачу, считая, что груз подвешен на пружинах согласно рис. 11.6, б.

Решение. В этом случае очевидно, что статические деформации обеих пружин будут одинаковыми и равными по модулю 0 . При этом верхняя пружина будет растягиваться

силой F1 c1 0 , а нижняя сжиматься силой F2 c2 0 . Урав-

нение равновесия груза в проекциях на вертикальную ось при-

T2 0 / g 2 m /(c1 c2 ).

11.2.Свободные колебания при сопротивлении, пропорциональном скорости (затухающие колебания)

Рассмотрим влияние на свободные колебания сопротивления среды, считая, что сила сопротивления пропорциональна

первой степени скорости: R v .

145

Здесь знак минус указывает, что сила R направлена противоположно вектору скорости v колеблющегося тела. Пусть на точку при ее движении действует восстанавливающая сила

Легко проверить, что величины k и b можно сравнивать друг с другом, поскольку их размерности одинаковы (1/сек).

Уравнение (11.12) является дифференциальным уравнением свободных колебаний материальной точки при сопротивлении, пропорциональном скорости. Его решение, как и решение

уравнения (11.3), ищут в виде x ent . Подставляя это выражение в уравнение (11.12), получим характеристическое уравне-

Отсюда следует, что характеристическое уравнение имеет комплексные корни. Тогда общее решение уравнения (11.12) будет, очевидно, отличаться от решения уравнения (11.3)

только множителем e bt и примет вид

146

Входящие сюда величины а и являются постоянными интегрирования и определяются начальными условиями.

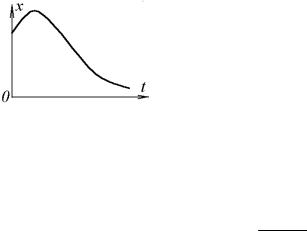
Колебания, происходящие по закону (14.17), называют затухающими, так как за счет мно-

называют периодом затухающих колебаний. За период точка совершает одно полное колебание, т. е., например, начав двигаться из положения х= 0 вправо (см. рис. 11.8), приходит в то же положение, двигаясь также вправо. Формула (11.18) с учетом равенство (11.17), принимает вид

действии сил сопротивления период колебаний несколько увеличивается. При малом сопротивлении k и b , имеют различ-

ный порядок и k >> b . Тогда величиной (b/ k )2 по сравнению с единицей можно пренебречь и считать Т1 =Т. Следовательно, малое сопротивление на период колебаний практически не влияет.

Промежуток времени между двумя последовательными отклонениями колеблющейся точки вправо (или влево) также оказывается равным Т1. Следовательно, если первое макси-

147

мальное отклонение вправо х, происходит в момент t1 то вто-

рое отклонение х2, наступит в момент t1 T1. Тогда по форму-

ле (11.17), учитывая, что kT1 2 , получим:

x1 ae -bt1 sin(k1t1 ) ,

x2 ae -b(t1 T1 ) sin(k1(t1 T1 ) ) x1 e -bT1 .

Так же для любых отклонений xn 1 и xn xn 1 xn e -bT1 .

Следовательно, максимальные отклонения материальной точки (амплитуды колебаний) убывает по закону геометрической прогрессии.

Из изложенного следует, что малое сопротивление почти не влияет на период колебаний, но вызывает постепенное их затухание - убывание амплитуды колебаний по закону геометрической прогрессии.

Пусть b> k, т. е. сопротивление по сравнению с восстанав-

ливающей силой велико. Пусть r b2 k2 . Тогда корни характеристического уравнения (14.14) будут равны n1,2 b r.

Так как r < b, то оба корня действительны и отрицательны и решение уравнения (11.12) при b>k, имеет вид

x C1e (b r )t C2e (b r )t .

Поскольку b r 0, функции e (b r )t и e (b r )t со временем монотонно убывают, асимптотически стремясь к нулю. Движение точки в этом случае не будет колебательным. Точка M под действием восстанавливающей силы будет асимптотически приближаться к положению равновесия, при котором х=

148

0. График такого движения с начальными условиями при t = 0 x x0 , vx 0 показан на рис. 11.9.

11.3. Вынужденные колебания. Резонанс.

Пусть кроме восстанавливающей силы F на точку действует и периодически изменяющаяся со временем сила Q, проекция которой на ось Ох (рис. 11.10) равна

Qx Q0 sin pt . (11.19)

Эта сила называется возмущающей (возбуждающей) силой, а колебания при действии такой силы, называются вынужденными. Величина р в (11.19) называется частотой возмущающей силы.

Возмущающей силой может быть и сила, изменяющаяся со временем по произвольному периодическому закону.

Рис. 11.10

Рассмотрим случай, когда Q изменяется

по закону (11.19). Такая возмущающая сила называется гармонической. Подобная сила возникает при вращении тела, центр тяжести которого смещен относительно оси вращения (см. задачу 11.4).

11.3.1. Вынужденные колебания при отсутствии сил сопротивления

Пусть на точку кроме восстанавливающей силы F (см. рис. 11.10), действует только возмущающая сила Q. Дифференциальное уравнение движения в этом случае имеет вид

mx -cx Q0 sin pt .

149