Учебное пособие 800360

9.6. Теорема об изменении кинетической энергии точки

Пусть точка массы m, перемещается под действием приложенных к ней сил из точки M0 , где она имела скорость v0 , в

точку M1 , где ее скорость равна v1.

Для получения зависимости кинетической энергии точки от работы силы используем соотношение mv Fk , выра-

жающее основной закон динамики. Проецируя это равенство на касательную M к траектории точки М, направленную по скорости точки, получим

ma Fk .

Модуль касательного ускорения представим в виде

Тогда mv dvdr Fk .

Умножив это равенство на dr , и, внеся m под знак дифференциала (поскольку масса постоянна), получим выражение теоремы об изменении кинетической энергии в дифференциальной форме

0,5d mv2 dAk ,

где dAk Fk dr - элементарная работа силы Fk .

Проинтегрировав обе части этого равенства в пределах, соответствующих значениям переменных в точках M0 и M1 ,

получим

Это соотношение выражает теорему об изменении кинетической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно сумме работ всех действующих на точку сил на том же перемещении.

100

Следует помнить, что соотношение (9.18) верно только в том случае, когда и скорость точки и ее траектория определены относительно одной и той же инерциальной системы.

9.6.1. Несвободное движение При несвободном движении точки, как следует из (9.5), в

правую часть равенства (9.18) войдет работа заданных (актив-

ных) сил Fk и работа реакции связи N . Пусть точка движется по неподвижной поверхности или кривой. При отсутствии трения реакция N направлена по нормали к траектории точки и N 0. Согласно (9.11), работа реакции неподвижной глад-

кой поверхности (или кривой) при любом перемещении точки

Следовательно, при перемещении по неподвижной гладкой поверхности (или кривой) изменение кинетической энергии точки равно сумме работ приложенных к точке активных сил на этом перемещении.

Если поверхность или кривая не является гладкой (имеется трение), то к работе активных сил прибавится работа силы трения. Если же поверхность или кривая движется, то абсолютное перемещение точки М может не быть перпендикуляр-

но N . Тогда работа реакции N не будет равна нулю (например, работа реакции пола лифта, поднимающего тело).

9.7. Решение задач Приступая к решению, следует прежде всего установить,

можно ли для решения данной задачи непосредственно воспользоваться какой - либо из доказанных выше теорем. Важно помнить, что с помощью теоремы об изменении импульса точки легко решаются задачи, в которых:

а) действующие силы постоянны, или зависят только от времени;

101

б) в число данных и искомых величин входят: действующие силы, время движения, начальная и конечная скорости точки (т. е. величины F,t,v0 ,v1).

С помощью теоремы об изменении кинетической энергии точки легче решаются задачи, в которых:

а) действующие силы постоянны, или зависят только от перемещения;

б) в число данных и искомых величин входят: действующие силы, перемещение точки, скорости в начале и в конце перемещения (т. е. величины F,s,v0 ,v1 ).

Если среди действующих сил есть сила, зависящая от скорости движения, то решить основную задачу динамики с помощью какойлибо из общих теорем нельзя, поскольку нельзя заранее вычислить работу или импульс такой силы. В этом случае надо интегрировать дифференциальные уравнения движения.

Применяя обе теоремы одновременно, можно решить некоторые смешанные задачи, в которых данными (или искомыми) являются и время движения, и перемещение точки.

Рекомендуется следующий порядок решения:

1.По данным задачи определить, какой из теорем можно воспользоваться для ее решения.

2.Изобразить на чертеже движущуюся точку в произвольном положении и показать все действующие на нее активные силы и реакции связей (если движение подчинено связям).

3.Вычислить по соответствующим формулам импульсы или работу всех сил за время движения.

4.Пользуясь равенствами (9.6) или (9.18), составить соответствующие уравнения и определить из них искомые величины. При всех вычислениях следует обращать особое внимание на то, чтобы все величины определялись в одной и той же системе единиц.

Доказанные теоремы позволяют также по изменению импульса или кинетической энергии точки определить импульс

102

или работу действующих на точку сил (первая задача динамики).

Задача 9.1. Тело массой m = 0,1 кг движется равномерно со скоростью v= 2 м/с по окружности. Определить импульс и работу действующей на тело силы за время, в течение которого тело

Рис. 9.10

пройдет четверть окружности. Решение. По теореме об изме-

нении импульса p mv1

mv0 . Изобразив векторную разность этих импульсов, из прямоугольного треугольника находим p mv12 v02 .

Поскольку по условиям задачи v1 v0 v ,

p mv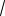2 0,029 кг*м/с.

Согласно (9.18), AM0M1 0,5m v12 v02 0 .

Задача 9.2. Телу массы m, лежащему на горизонтальной плоскости, сообщают толчком начальную скорость v0 . После-

дующее движение тела тормозится постоянной силой F . Определить, через какое время тело остановится, и какой путь оно пройдет до остановки?

Решение. Из условия задачи следует, что для определения времени движения можно воспользоваться первой, а для определения пройденного пути - второй из доказанных теорем.

Изображаем тело в произвольном положении М (М0 и М1, - его начальное и конечное положения). На

тело действуют: сила тяжести G ,

реакция поверхности N и тормо103

зящая сила F (рис.9.11). Направляя ось Ох в сторону движения, составляем уравнение (9.6)

mv1x mv0x pix . (а)

В данном случае v1x 0 (v1 - скорость в момент останов-

ки), a v0x v0 . Из сил проекцию на ось Ох дает только сила F .

Так как она постоянна, то px Fxt1 Ft где t1время тормо-

жения. Подставляя все эти данные в уравнение (а), получаем

Работы сил G и N равны нулю, так как они перпендикулярны

Из формул (б) и (в) видно, что при данной силе F время торможения растет пропорционально начальной скорости v0 , а

тормозной путь – пропорционально квадрату начальной скорости.

Если тормозящей силой является сила трения и коэффици-

определения тормозного пути s1 этих данных было бы недостаточно.

104

Решение. Так как в условия задачи входят: перемещение груза, определяемое углом поворота нити, и скорости v0 и v1

воспользуемся для решения теоремой об изменении кинетической энергии

0,5(mv12 mv02 ) AM0M1 .

На груз действуют сила тяжести G и реакция нити N . Ра-

Это - известная формула Галилея. Очевидно, такой же результат получится для скорости v свободно падающего груза с высоты h .

В рассматриваемой задаче h lcos lcos 0 и v1 2gl cos cos 0 .

Задача 9.5. Пружина клапана (рис. 9.14) имеет в свободном состоянии длину l0 6 см.

При полностью открытом клапане длина пружины l 4 см, а высота подъема клапана s = 0,6 см. Жесткость пружины с = 1 H/см, масса клапана m = 0,4 кг. Пренебрегая действием силы тяжести и сил сопротивления, определить скорость

Рис. 9.14 клапана в момент его закрытия.

Решение. Действующая на клапан сила упругости F зависит от расстояния; кроме того, задано перемещение s клапана. Поэтому для решения задачи удобно использовать уравнение

(12.18)

0,5(mv12 mv02 ) AM0M1 .

По условиям задачи работу совершает только сила упругости пружины. Тогда, согласно (9.15),

AM0M1 0,5c lнач 2 lкон 2 . 106

В данном случае

lнач l0 l 2 см, lкон l0 l s 1,4 см.

Подставляя v0 0 и все эти значения в (9.18), получим

v1 c lнач 2 lкон 2 0,22 м/с. m

Задача 9.6. Под действием груза, лежащего на середине упругой балки (рис. 12.15), балка прогибается на величину ст

(статический прогиб балки). Пренебрегая силой тяжести балки, определить ее максимальный прогиб m , если груз упадет

на балку с высоты Н из состояния покоя.

Решение. Как и в предыдущей задаче, воспользуемся для решения уравнением (9.18). В данном случае начальная скорость груза v0 и конечная его скоростьv1 (в момент макси-

мального прогиба балки) равны нулю и формула (9.18) принимает вид

Решая это квадратное уравнение, и учитывая, что по условиям задачи должно быть m 0, находим

m ст ст2 2H ст .

Важно отметить, что при H= 0 получается m 2 ст . Сле-

довательно, если груз положить на середину горизонтальной балки, то ее максимальный прогиб под действием отпущенного груза будет равен удвоенному статическому. В дальнейшем балка с грузом начнет совершать колебания около положения равновесия. Под влиянием сопротивлений эти колебания затухнут и система окажется равновесии в положении, когда прогиб бал-

ки будет равен ст .

сти Земли на заданную высоту Н. Cила притяжения изменяется обратно пропорционально квадрату расстояния от центра Земли (рис. 9.16). Сопротивлением воздуха пренебречь.

Решение. Для решения задачи воспользуемся теоремой об изменении кинетической энергии, считая тело материальной точкой. Тогда

Поместим начало координат в центре О Земли (центр притяжения) и направим ось Ох в сторону движения. Изобразим в произвольном положении точку М и действующую на нее силу

F . По условиям задачи F km / x2 .

Коэффициент пропорциональности k находится из условия, что на поверхности Земли, т. е. при x= R (R - радиус Земли), сила притяжения равна mg (g - ускорение силы тяжести на

земной поверхности). Отсюда mg kmR 2 и k gR2 . 108

Этот же результат можно получить сразу по формуле (9.17), если учесть, что в данном случае r0 R, а r1 R H .

Поскольку в наивысшем положении M1 , скорость точки v1 0, подставляя в (а) величины работы и k, получим

v0 2gRH /( R H ).

Рассмотрим частные случаи.

а) Пусть H очень мало в сравнении с R. Тогда H/R - величина, близкая к нулю. Деля числитель и знаменатель на R, по-

лучим v0 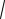2gH /(1 H / R) 2gH .

Следовательно, для малых Н получается формула Галилея. б) Определим начальную скорость, при которой брошенное тело уйдет в бесконечность. Деля числитель и знаменатель

Следовательно, тело, брошенное с поверхности Земли со скоростью 11,2 км/сек, навсегда покинет поле земного тяготения.

Можно показать, что при начальных скоростях, лежащих приблизительно в пределах 8 км/с v0 11 км/с, тело, бро-

шенное по направлению касательной к земной поверхности, не упадет обратно на Землю, а превратится в земной спутник. При начальных скоростях, меньших 8 км/с, или при негоризонтальном бросании тело, описав эллиптическую траекторию,

109