Учебное пособие 800360

ветствующий рулевой винт. У двухвинтового вертолета несущие винты делают вращающимися в разные стороны.

Появление реактивного момента можно использовать для экспериментального определения вращающего момента авиационного двигателя, так как эти моменты равны друг другу по модулю, а реактивный момент можно измерить, установив двигатель с вращающимся винтом на соответствующих весах.

15.4. Решение задач Теоремой моментов пользуются для изучения вращатель-

ного движения тел или для изучения движения систем, включающих вращающиеся и поступательно движущиеся тела.

Закон сохранения момента импульса позволяет по величине скорости перемещения одной части системы определить изменение угловой скорости, или угол поворота другой ее части. При этом из рассмотрения исключаются все, как правило, неизвестные внутренние силы, а также внешние силы, не создающие моменты относительно оси вращения, то есть пересекающие ось вращения или параллельные этой оси.

Задача 15.1. Два диска насажены на общий вал (рис. 15.3). В некоторый момент времени вал слегка закручивают и предоставляют самому себе. Пренебрегая массой вала, определить зависимость между угловыми скоростями и углами поворотов дисков при их крутильных колебаниях, если моменты инерции дисков J1 , и J2, относительно оси z известны.

Решение. Чтобы исключить неизвестные упругие силы, вызывающие колебания дисков, рассмотрим оба диска и вал как одну систему.

220

ментов импульсов дисков относительно оси z должна быть равна нулю: Kz J1 1 J2 2 0 . При получении этого выражения использовано очевидное условие: момент импульса системы относительно оси z равен сумме моментов импульсов каждого из дисков относительно той же оси. Отсюда

1 J2 2 / J1 и 1 J2 2 / J1,

где 1 и 2 - углы закручивания дисков, отсчитываемые от начального положения.

Соотношение между углами получено интегрированием соотношения между скоростями.

Таким образом, колебания будут происходить с противоположно направленными скоростями, а угловые амплитуды колебаний будут обратно пропорциональны моментам инерций дисков. Неподвижное сечение вала будет ближе к диску с большим моментом инерции.

Задача 15.2. В регуляторе АВ, имеющем вертикальную ось вращения Oz (величина Jz регулятора известна), помещены два симметрично расположенных груза массы m каждый, прикрепленных к пружинам (рис. 15.4). В момент t0 = 0 угловая скорость регулятора имеет величину 0 , а каждый из

грузов начинает совершать одинаковые затухающие колебания около центра С, удаленного от оси z на расстояние l. Пренебрегая трением в

Рис. 15.4 опорах оси и считая грузы материальными точками,

определить закон изменения угловой скорости регулятора в зависимости от положений грузов.

Решение. Чтобы исключить неизвестные упругие силы пружин, рассмотрим регулятор и грузы как одну систему. То-

221

гда силы упругости пружин станут внутренними силами. Эти

вольный момент времени t величина Kz ( Jz 2m(l x)2 ) . Поскольку Kz0 Kz ,

Следовательно, когда x > 0, 0 , а когда x < 0, 0 .

Поэтому угловая скорость колеблется около среднего значения 0 . С течением времени при затухании колебаний гру-

зов х стремится к нулю и стремится к 0 .

Задача 15.3. По ободу круглой горизонтальной платформы массы M радиуса R проложены рельсы (рис. 15.5). Платформа вместе со стоящим на рельсах заводным вагончиком массы m вращается вокруг вертикальной оси Oz с угловой скоростью0 . В некоторый момент времени

вагончик начинает двигаться по рельсам относительно платформы со скоростью u в сторону вращения платформы. Как изменится при этом угловая скорость платформы?

Решение. Чтобы исключить неизвестные силы трения между коле- Рис. 15.5 сами вагончика и платформой, считаем платформу и вагончик одной

системой. Моменты действующих на эту систему внешних сил относительно оси z равны нулю. Следовательно, Kz = const. Пусть платформа - однородный круглый диск, а вагончик - материальная точка. Тогда их моменты инерции относительно

222

оси z будут равны 0,5MR2 и mR2 . Момент импульса системы в начале движения вагончика Kz0 (0,5MR2 mR2 ) 0 .

Абсолютная скорость движущегося вагончика, равна v u R , где - мгновенная угловая скорость платформы. Момент импульса вагончика относительно оси z равен

mvR m(uR R2 ). Момент импульса системы

Kz1 (0,5MR2 m(uR R2 ).

Так как Kz = соnst, то Kz1 Kz0 . Следовательно

Как видно, при движении вагончика в сторону вращения платформы, угловая скорость платформы, уменьшается. Если вагончик будет двигаться в противоположную сторону, то угловая скорость платформы увеличится.

Задача 15.4. На барабан массы M и радиуса r (рис. 15.6) намотана нить с грузом А массы m на конце. Без учета массы нити и трения в опорах оси, определить угловое ускорение барабана при вертикальном движении груза, если радиус инерции барабана относительно его оси равен

.

Груз, движущийся поступательно, можно считать материальной точкой. Его скорость v r . Барабан вращается вокруг неподвижной оси. Следовательно,

223

K2 mvr m r2, K1 J0 M 2 .

Момент импульса системы Ko (M 2 mr2 ) .

Подставляя Ko в (а), получим

(M 2 mr2 ) mgr .

Отсюда определяется мгновенное угловое ускорение бара-

бана mgr /(M 2 mr2 ).

Это ускорение постоянно, что и следовало ожидать при постоянных движущих силах и силах сопротивления.

Аналогичный результат получается и при использовании основного закона динамики.

15.5.Задачи для самостоятельного решения

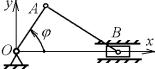
15.5.1.Механизм эллипсографа со-

стоит из ползунов А и В массой m каждый, кривошипа ОС весом массой m и лилинейки АВ массы 2m . Кривошип ОС вращается вокруг неподвижной оси Oz , перпендикулярной плоскости чертежа, с угловой скоростью . Найти момент импульса этой системы относительно оси Oz , рассматривая линейку АВ и кривошип

ОС как однородные тонкие стержни, а ползуны А и В - как материаль-

ные точки, если ОС= АС = СВ= l (рис. 15.7). 15.5.2. На поверхности круглого одно-

родного цилиндра радиусом r и массы М, который может вращаться без трения вокруг неподвижной вертикальной оси z , имеется канал в форме винтовой линии; в этом канале находится шарик (материальная точка) массой m . В некоторый момент времени, когда система неподвижна, шарик начинает двигаться по винтовой линии под действием силы тяжести,

224

а цилиндр начинает при этом вращаться вокруг оси z в противоположном направлении. На какой угол повернется цилиндр за то время, в течение которого шарик опустится на расстояние, равное шагу

hвинтовой линии (рис. 15.8).

15.5.3.Сплошной цилиндр радиусом r , положенный, как указано на рис. 15.9, на цилиндрические ролики А и В, вращается с угловой ско-

остановится, если коэффициент трения между цилиндром и роликами равен f , а AOB 2 .

15.5.4. Для быстрого торможения больших маховиков применяется электрический тормоз, состоящий из двух электромагнитов, расположенных диаметрально противоположно и питаемых постоянным током. Токи Фуко, индуцируемые в массе маховика, при его движении около магнитов создают тормозящий момент M1 , пропорциональный скорости v точек обода

неподвижной горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку О. Расстояние от точки О

225

до центра тяжести С диска равно 0,5r (рис. 15.10). Найти закон движения диска при малых колебаниях, а также период этих колебаний. В начальный момент угол отклонения

диска от равновесного положе-

угловая скорость равна нулю.

15.5.6. Для определения коэффициента вязкости жидкости наблюдают колебания диска, подвешенного на упругой вертикальной проволоке в жидкости. К диску приложен переменный момент, равный M sin(pt) (M const ), при котором наблюдается явление резонанса. Момент сопротивления движению диска в жидкости равен S , где - коэффициент вязкости жидкости, S - сумма площадей верхнего и нижнего оснований диска, - его угловая скорость. Определить коэффициент вязкости жидкости , если амплитуда вынужденных колебаний диска при резонансе равна 0 .

15.5.7. Турбина, вал которой параллелен продольной оси судна, вращается с угловой скоростью 10 с-1 минуту: масса вращающихся частей равна m 20 т, а их радиус инерции относительно оси вращения турбины равен 1,5 м. Определить гироскопические давления на подшипники, расстояние между которыми l = 6 м, если судно поворачивается вокруг вертикальной оси на 2 / 12 рад/с.

15.5.8. С концом вертикального вала OO1 , шарнирно соединен горизонтальный стержень ОС, на который свободно насажен массивный цилиндрический каток (бегун). При вращении вала ОО, вокруг вертикальной

оси z бегун катится без скольжения по горизонтальной плоскости, на которую закладывается измельчаемый материал (рис.

226

15.11, а и б). Определить гироскопические реакции в точках О и А, а также усилие в стержне ОС, если заданы масса бегуна m , длина ОС = l, радиус бегуна R и угловая скорость вала

=const.

15.5.9.Диск вращается вокруг неподвижной оси. Центр масс диска лежит на оси вращения. Как изменится главный момент импульса диска, если его угловая скорость увеличится в 2 раза?

15.5.10.Определить главный момент импульса колеса массы M , катящегося по прямолинейному рельсу, если центр

масс диска движется по закону xC at .

15.5.11.Балка А массы M перемещается по горизонтали на двух катушках В и D массы m и радиуса r каждая, катящихся по земле без скольжения. Скорость центра масс каждой из катушек равна v (рис. 15.12).

15.5.12.Определить главный момент импульса кривошип-

но – ползунного механизма, если массы кривошипа и шатуна равны m , масса ползуна равна 0,5m, ОА= АВ= l, кривошип вращается с угло-

вой скоростью .

Рис. 15.13

227

Глава 16. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ

16.1. Кинетическая энергия системы Кинетической энергией системы называется скалярная ве-

личина Т, равная сумме кинетических энергий всех материальных точек системы

Кинетическая энергия имеется в любом движении системы, поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач. Главное отличие кинетической энергии от введенных ранее характеристик

L и K состоит в том, что T является величиной скалярной и неотрицательной. Кинетическая энергия не зависит от направлений движения частей системы и ее центра масс.

Следует помнить, что при определении T можно использовать только скорости материальных точек относительно одной и той же инерциальной системы. Поэтому кинетическая энергия системы тел относительно разных инерциальных систем отсчета оказывается различной.

Отметим еще следующее важное обстоятельство. Внутренние силы действуют на части системы по взаимно противоположным направлениям. По этой причине они, не влияют

на векторные характеристики L и K . Однако внутренние силы могут изменить модули скоростей точек системы, а следо-

вательно, и величину Т. Поэтому от величин L и K , кинетическая энергия системы отличается тем, что ее изменение зависит и от действий внутренних сил в этой системе.

Если система состоит из нескольких тел, то ее кинетическая энергия равна, очевидно, сумме кинетических энергий этих тел.

Получим формулы кинетической энергии тела для разных движений.

228

1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости центра масс тела. Для любой точки vk vC и, согласно (16.1)

где M - масса системы.

Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс и от направления движения не зависит.

Следовательно, кинетическая энергия тела во вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения величина Т не зависит.

3. Плоскопараллельное движение. При этом движении скорости всех точек тела в каждый момент времени распределены так, как если бы тело вращалось вокруг оси, перпендикулярной к плоскости движения и проходящей через мгновенный центр скоростей Р (рис. 16.1). Следовательно, по формуле

229