
Учебное пособие 800360
.pdf
ние с помощью одной только теоремы об изменении кинетической энергии не возможно.
Уравнение (16.13) позволяет решать задачи, в которых в число данных и искомых величин входят: 1) действующие силы; 2) перемещение системы; 3) скорости тел (линейные или угловые) до и после перемещения. При этом действующие силы должны быть постоянными или зависеть только от перемещений (расстояний).
Важно знать, что с помощью теоремы об изменении кинетической энергии можно в случаях, когда положение системы определяется одним параметром, составлять дифференциальные уравнения движения системы и, в частности, находить ускорения движущихся тел. Для этого надо составить уравнение (19.13), продифференцировать обе его части по времени и исключить скорость (см. задачи 16.6, 16.7). При произвольных действующих силах удобнее составлять уравнение движения в виде (16.12), т. е.
в дифференциальной форме (см. задачу
16.8).
Рис. 16.8
Задача 16.4. Стержень АСВ длины 1 подвешен на шарнире в точке А (рис. 16.8). Пренебрегая трением в шарнире А, найти, какую наименьшую угловую скорость , надо сообщить стержню в нижнем положении, чтобы он отклонился до горизонтального положения, имея в этом положении угловую скорость 0.
Решение. В число данных и искомых в задаче величин входят 0 , 1= 0 и перемещение системы, определяемое уг-
лом . Следовательно, для решения задачи удобно воспользоваться теоремой об изменении кинетической энергии. Поскольку тела системы считаются недеформируемыми, (16.14) примет вид
T! T0 Ake . |
(а) |
240

Пусть M - масса стержня. По формулам (16.3) и (12.1) на-
ходим T0 0,5JA 02 Ml2 02 / 6 .
В конечном положении 0 и T1 = 0.
Наложенная на движение стержня связь – шарнир А является идеальной. Поэтому на перемещениях точек стержня совершают работу только активная сила тяжести G Mg и ее
работа |
Ae Gh |
Mgl/ 2. |
|
|
|
|
|
C |
|
|
|
|
|
Тогда Ml2 02 / 6 Mgl/ 2 |
и 0 |
|
|
. |
||
3g / l |
||||||
Задача 16.5. Шкивы А и В, соединенные ремнем (рис. 16.9), вращаются после выключения двигателя так, что шкив А имеет угловую скорость 0 . Общая
масса шкивов равна M , а
Рис. 16.9
вес ремня m. Чтобы затор-
мозить вращение, к шкиву А радиуса R прижимают, с силой Q тормозную колодку. Коэффициент трения колодки о шкив равен f. Пренебрегая трением в осях и считая шкивы сплошными дисками, найти количество оборотов n шкива А до остановки.
Решение. Для определения числа n оборотов воспользуемся уравнением (16.14)
T! T0 Ake . |
(а) |
По условиям задачи T1 0, а T0 TA TB |
TP . Поскольку |
при отсутствии скольжения ремня по шкивам начальные скорости всех точек ремня одинаковы и равны vP0 0R 0BRB ,
по (16.3) и (16.10) получим
TB 0,5(0,5JB ) 02B 0,25mBRB2 02B 0,25mBR2 02 ,
TA 0,5(0,5JA ) 02 0,25mAR2 02 ,
241
TP 0,5mvP20 0,25mR2 02 .
Поскольку M mA mB ,
T0 0,25(M 2m)R2 02 .
Поскольку в конечном положении скорость стержня равна
нулю, T1 0.
В данной системе работа сил тяжести равна нулю, так как центры тяжести колес и ремня при движении системы не перемещаются. Согласно (16.9), работа силы трения FT fQ
AT |
( fQR) 1 fQR2 n. |
|
|
|
|
|
|
|
Из уравнения (а) получаем n (M 2m)R 02 /(8 fQ). |
||||||
|
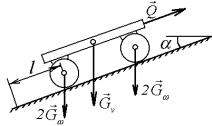
Задача 16.6. Платформу тянут вверх по наклонной плоско- |
||||||
сти, образующей угол = 30 |
с горизонтом, приложив к ней |
||||||
постоянную силу Q = 160 Н (рис. 16.10). Масса поступательно |
|||||||
|
|
движущихся частей платфор- |
|||||
|
|
мы mv 18 кг, массы каждого |
|||||
|
|
из четырех ее сплошных колес |
|||||
|
|
|
m = 2 кг. Колеса катятся без |
||||
|
|
скольжения, |
а сопротивление |
||||
|
|
качению мало. Определить: |
|||||
|
Рис. 16.10 |
|
1) какую поступательную |
||||
|
|
скорость |
v1 |
будет |
иметь |
||
платформа, пройдя путь l 4 м, если v0 = 0; |
|
|
|
||||
|
2) с каким ускорением движется платформа. |
|
|||||
|
Решение. 1) Для определения v1, воспользуемся (16.14) |
||||||
|
T! T0 Ake . |
|
|
|
(а) |
||
|
В данном случае T 0, а T |
T 4T , |
где T 0,5m v2 и |
||||
|
0 |
1 |
v |
|
|
v |
v 1 |
T |
0,75m v2 - кинетические энергии платформы и колеса (см. |
||||||
|
1 |
|
|
|
|
|
|
решение задачи 16.1). Тогда T |
0,5(m |
6m |
)v2 . |
|
|||
|
1 |
|
v |
|
|
1 |
|
242

Работу совершают сила Q и сила тяжести, равная
G (mv 4m )g. Работа силы трения, препятствующей
скольжению, и нормальных реакций плоскости равна нулю.
Тогда A(Q) Ql, A(G ) (mv 4m )gl sin .
Подставляя полученные выражения в (а), получаем
(Q (m |
4m |
)gsin )l 0,5(m |
6m |
)v2 |
, (б) |
||||
|
|
v |
|
|
|
v |
|
1 |
|
откуда v1 |
2(Q (mv |
4m )g sin )l |
2,8 м/с. |
|
|||||
|
|
|
|
|
|||||
|
|
|
mv 6m |
|
|
|
|||
2) Для определения ускорения w будем считать в равенстве (б) величины v1 и l переменными. Величина l определяет положение всей системы и может считаться параметром.
Продифференцировав по времени (б), получим
(Q (m |
4m |
)g sin ) |
dl |
0,5(m |
v |
6m )2v |
dv |
. |
|||||
|
|
||||||||||||
v |
|
|
|
|
|
|
dt |
|
dt |
||||
|
|
dl |
|
|
dv |
|
|
|
|||||
Поскольку |
v , |
w, сокращая на v 0 , получаем |
|||||||||||
|
|
||||||||||||
|
|
dt |
|
dt |
|
|
|
|
|||||
w Q (mv 4m )g sin 0,98 м/с2.
mv 6m
Задача 16.7. На цилиндрический каток радиуса R и массы m намотана нить, перекинутая через блок О (рис. 16.11) и не-
сущая на конце груз D массой mv . Определить скорость vC и
ускорение wC центра С катка в конце пути , если vC0 0 .
Коэффициент трения качения катка равен k , его радиус инерции относительно его оси равен . Массой нити и блока О пренебречь.
Решение. 1) Для определения скорости vC воспользуемся соотношением
243

T! T0 A Aek . |
(а) |
В данном случае T0 0, T T Tv . По формулам (16.2), (16.5) и (12.5) получаем
Tv 0,5mvv2 , T 0,5m vC2 0,5(m 2 ) 2 .
Поскольку точка В является мгновенным центром скоростей, v vA 2vC . Тогда,
T0,5(4mv m (1 2 / R2 ))vC2 .
Работу совершают сила Q и
пара сил (N и m g ). Поскольку
Рис. 16.11 |
v 2vC |
, перемещение груза |
Q равно |
|
h 2 , где - перемещение центра С катка, и A(Q ) mvg2 .
Работа сил сопротивления качению определяется по (16.11). Поскольку N m g const, A MC kN km g / R. То-
гда Ake 2Q km g / R.
Подставляя выражения T и Aв (а), получим
(2Q km g / |
R) 0,5(4m |
m |
(1 2 |
/ R2 ))v2 |
, (б) |
||||
|
|
v |
|
|
C |
|
|||
откуда vC |
|
(2QR km g ) |
|
|
. |
|
|
|
|
|
4m |
R2 m (R2 2 ) |
|
|
|
||||
|
|
v |
|
|
|
|
|
|
|
2) Для определения wC , как и в предыдущей задаче, диф-
ференцируем обе части равенства (б) по t, как по параметру, определяющему положение тел системы. Поскольку vC d / dt , получим
w |
(2QR km g )R |
. |
||
|
||||
C |
4m R2 |
m ( R2 |
2 ) |
|
|
v |
|
|
|
Задача 16.8. Шестерня 1 радиуса r и массы m1 , насаженная на ось, находящуюся на кривошипе ОС 3 длины l и массы m3 , и связанная с ним спиральной пружиной, может пере-
244

катываться по неподвижной шестерне 2 радиуса R l r (рис. 16.12). Момент сил упругости пружины M c , где - угол поворота шестерни 1 относительно кривошипа. Пренебрегая
трением в осях, найти период колеба- |
|
|
ний системы, если ее вывести из по- |
|
|
ложения равновесия. Движения всех |
|
|
частей механизма происходят в гори- |
|
|
зонтальной плоскости. |
Рис. 16.12 |
|
Решение. Определим положение |
||
|
кривошипа углом , отсчитываемым oт оси кривошипа в положении равновесия. Чтобы исключить из рассмотрения неизвестную реакцию оси С, рассмотрим шестерню 1 и кривошип как одну систему и составим дифференциальное уравнение ее движения в виде (16.12).
Сначала определяем кинетическую энергию Т системы, выражая ее через угловую скорость 3 кривошипа, по-
скольку требуется определить закон движения кривошипа
T T3 T1 0,5( J03 2 m1vC2 JC1 12 ).
Считая кривошип однородным стержнем, а шестерню - диском и учитывая, что точка касания является для шестерни 1 мгновенным центром скоростей, получим
J03 ml2 / 3, JC1 0,5m1r2 , vC l , 1 vC / r l / r .
Следует отметить, что в формуле (16.5), по которой вычисляется Т, используются только угловые скорости тел относительно одной и той же системы. Поэтому угловая скорость шестерни определялась относительно колеса, как неподвижного тела, а не относительно кривошипа. Подставляя полученные
выражения в (а), находим T (2m3 9m1 )l2 2 / 12.
При вычислении элементарной работы следует учесть, что внешние силы в данном случае работу не производят и, следо-
вательно, dAe 0. Элементарная работа силы упругости пру-
245

жины (внутренняя сила) при повороте шестерни вокруг кри-
вошипа на угол равна dAi Md c d . Знак минус здесь вызван тем, что, что момент сил упругости на угловом перемещении шестерни совершает отрицательную работу. Для определения закона движения кривошипа выразим угол че-
рез . Поскольку a2b =a1b , R r или (l r) r . Тогда
(l r ) / r и dAi c(1 l / r )2 d .
Поскольку dT dAi ,
|
1 |
(2m 9m )l2 d c(1 l / r )2 d . |
||||||||
|
|
|||||||||
6 |
|
3 |
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
Деля |
обе |
части этого |
равенства на dt, и учитывая, что |
|||||||
d dt |
и d / dt d2 / dt2 , получим дифференциальное |
|||||||||
уравнение движения системы в виде |
||||||||||
|
|
|
|
|
|
d2 |
2 |
|||
|
|
|
|
|
|
|
|
k 0, |
||
|
|
|
|
|
|
dt2 |
||||
где k2 |
6c(l r )2 |
|
- |
постоянная для рассматриваемой |
||||||
(2m |
3 |
9m )l2r2 |
||||||||
|
|
|
|
|
||||||
|
|
|
|
1 |
|
|
|
|
||
системы величина.
Получено дифференциальное уравнение rapмонических колебаний (11.1). Следовательно, кривошип, выведенный из положения равновесия, будет совершать гармонические колебания с периодом
|
2 |
|
2 lr |
|
2m3 9m1 |
. |
|
|
|
||||
|
k l r |
|
6c |
|||
16.5. Потенциальное силовое поле и силовая функция Задачи, рассмотренные в предыдущем параграфе (и в 9.7), решались с помощью теоремы об изменении кинетической энергии потому, что во всех случаях работу действующих сил можно было определить, не зная заранее закона движения сис-
темы. Определим виды сил, имеющих это свойство.
246
Работа на перемещении |
M1M2 силы F , приложенной к |
телу в точке М, вычисляется по формуле (12.12) из 9.4 |
|
M2 |
M2 |
A( M1M2 ) dA |
( Fxdx Fydy Fzdz ). (16.17) |
M1 |
M1 |
Как отмечалось в 9.4, вычислить стоящий справа интеграл, не зная закона движения, т. е. зависимости координат х, у, z от времени t, можно только в случае, когда сила зависит только от положения точки, т. е. от ее координат х, у, z. Про такие силы говорят, что они образуют силовое поле. Силовым полем называется область пространства, в каждой точке которой на помещенную туда материальную частицу действует определенная сила, зависящая от положения частицы.
Примером силового поля служит поле тяготения планет и звезд, а также электрическое поле точечного уединенного электрического заряда. Поскольку сила определяется ее проекциями на оси координат, силовое поле, можно задать уравнениями
Fx 1( x,y,z ),Fy 2( x,y,z ),Fz 3( x,y,z ). (16.18)
Для определения работы таких сил надо в формуле (16.17) все величины под знаком интеграла выразить через один аргумент. Для этого можно использовать зависимости типа y=f (х)
иz= f (х). Эти уравнения, определяют в пространстве уравнение кривой, являющейся траекторией точки М. Следовательно, в общем случае, работа сил силового поля, зависит от траектории, вдоль которой перемещается точка приложения силы.
Пусть выражение, стоящее в (16.17) под знаком интеграла
иопределяющее элементарную работу силы F , является полным дифференциалом некоторой функции U(x,у,z). Тогда
dA dU(x,y,z) или
Fxdx Fydy Fzdz dU( x,y,z ), |
(16.19) |
и работу A( M1M2 ) можно определить, не зная заранее траекто-
рию точки М, а также закон движения.
247
Функция U координат х, у, z, дифференциал которой равен элементарной работе соответствующей силы, называется силовой функцией. Силовое поле, для которого существует силовая функция, называется потенциальным силовым полем, а силы, действующие в этом поле, - потенциальными (консервативными) силами. В дальнейшем силовая функция считается однозначной функцией координат.
Если в формулу (16.17) подставить выражение dA из
(16.19), то
|
M2 |
|
A( M1M2 ) dU( x,y,z ) U2 U1 . |
(16.20) |
|
|
M1 |
|
где U1 U(x1,y1,z1 ), |
U2 U(x2 ,y2 ,z2 ) - значения силовой |
|
функции в точках M1 |
и M2 поля соответственно. |
|
Следовательно, работа потенциальной силы равна разности значений силовой функции в конечной и начальной точках траектории и от вида траектории движущейся точки не зависит. При перемещении по замкнутой траектории U1 U2 и работа потенциальной силы равна нулю.
Основным свойством потенциального силового поля является зависимость работы сил поля при движении в нем материальной точки, только от начального и конечного положений этой точки, а ни от вида траектории, вдоль которой точка перемещается и от закона ее движения.
Силы, работа которых зависит от вида траектории или от закона движения точки приложения силы, называются диссипативными (не потенциальными). К таким силам относятся силы трения и сопротивления сплошных сред - газа, жидкости, а также силы, сопровождающие движение электропроводных тел в переменных электрических и магнитных полях.
Если установлено, что (19.19) выполняется, то силовая функция находится из равенства:
U dA C или U ( Fxdx Fydy Fzdz ) C. |
(16.21) |
Постоянная С здесь может иметь любое значение. Как видно из формулы (16.20), работа от С не зависит. Однако
248

обычно условливаются считать в некоторой точке О, называемой «нулевой точкой», величину U0 0 и определяют С, ис-
ходя из этого условия.
Примерами потенциальных сил являются силы тяжести, упругости и тяготения 9.5). Покажем, что для этих сил действительно существуют силовые функции и определим их. Поскольку под знаком интегралов, из которых в 9.5 были получены формулы (9.14), (9.15) и (9.17), стоят элементарные работы соответствующих сил, то:
1) для силы тяжести, если ось z направлена вертикально вверх, dA= - Pdz. Тогда, считая U 0 при z= 0 (нулевая точка в начале координат), находим:
U mgz. |
(16.22) |
2) для силы упругости, действующей |
вдоль оси Ox, |
dA cxdx . Считая U= 0 при х= 0, находим |
|
U 0,5cx2 . |
(16.23) |
3) для силы тяготения dU kmd(1/r) mgR2d(1/ r ).
Считая, что U 0 при r = (нулевая точка находится в бесконечности) находим
|
|
|
U mgR2/r . |
(16.24) |
где r |
x2 y2 |
z2 |
- расстояние до материальной точки. |
|
Используя выражения для функций U, можно по формуле (16.20) получить те же выражения для работ соответствующих сил (9.14), (9.15) и (9.17) в 9.5.
Зная силовую функцию, можно определить силу, действующую в любой точке поля. По (16.19), определяют дифференциал функции U(x, у, z)
Fxdx Fydy Fzdz U dx U dy U dz.
x y z
Это соотношение должно выполняться при любых дифференциалах координат. Это возможно только при равенстве множителей при дифференциалах одинаковых координат в
249
