Учебное пособие 800360

где JP - момент инерции тела относительно оси, - угловая скорость тела.

Величина JP в формуле (16.4) зависит от положения центра Р, которое при движении тела все время меняется. Вместо JP удобно использовать постоянный момент инерции JC от-

носительно центральной оси. По теореме Гюйгенса (12.4)

JP JC Md2 , где d = PC. Подставим выражение для JP в

(16.4). Учитывая, что точка Р - мгновенный центр скоростей, и, следовательно скорость центра масс С тела vC = * PC d ,

получим

Следовательно, при плоскопараллельном движении кинетическая энергия тела равна сумме его энергии в поступательном движении со скоростью центра масс, и кинетической энергии тела во вращательном движении вокруг центра масс.

4. Общий случай движения. Если за полюс взять центр масс С тела (рис. 16.2), то движение тела в общем случае будет слагаться из поступательного движения со скоростью полюса vC и из вращения вокруг мгновен-

ной оси СР, проходящей через этот полюс. Тогда, в соответствии с теоремой о представлении скоростей тела, в плоском движении, скорость vk любой точки тела равна вектор-

ной сумме скорости полюса vP и

скорости vkP , которую точка получа-

ет при вращении вместе с телом вокруг оси CP

Рис. 16.2

vk vP vkP .

Здесь vkP hk , где hk - расстояние точки k от оси СР, а

- угловая скорость вращения тела вокруг этой оси, опреде-

230

ленная в той же системе отсчета, относительно которой опре-

деляется скорость полюса. Отсюда следует, что

vk2 (vC vkC ) (vC vkC ) vC2 vkC2 2vC vkC.

Поскольку vk hk , из (19.1) следует

T 0,5( mk )vC2 0,5( mkhk2 ) 2 vC mkvkC .

Первая скобка здесь равна массе М тела, а вторая - моменту инерции тела JCP относительно мгновенной оси СР. По-

следняя сумма это импульс тела во вращательном движении вокруг оси СР, проходящей через центр масс тела. Согласно

14.1, mkvkC MvCC 0. Тогда

Следовательно, кинетическая энергия тела в общем случае движения (в частности и при плоскопараллельном движении) равна сумме кинетической энергии поступательного движения со скоростью центра масс, и кинетической энергии вращательного движения вокруг центральной мгновенной оси.

Если за полюс взять не центр масс, а некоторую другую точку А, то для оси, проходящей через эту точку, mkvkA 0,

и выражение для T будет отлично от (16.6) (см. задачу 16.3). Рассмотрим примеры решения задач.

Задача 16.1. Определить кинетическую энергию катящегося без скольжения сплошного цилиндрического колеса массы М, если скорость его центра масс равна vC (рис. 16.6, а).

Решение. Колесо движется плоскопараллельно. По форму-

ле (16.5) или (16.6)

T 0,5MvC2 0,5JC 2 .

Если колесо сплошной однородный цилиндр, то (см. 12.3) JC 0,5MR2 , где R - радиус колеса. С другой стороны, так как точка В является для колеса мгновенным центром скоростей, то vC BC R и vC / R. Тогда

231

T 0,5MvC2 0,25R2vC2 R 2 0,75MvC2 .

Задача 16.2. Относительно горизонтальной направляющей, помеченной штрихами, поступательно со скоростью u движется деталь А. В детали А имеется паз, по которому поступательно со скоростью v перемещается тело В массы М (рис. 16.3). Зная угол , определить кине-

тическую энергию тела В относительно направляющей. Решение. Абсолютное движение тела В будет поступа-

тельным со скоростью w u v , поскольку переносное и относительное движения тела являются поступательными движениями. Тогда

T 0,5Mw2 0,5M(u2 v2 2uvcos ).

Пусть Tr 0,5Mu2 и Te 0,5Mv2 - кинетические энергии тела в относительном и переносном движениях. Очевидно, что Tr Te 0,5Mv2 0,5Mu2 T . Из этого выражения видно, что, если тело совершает сложное движение, то его полная кинетическая энергия не равна в общем случае сумме кинетических энергии тела в относительном и переносном

движениях.

Задача 16.3. Часть механизма состоит из движущейся поступательно

Рис. 16.4 со скоростью u детали (рис. 16.4) и прикрепленного к ней на оси А

стержня АВ длины 1 и массы М. Стержень вращается вокруг оси А (в направлении, указанном дуговой стрелкой) с угловой скоростью . Определить кинетическую энергию стержня в положении, указанном на рисунке.

232

Решение. Стержень совершает сложное (плоскопараллельное) движение. По формуле (16.5) или (16.6)

T 0,5MvC2 0,5JC 2 .

Скорость точки С складывается из скорости u полюса А и

относительной скорости vr , имеющей модуль l / 2 и направленной перпендикулярно отрезку АВ.

Следовательно (рис. 16.4), vC2 u2 v2 2uvcos .

Угловые скорости вращения стержня вокруг точек А и С одинаковы, поскольку угловая скорость вращения тела в плоскопараллельном движении не зависит от выбора полюса. Со-

гласно 12.1 JC Ml2 / 12. Тогда

T 0,5M(u2 0,25 2l2 u lcos ) Ml2 2 / 24

0,5Mu2 0,5Mlu cos Ml2 2 / 6 .

Здесь TP 0,5Mu2 и Tw 0,5JA 2 Ml2 / 6 - кинетические

энергии, которые имело бы тело, совершая только поступательное движение или только вращательное движение относительно точки А. Очевидно, что

TP Tw 0,5Mu2 Ml2 2 / 6 T .

Последний результат означает, что представление кинетической энергии тела, совершающего плоское движение в виде (16.6) возможно, только если момент инерции тела определяется относительно центра масс тела.

16.2. Работа сил, приложенных к системе Работы сил, приложенных к материальной точке, опреде-

ляются по формулам, полученным в 9.4, 9.5. Рассмотрим дополнительно следующие случаи.

1. Работа сил тяжести, действующих на систему. Работа силы тяжести, действующей на частицу массой mk , равна

mk g( zk0 zk1 ), где zk0 и zk1 - начальная и конечная вертикальные координаты положение частицы (см. 9.5). Тогда сумма работ всех сил тяжести, действующих на систему, согласно

233

формулам для координат центра масс, будет равна

AGk zk0 Gk zk1 g mk zk0 g mk zk1

gM( zk0 zk1 ) GhC ,

где M и G - масса системы и суммарная сила тяжести, действующая на систему; hC - вертикальное перемещение центра

масс системы.

Следовательно, работа сил тяжести, действующих на систему, вычисляется как работа их равнодействующей G на перемещении центра масс системы.

вижной оси элементарная работа силы равна произведению вращающего момента силы относительно этой оси на элементарный угол поворота тела относительно этой оси. Формула (16.7) верна и при действии нескольких сил, если считать что

При действии постоянного момента силы

234

Следовательно, при действии силы на вращающееся тело мощность равна произведению вращающего момента силы на угловую скорость тела. При той же самой мощности вращающий момент будет тем меньше, чем больше угловая скорость.

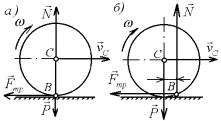
3) Работа сил трения, действующих на катящееся тело. На колесо радиуса R (рис. 16.6), катящееся по некоторой поверхности без скольжения, дей-

ствует сила трения FT ,

является мгновенным центром скоростей и vB = 0. Поскольку

d B vBdt, d B 0 и dA 0.

Следовательно, при качении без скольжения, работа силы трения, препятствующей скольжению, на любом перемещении тела равна нулю. Если считать тела недеформируемыми, а си-

лу нормальной реакции N приложенной в точке В, то работа

нормальной реакции N также будет равна нулю. Сопротивление качению, возникает вследствие деформа-

ций поверхностей (рис. 16.6, б), за счет которых возникает па-

ра сил (N , G ) с моментом M kN , где k - коэффициент трения качения.

235

нуля. Примером может служить явление отдачи (отката) орудий, при котором внутренние силы давления, действующие и на снаряд и на откатывающиеся части орудия, совершают положительную работу. Сумма этих работ положительна, и изменяет кинетическую энергию системы от величи-

ны T= 0 до выстрела до ве-

личины T 0 в конце выстрела.

1) Неизменяемая система. Неизменяемой называют систему, в которой расстояния между точками приложения внутренних сил во время движения системы не изменяются. Такими системами являются абсолютно твердое тело или нерастяжимая нить.

Пусть две точки B1 и B2 неизменяемой системы (рис. 16.7), действующие друг на друга с силами F12i и F21i , имеют в данный момент скорости v1 и v2 . Тогда, за промежуток вре-

Поскольку отрезок B1B2 , не изменяет свою длину, то по из-

вестной теореме кинематики проекции векторов v1 и v2 , а

следовательно, и перемещений dr1 и dr2 на направление отрезка B1B2 , будут равны друг другу, т. е. B1B1 B2B2 . Тогда модули элементарных работ сил F12i и F21i будут одинаковы, а их знаки - противоположны и в сумме дадут нуль. Этот результат верен для всех внутренних сил при любом перемещении системы.

Следовательно, для неизменяемой системы сумма работ всех внутренних сил равна нулю и (16.12) или (16.13) принимают вид

237

2) Система с идеальными связями. Пусть на систему, наложены связи, не изменяющиеся со временем. Разделим все действующие на точки системы внешние и внутренние силы на активные и реакции связей. Тогда уравнение (16.12) примет вид

dT dAka dAkr ,

где dAka - элементарная работа внешних и внутренних актив-

ных сил, действующих на точку k системы, а dAkr - элемен-

тарная работа реакций внешних и внутренних связей, наложенных на ту же точку.

Как видно, изменение кинетической энергии системы зависит от работы и активных сил и реакций связей. Однако можно ввести понятие о таких механических системах, для которых связи не изменяют кинетическую энергию системы при ее движении. Для таких связей должно выполняется условие

Если для не изменяющихся со временем связей, сумма работ всех реакций при элементарном перемещении системы равна нулю, то такие связи называют идеальными. Существует несколько видов идеальных связей.

В 9.6 было установлено, что если связью является неподвижная поверхность (или линия), трением о которую можно пренебречь, то при скольжении тела вдоль такой поверхности

(линии) работа реакции N равна нулю.

В 16.2 было показано, что если пренебречь деформациями, то при качении без скольжения тела по шероховатой поверх-

ности работа нормальной реакции N и силы трения FT , т. е. касательной составляющей реакции, равна нулю.

Работа реакции R любого шарнира, если пренебречь трением и зазором, будет также равна нулю, поскольку точка

238

приложения силы R при любом перемещении системы неподвижна.

Если материальные точки B1 и B2 (рис. 16.7), рассматри-

вать как связанные жестким (недеформируемым) стержнем B1

B2 , то силы F12i и F21i будут реакциями стержня. Работа каждой из этих реакций при перемещении системы не равна нулю, но сумма этих работ равна нулю. Таким образом, все рассмотренные связи с учетом перечисленных оговорок можно считать идеальными.

Для механической системы, на которую наложены только

Таким образом, изменение кинетической энергии системы с идеальными постоянными связями при любом ее перемещении равно сумме работ на этом перемещении, всех приложенных к системе внешних и внутренних активных сил.

Все предыдущие теоремы позволяли исключить из уравнений движения внутренние силы, но все внешние силы, в том числе и заранее неизвестные реакции внешних связей, в уравнениях сохранялись. Теоремы об изменении кинетической энергии важна потому, что при постоянных идеальных связях она позволяет исключить из уравнений движения все заранее неизвестные реакции связей.

16.4. Решение задач Теоремой об изменении кинетической энергии удобно

пользоваться в тех случаях, когда движущаяся система является неизменяемой. В этих случаях теорема позволяет исключить из рассмотрения все неизвестные внутренние силы, а при постоянных связях и неизвестные реакции внешних связей.

В случае изменяемой системы теорема дает решение задачи только тогда, когда внутренние силы заранее известны. В противном случае (см. задачи 13.1, 14.2 и др.) получить реше-

239