
Основы механики. Рябцев В.А., Воропаев А.А
.pdf
В. А. Рябцев, А. А. Воропаев, Д. В. Хван
ОСНОВЫ МЕХАНИКИ
Учебное пособие
Воронеж 2018
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования «Воронежский государственный
технический университет»
В. А. Рябцев, А. А. Воропаев, Д. В. Хван
ОСНОВЫ МЕХАНИКИ
Учебное пособие
Утверждено учебно-методическим советом университета в качестве учебного пособия
Воронеж 2018
УДК 531
ББК 22.1я7 О-753
Рецензенты:
кафедра социально-гуманитарных, естественнонаучных и общеобразовательных дисциплин филиала РГОТУПС (г. Воронеж)
(зав. кафедрой канд. техн. наук, доц. О. А. Лукин); канд. техн. наук, доц. Ю. Б. Рукин
Рябцев, В. А.
Основы механики: учеб. пособие [Электронный О-753 ресурс]. - Электрон. текстовые и граф. данные (1,9 Мб) / В. А. Рябцев, А. А. Воропаев, Д. В Хван. - Воронеж: ФГБОУ ВО «Воронежский государственный технический университет», 2018.- 1 электрон. опт. диск (СD-ROM): цв. – Систем. требования: ПК 500 и выше; 256 Мб ОЗУ; Windows ХР; SVGA с разрешением 1024x768; Adobe
Acrobat; CD-ROM дисковод; мышь. - Загл. с экрана.
ISBN 978-5-7731-0722-4
В учебном пособии рассмотрены краткие сведения по разделам статики и кинематики и подробно рассмотрен раздел динамики. Приведено много примеров решения задач и подборка задач для самостоятельного решения.
Издание соответствует требованиям Федерального государственного образовательного стандарта высшего образования по направлению подготовки 16.03.01 «Техническая физика» (профиль «Физическая электроника»), дисциплине «Механика».
Предназначено для студентов очной формы обучения. Ил. 182. Табл. 1. Библиогр.: 7 назв.
|
УДК 531 |
|
ББК 22.1 я7 |
ISBN 978-5-7731-0722-4 |
Рябцев В. А., Воропаев А. А., |
|
Хван Д. В., 2018 |
|
ФГБОУ ВО «Воронежский |
|
государственный технический |
|
университет», 2018 |
ВВЕДЕНИЕ
В данном учебном пособии содержатся основные сведения по дисциплине «Механика» для направления подготовки 16.03.01 «Техническая физика» профиля «Физическая электроника».
За основу принят традиционный способ изложения: сначала формулируются основные теоретические положения, а затем, рассматриваются общие методы решения различных типовых задач, с которыми бакалавр может встретится в своей работе.
Поскольку разделы кинематика и статика входят в курс общей физики, эти разделы изложены в данном учебном пособии как справочный материал, максимально кратко – без выводов, примеров и задач для самостоятельного решения. Разделы классической динамики точки, системы и твердого тела изложены достаточно подробно.
Для лучшего усвоения теоретических положений изложение каждого раздела теории, начиная с гл. 8, сопровождается примерами решения типовых задач, выполненными в алгебраическом, а затем в числовом, виде. В конце глав 8-17 приведены подборки задач для самостоятельного решения. Учебное пособие вполне применимо для самостоятельного изучения.
Все величины измеряются в Международной системе единиц измерения (СИ).
Приведен список дополнительной литературы для дальнейшего изучения.
Авторы будут благодарны читателям, которые сообщат на кафедру прикладной математики и механики свои пожелания и критические замечания для учета в дальнейшей работе по совершенствованию данного учебного пособия и преподавания указанных курсов.
3
Глава 1. КИНЕМАТИКА ТОЧКИ
1.1. Основные понятия Раздел «Кинематика» является частью дисциплины «Тео-
ретическая механика».
Теоретическая механика относится к физико - математическим наукам. Она служит теоретической базой для многих технических дисциплин, например сопротивления материалов, теории механизмов и машин, деталей машин и других, без знания которых немыслимо стать специалистом в современной технике.
Важнейшими для всей теоретической механики являются две абстракции: материальная точка и абсолютно твердое тело.
Материальной точкой называют тело, обладающее конечной или бесконечно малой массой, размеры которого в рассматриваемом явлении несущественны.
Жесткой системой материальных точек, называют такую систему (совокупность) материальных точек, для которой расстояния между любыми двумя точками постоянны. Частным случаем такой системы является абсолютно твердое (жесткое) тело, точки которого полностью или частично заполняют некоторую область пространства.
Если несколько твердых тел образуют между собой подвижные соединения, то эти тела в технике называю звеньями.
Если при заданных движениях одного или нескольких звеньев другие звенья совершают закономерные движения, то такое соединение звеньев называется механизмом.
В природе и технике не существуют ни материальные точки, ни абсолютно твердые тела. Абстракцией «материальная точка» можно пользоваться при описании явлений, в которых формы и размеры тела несущественны, но необходимо учесть массу тела, например, при изучении падения тел в вакууме, при вычислении кинетической энергии тела в поступательном движении и т.д. Во всех подобных случаях тело заменяется одной
4
из точек этого тела. Обычно за эту точку принимают центр масс тела, считая, что в ней сосредоточена масса всего тела.
Абстракция «абсолютно твердое тело» используется в тех явлениях, для которых масса, форма и размеры тела существенны, но изменения формы - деформации настолько малы, что ими можно пренебречь. На такой абстракции основана, например, вся аэрогидромеханика, так как аэро- и гидродинамические силы сильно зависят от размеров и формы движущихся телсамолетов, кораблей и подводных лодок. Следовательно, самолеты и корабли должны быть настолько жесткими, чтобы неизбежно возникающие при их движении деформации были малыми и не влияли существенно на аэродинамические силы, например на лобовое сопротивление или подъемную силу самолета. Важно понимать, что не зная размеров тела, приобретенных вследствие его деформаций, нельзя составить даже уравнения равновесия тела, нельзя определить действующие внутри тела силы и моменты, по которым можно было бы найти деформации этого тела. Замкнутый круг проблем исследования равновесия или движения деформируемого тела разрывается так, что при определении реакций опор на жесткие тела в технике малыми деформациями этих тел пренебрегают. Если же нужно учесть влияние деформаций тела на действующие на него реакции других тел, то используют метод последовательных приближений, многократно повторяя процесс определения реакций и деформаций тела.
1.2.Способы задания движения точки
Вкинематике независимой переменной (аргументом) является время t. Все другие величины – перемещения, координаты, скорости и ускорения являются функциями времени.
Механическим движением называют изменение во времени положения в пространстве точек и тел относительно какого
-либо основного тела, с которым связана система отсчета. Кинематика изучает механическое движение точек и тел независимо от причин, вызывающих эти движения. Всякое движение,
5

как и покой, относительно и зависит от выбора системы отсчета.
Траекторией точки называют линию, описываемую движущейся точкой. Если траектория - прямая линия, то движение точки называют прямолинейным, а если - кривая, то криволинейным. Если траектория - плоская, то движение точки называют плоским. Движение точки или тела, считается заданным или
известным, если для каждого момента времени можно указать положение точки или тела относительно выбранной системы отсчета.
При изучении кинематики движение точки можно задавать следующими тремя способами.
1.2.1. Векторный способ
Положение точки M определяется заданием векторарадиуса r этой точки как функции скалярного аргумента t
r r(t ) |
(1.1) |
Модуль и направление вектора - радиуса r , имеющего начало в неподвижной точке О (полюсе) и конец в точке M, в общем случае меняется (рис. 1.1). Конец вектора - радиуса описывает траекторию точки M.
1.2.2. Координатный способ Если поместить начало декартовых координат в начале
вектора-радиуса r , то координаты точки M - конца r будут равны проекциям r на оси координат: rx = x; ry = y; rz = z.
Пусть i , j,k - единичные векторы (орты) осей координат. То-
6
гда, вектор - |
радиус r можно записать |
в виде |
r rxi ry j rzk |
или, в данном случае, |
|
|
r xi yj zk . |
(1.2) |
Положение точки определяется тремя уравнениями движе- |
||
ния в координатном виде |
|
|
|
х = х(t), у = у (t), z = z(t). |
(1.3) |
Эти выражения задают закон движения точки и являются уравнениями траектории в параметрическом виде. Для получения уравнения траектории в непараметрическом виде, надо из (1.3) исключить параметр - время t.
Если рассматривается плоская траектория, т. е. считается, что движение точки происходит в плоскости ху, то z= 0 и вме-
сто (1.1) и (1.2) получаем |
|
|
r xi |
yj , |
(1.2’) |
х = х(t), у = у (t). |
(1.3’) |
|
1.2.3. Естественный способ Положение точки в пространстве определяется заданием:
а) траектории точки; б) криволинейной координаты = O1M точки М, отсчитываемой вдоль траектории и начала O1 ее отсчета (см. рис. 1.1); в) направления положительного отсчета координаты ; г) уравнения или закона движения точки по траектории
= (t). |
(1.4) |
1.3.Скорость точки
Взависимости от способа задания движения скорость точки выражается в трех различных видах.
1.3.1.Векторный способ
Мгновенной скоростью точки называют вектор v , равный первой производной от вектора - радиуса точки по времени
7
v |
lim |
r |
|
dr |
. |
(1.5) |
|
|
|||||
|
t 0 t |
|
dt |
|
||
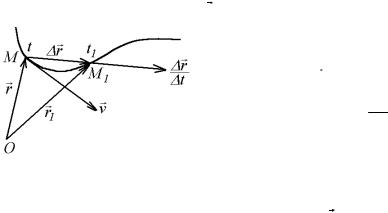
На рис. 1.2 моменту времени t соответствует вектор-радиус
r , моменту t1 = t + t - вектор - радиус r1 r r , где приращение вектора - радиуса (переме-
щение) r MM1.
При t 0 вектор r будет
t
поворачиваться вокруг точки M,
Рис. 1.2 и в пределе секущая MM1 к траектории превращается в каса-
тельную. При этом расстояние между точками M и M1 стре-
мится к нулю. Следовательно, вектор скорости v направлен по касательной к траектории в сторону движения точки.
1.3.2. Координатный способ
Представляя r в виде (1.2), подставляя r в (1.5) и, учитывая, что единичные векторы являются постоянными величинами и, выносятся их за знаки производных, получаем
|
|
dr |
|
dx |
dy |
dz |
|
|||
v |
|
|
|
|
i |
|
j |
|
k . |
(1.6) |
t |
|
|
|
|||||||
|
|
|
dt |
dt |
dt |
|
||||
Как и любой вектор, вектор скорости точки может быть представлен в виде суммы
v vxi vy j vzk . |
|
|
|
(1.7) |
|||||
Следовательно, |
|
|
|
|
|
|
|
||
vx |
dx |
; |
vy |
dy |
; vz |
|
dz |
. |
(1.8) |
|
|
|
|||||||
|
dt |
|
dt |
|
dt |
|
|||
Итак, проекция вектора скорости точки на неподвижную |
|||||||||
ось координат равна первой производной по времени от соответствующей координаты точки.
Модуль и направление вектора скорости определяются формулами
8
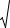
|
|
|
|
|
|
|
|
|
|
|
vx |
|
||
|
|
|
2 |
2 |
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||
v |
v |
|
vx |
vy |
vz |
, |
cos(v,x) |
|
|
|
, |
|||
|
v |
|||||||||||||
|
|
|
|
|
|
vy |
|
|
|
|
v |
|
||
|
|
|
|
|
|
|
|
z |
|
|
||||
|
|
|
cos(v,y) |
|
, |
|
cos(v,z ) |
|
|
|
(1.9) |
|||
|
|
|
|
|
|
|
|
|||||||
vv
1.3.3.Естественный способ
По определению скорость точки направлена по касательной к траектории, а ее проекция на вспомогательную ось задается формулой
v |
|
d |
|
|
|
dt . |
(1.10) |
||||
|
|
||||
Размерность скорости точки: |
[v] длина/ время, напри- |
||||
мер м/с. Если точка движется в сторону увеличения криволи-
нейной координаты , то d |
> 0, и, следовательно, |
v |
> 0. В |
|||||
противном случае d < 0 и v < 0. |
|
|
|
|||||
Движение точки называют равномерным, если величина |
||||||||
скорости постоянна v |
|
d |
|
const . Отсюда d = |
v |
dt. Ин- |
||
dt |
||||||||
|
|
|
|
|
|
|||
тегрированием получаем |
|
|
|
|
||||
d v dt v dt; |
v t C , |
|
|
|||||
где C - произвольная постоянная интегрирования |
|
|
||||||
Пусть начало отсчета O1 |
на траектории таково, что при t0 = |
|||||||
0 0 |
= 0. Из последнего равенства следует C = 0. Тогда =v t |
|
или |
v / t . |
(1.11) |
|
||
|
Интегрирование (1.10) дает |
|
|
t |
|
|
v dt. |
(1.12) |
|
0 |
|
|
Если известна функция v =v (t), |
то по этой формуле |
можно найти закон движения в виде (1.4), |
|
|
|
9 |
|
