1.4. Монотонные последовательности
1. Определение и признак сходимости монотонных последовательностей.
Определение.
Последовательность
называется возрастающей,
если
для всех n;
неубывающей, если
для всех n;
убывающей, если
для всех n;
невозрастающей,
если
для всех n.
Все такие последовательности объединяются общим названием: монотонные последовательности. Возрастающие и убывающие последовательности называются также строго монотонными.
Рассмотрим примеры монотонных последовательностей.
1. Последовательность 1, 1/2, 1/3, . . , 1/n, . . . убывающая и ограниченная.
2. Последовательность 1, 1, 1/2, 1/2, 1/3, 1/3, . . . 1/n, 1/n, . . . невозрастающая и ограниченная.
3. Последовательность 1, 2, 3, . . . n, . . . возрастающая и неограниченная.
4. Последовательность 1, 1, 2, 2, 3, 3, . . . n, n, . . . неубывающая и неограниченная.
5. Последовательность 1/2, 2/3, 3/4, . . ., n/(n+1), . . . возрастающая и ограниченная.
Отметим, что
монотонные последовательности ограничены,
по крайней мере, с одной стороны:
неубывающая последовательности – снизу
(
для всех n),
невозрастающие – сверху (
для всех n).
Оказывается, что если монотонная
последовательность ограничена с обеих
сторон, т. е. просто ограничена, то она
сходится. Немонотонные последовательности
этим свойством не обладают. Например,
немонотонная последовательность
ограничена, но не сходится (см. замечание
к теореме 2 из п. 1.2). Имеет место следующая
основная теорема о монотонных
последовательностях.
Теорема. Монотонная ограниченная последовательность сходится.
З а м е ч а н и е. Ограниченность монотонной последовательности является необходимым и достаточным условием сходимости. В самом деле, если монотонная последовательность ограничена, то в силу сформулированной теоремы она сходится; если же монотонная последовательность сходится, то по теореме 2 из п. 1.2 она ограничена.
2. Число е.
Рассмотрим последовательность
с общим
членом
:
.
Докажем, что она сходится. Для этого достаточно доказать, что последовательность - возрастающая и ограничена сверху. Применив формулу бинома Ньютона, получим
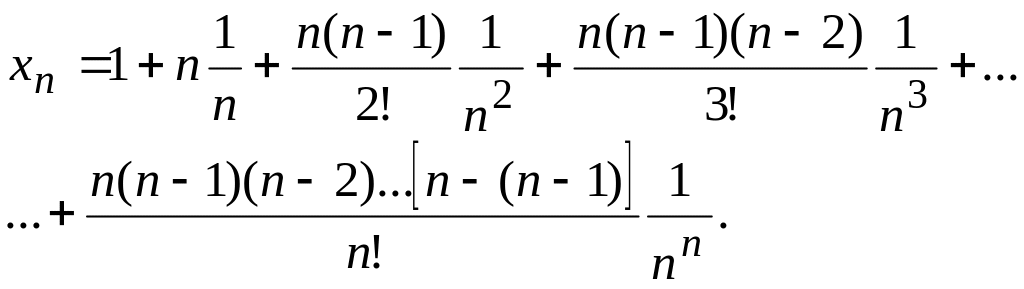
Представим это выражение в следующей форме:
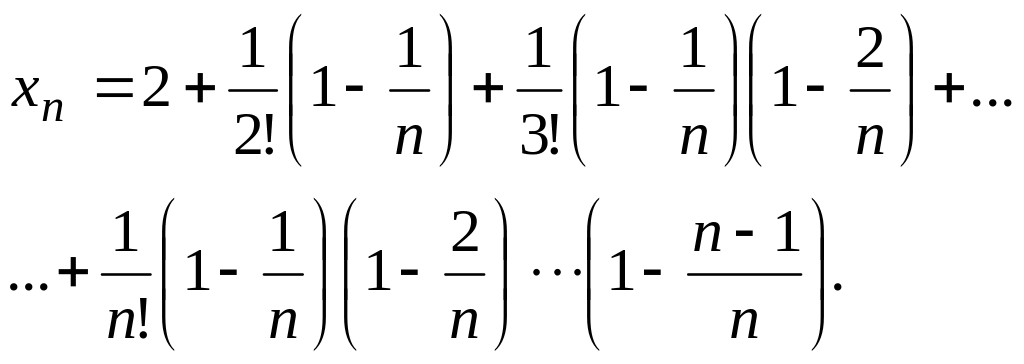(1.6)
Аналогичным образом
представим
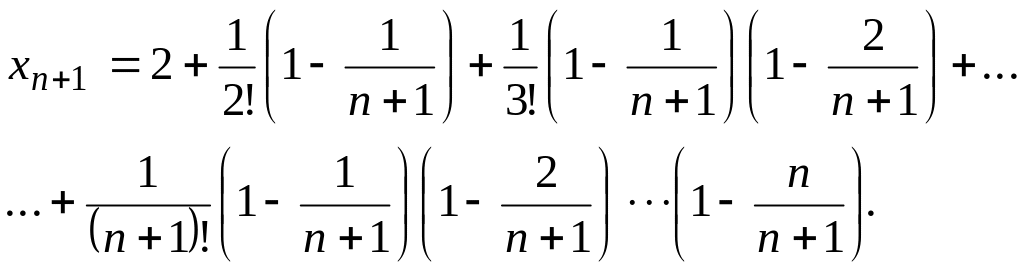
Заметим теперь,
что
<
при
.
Поэтому каждое
слагаемое в выражении для
больше соответствующего слагаемого в
выражении для
и, кроме того, у
по сравнению с
добавляется еще одно положительное
слагаемое. Следовательно,
<
,
т.е. последовательность
возрастающая.
Для доказательства ограниченности сверху данной
последовательности
заметим, что каждое выражение в круглых
скобках в соотношении (1.6) меньше единицы.
Учитывая также, что
при
,
получаем
Используя формулу
суммы геометрической прогрессии, придем
к неравенству
< 3.
Таким образом,
доказано, что последовательность
возрастающая и ограничена сверху. По
теореме она имеет предел. Этот предел
обозначают буквой е.
Итак, по определению,
Отметим, что число
е играет большую роль во многих вопросах
математики. Оно, в частности, является
основанием натуральных логарифмов.
Отметим, что так как
и из (1.6)
непосредственно очевидно, что
,
то число е
заключено
в пределах
.
Доказано, что число е
иррациональное.