Формула Тейлора.
Теорема
6 (теорема
Тейлора).
Пусть функция
имеет в точке а и в некоторой ее
окрестности производные порядка n+1.
Пусть х – любое значение аргумента из
указанной окрестности,
.
Тогда между точками а и х найдётся
точка
такая,
что справедлива следующая формула:
(4.3)
Формула
(4.3) называется формулой
Тейлора, а
выражение
остаточным
членом в форме Лагранжа.
Его можно переписать в другом виде. Так
как точка (а,
х),
то найдётся такое число
из интервала
, что
= а+q
(х
а), и остаточный
член принимает вид
Или,
если функция
ограничена в окрестности точки а,
то
при
В этом случае говорят, что остаточный
член записан
в форме Пеано.
2.
Формула Маклорена.
Формулой Маклорена называют формулу
Тейлора (4.3) при
:
Остаточный член имеет вид:
1)
в форме Лагранжа
2)
в форме Пеано
3. Разложение некоторых элементарных функций по формуле Маклорена.
1)
Так
как
то формула Маклорена имеет вид
(4.4)
2)
Так
как
то формула Маклорена имеет вид
(4.5)
3)
Так
как
то формула Маклорена имеет вид
(4.6)
В
формуле (4.5) остаточный член записан в
виде
а не в виде
так как следующий за последним член
равен нулю (то же самое относится к
формуле (4.6)).
4)
,
где
вещественное число. Так как
то формула Маклорена имеет вид
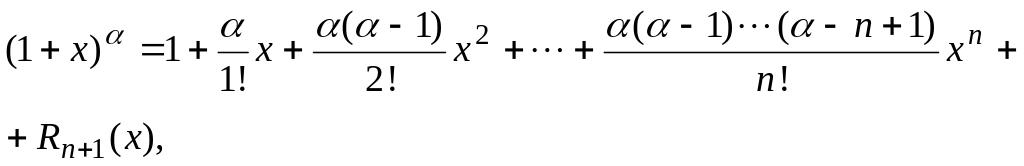
где остаточный член в форме Лагранжа равен
В
частном случае, когда
натуральное число,
следовательно,
и мы получаем известную из элементарной
математики формулу
бинома Ньютона
(4.7)
Приведенные выше разложения показывают, что с помощью формулы Маклорена функции можно с определённой степенью точности заменять многочленами, являющимися наиболее простыми элементарными функциями. Над многочленами удобно выполнять арифметические действия, нетрудно вычислить значение многочлена в любой точке и т.д.
Формулы Тейлора и Маклорена позволяют приближённо заменять многочленами и более сложные функции. Кроме того, эти формулы имеют широкий круг приложений.
4. Использование формулы Маклорена для вычисления пределов. Формула Тейлора является эффективным средством для вычисления пределов функций, с которыми часто приходится иметь дело при исследовании функций.
Пример
1. Найти
Решение.
По формуле (4.5)
при
имеем
Пример
2. Найти
Решение. По формулам (4.4), (4.5) и (4.6) имеем
.
(здесь
символом
обозначена
величина
являющаяся бесконечно малой при
).
4.4. Исследование поведения функций и построение графиков
1. Признак монотонности функции.
Теорема
1. Если
функция
дифференцируема на интервале
и
(
)
на
,
то функция
не убывает (не
возрастает)
на
.
Если
(
)
на
,
то функция
возрастает (убывает)
на
.
2. Отыскание точек локального экстремума функции.
Определение.
Точка
называется точкой строгого локального
максимума (минимума)
функции
,
если для всех x из некоторой -
окрестности точки
выполняется неравенство
(
)
при
(рис. 19).
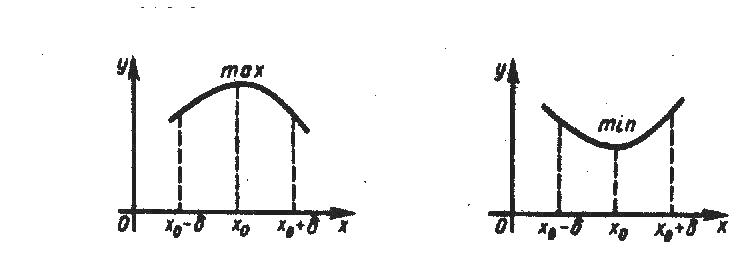
Рис. 19
Локальный максимум (max) и локальный минимум (min) объединяются общим названием локальный экстремум.
Из определения следует, что понятие экстремума носит локальный характер в том смысле, что неравенство ( ) может и не выполняться для всех значений х в области определения функции, а должно выполняться лишь в некоторой окрестности точки . Очевидно, функция может иметь несколько локальных максимумов и несколько локальных минимумов, причем может так случится, что иной локальный максимум окажется меньше какого-то локального минимума.
Теорема
2 (необходимое
условие локального экстремума).
Если функция
имеет в точке
локальный экстремум и дифференцируема
в этой точке, то
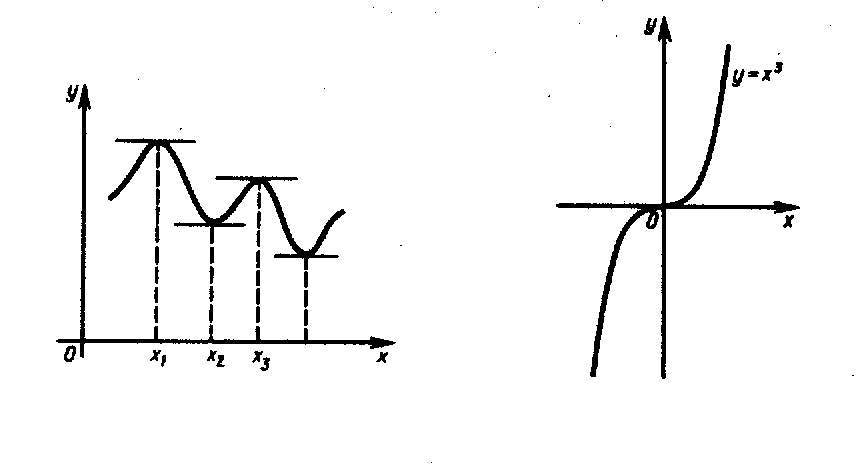
Рис. 20 Рис. 21
Теорема
2 имеет следующий геометрический смысл.
Если
точки локального экстремума и в
соответствующих точках графика существуют
касательные, то эти касательные
параллельны оси
Ох (рис. 20).
Иногда
такие точки называют стационарными; мы
будем называть их точками
возможного экстремума.
Если точка
точка возможного экстремума, т.е.
то она может и не быть точкой локального
максимума или минимума. Например, если
то
при
,
но, тем не менее, в точке
нет локального экстремума (рис. 21).
Установим достаточное условие существования локального экстремума. Этому посвящается следующая теорема.
Теорема
3
(достаточное
условие локального экстремума).
Пусть
функция
дифференцируема в некоторой -окрестности
точки
.
Тогда,
если
(
)
для всех х
из
а
(
)
для всех х
из
то в точке
функция
имеет локальный максимум (минимум);
если же
во всей -окрестности
точки
имеет один и тот же знак,
то в точке
локального экстремума нет.
Другими
словами, если
при переходе через точку
меняет знак с «»
на «»,
то
точка локального максимума; если
в точке
меняет знак с «»
на «»,
то
точка локального минимума; если же
в точке
знака не меняет, то в точке
экстремума не существует.
З
а м е ч а н и е. Теорема 3 остаётся
справедливой, если функция
в самой точке
не дифференцируема, а только непрерывна.
Так, например, функция
в точке
непрерывна, но не дифференцируема.
В
качестве примера рассмотрим вопрос об
отыскании точек локального экстремума
функции
.
Находим производную
.
Решая
уравнение
,
получаем две точки возможного экстремума:
и
.
Дальнейшее исследование удобно вести,
нарисовав вспомогательный чертеж (рис.
22).
Отметим на нем точки
и
и
Р
ис.
22
определив знак в окрестности этих точек, получаем: в точке имеет локальный максимум, а в точке
локальный
минимум. Далее находим:
,
На рис. 22 видны и интервалы монотонности : (,1), (1, 1) и (1,), причем в первом и третьем из них функция возрастает, а во втором – убывает.
3.
Направление выпуклости и точки перегиба
графика функции. Пусть
функция
дифференцируема на интервале
.
Тогда существует касательная к
графику функции
в любой
точке
этого графика (
),
причем касательная не параллельна оси
Оу,
поскольку ее угловой коэффициент, равный
,
конечен.
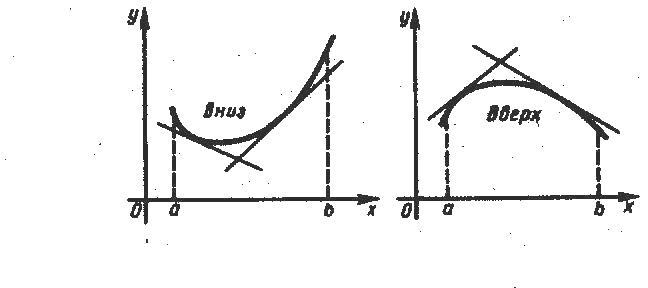
Рис. 11
Рис. 11
Рис. 23
Определение 1. Будем говорить, что график функции имеет на выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на (рис. 23).
Теорема
4.
Если функция
имеет на интервале
вторую
производную и
во всех точках
,
то график функции
имеет на
выпуклость, направленную вниз (вверх).
Определение
2. Точка
М(
)
называется точкой перегиба графика
функции
,
если в точке М график имеет касательную,
и существует такая окрестность точки
,
в пределах которой график функции
слева и справа от точки
имеет разные направления выпуклости.
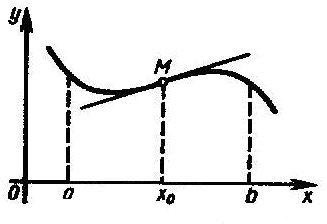
Рис. 24
Очевидно, что в точке перегиба касательная пересекает график функции, так как с одной стороны от этой точки график лежит под касательной, а с другой – над нею, т.е. в окрестности точки перегиба график функции геометрически переходит с одной стороны касательной на другую и «перегибается» через неё. Отсюда произошло название «точка перегиба» (рис. 24).
Теорема
5
(необходимое
условие точки перегиба).
Пусть график
функции
имеет перегиб в точке М(
)
и пусть функция
имеет в точке
непрерывную вторую производную.
Тогда
в точке
обращается в нуль,
т.е.
.
Следует заметить, что не всякая точка М( ), для которой , является точкой перегиба.
Н
апример,
график функции
не имеет перегиба в точке (0; 0), хотя
при
(рис. 25).
Поэтому равенство нулю второй производной является лишь необходимым условием перегиба.
Точки М( ) графика, для которых , будем называть критическими.
Необходимо дополнительно исследовать вопрос о наличии перегиба в каждой критической точке, для чего следует установить достаточное условие перегиба.
Теорема
6
(достаточное
условие точки перегиба).
Пусть функция
имеет вторую производную в некоторой
окрестности точки
.
Тогда, если в пределах указанной
окрестности
имеет разные знаки слева и справа от
точки
,
то график
имеет перегиб в точке М(
).
З
а м е ч а н и е. Теорема остаётся верной,
если
имеет вторую
производную в некоторой окрестности
точки
,
за исключением самой точки
,
и существует касательная к графику
функции в точке М.
Тогда, если в пределах указанной
окрестности
имеет разные знаки слева и справа от
точки
,
то график функции
имеет перегиб
в точке М(
).
Рассмотрим
пример:
.
Эта функция в точке
имеет
бесконечную производную, а касательная
к графику функции в точке О(0;
0) совпадает с осью Оу.
Вторая производная в точке
не существует. Однако график функции
имеет перегиб в точке
,
так как вторая производная
имеет слева и справа от точки
разные знаки (рис. 26).
Итак, вопрос о направленности выпуклости и точках перегиба графика функции исследуется с помощью второй производной.
В
качестве примера возьмем функцию
которую начали рассматривать в п. 2. Знак
второй производной будем отмечать
на вспомогательном чертеже, изображенном
на рис. 22. Находим вторую производную:
Из уравнения 6х
= 0 получаем
одну критическую
т
очку:
.
Отметив точку
на вспомогательном чертеже (рис. 27) и
определив знак
в ее окрестности, получаем: слева от
точки
<0
(выпуклость графика направлена вверх),
а справа
>0
(выпуклость графика направлена вниз),
т.е. точка
является точкой перегиба графика
рассматриваемой функции. Этот график
схематически изображен на рис. 28.
4. Асимптоты графика функции. При исследовании поведения функции на бесконечности, т. е. при х и при х или вблизи точек разрыва второго рода, часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называют асимптотами. Существуют три вида асимптот: вертикальные, горизонтальные и наклонные.
Определение
1. Прямая
называется
вертикальной асимптотой графика функции
,
если хотя бы одно из предельных значений
или
равно
или .
В
этом случае расстояние от точки
до прямой
равно
и, следовательно, d 0 при х .
Например,
график функции
(рис. 29) имеет
вертикальную асимптоту
,
так как
при х
0
и
при х
0 .
Определение
2.
Прямая
называется горизонтальной асимптотой
графика функции
при
(
),
если
.
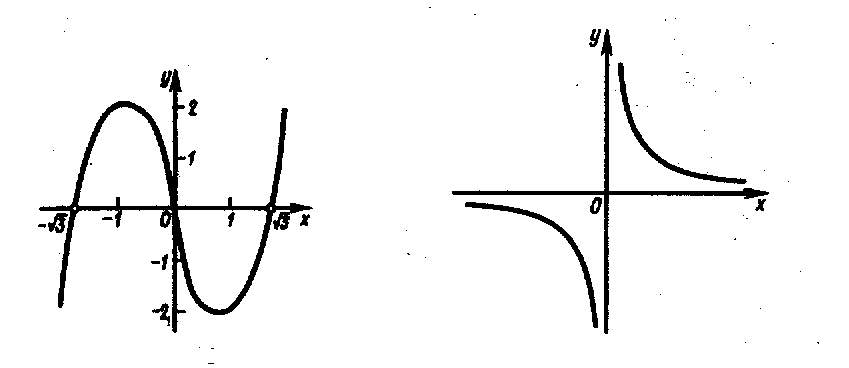Рис.
28
Рис. 29
В этом случае расстояние от точки до прямой равно
и,
следовательно,
при
,
так как,
.
Например,
график рассмотренной выше функции
имеет горизонтальную асимптоту
при
и при
,
так как
0
при
и при
.
Определение
3. Прямая
(
)
называется наклонной асимптотой графика
функции
при
(
),
если функцию
можно представить в виде
(4.8)
где
при
(
).
Рассмотрим геометрический смысл наклонной асимптоты. Для определенности разберем случай, когда . (Случай рассматривается аналогично).
Пусть
– точка
графика функции
и пусть прямая
является наклонной асимптотой графика
функции при
.
Текущую ординату точки на асимптоте
обозначим через
,
точку на асимптоте – через
(рис.30).Тогда
при
.
Опустим из точки М
перпендикуляр
МР на
асимптоту. Расстояние d
от точки М
до асимптоты равно
где
угол между асимптотой и осью Ох,
и, следовательно,
.
Таким образом, расстояние от точки графика функции до асимптоты стремится к нулю при х+, т.е. график функции неограниченно приближается к асимптоте при х+.
Рассмотрим
способ отыскания наклонной асимптоты,
т.е. способ определения чисел k
и
b в уравнении
асимптоты. Разделив равенство (4.8) на х
и перейдя к пределу при х+,
получим
Итак,
(4.9)
Далее,
из соотношения (4.8) получаем:
Таким образом,
(4.10)
Доказано, что если прямая наклонная асимптота, то числа k и b находятся по формулам (4.9) и (4.10). Обратно, если оба предела (4.9) и (4.10) существуют, причём , то прямая является наклонной асимптотой графика функции при х+.
В
самом деле, полагая
и используя равенство (4.10), получаем что
.
Следовательно, справедливо равенство
(4.8):
,
где
,
т.е. прямая
является наклонной асимптотой графика
функции при
.
Практически целесообразно искать асимптоты в следующем порядке: 1) вертикальные асимптоты; 2) горизонтальные асимптоты; 3) наклонные асимптоты.
Пример
1. Найти
асимптоты графика функции
.
Решение.
1) Находим вертикальные асимптоты. Точка
- точка разрыва 2-го рода данной функции,
причем
при
,
при
.
Следовательно, ось ординат (
)
вертикальная асимптота.
2) Находим горизонтальные асимптоты
,
следовательно, горизонтальных асимптот нет.
3) Находим наклонные асимптоты
,
.
Следовательно,
прямая
является наклонной асимптотой графика
данной функции как при
,
так и при
.
График функции схематически изображён на рис. 31.
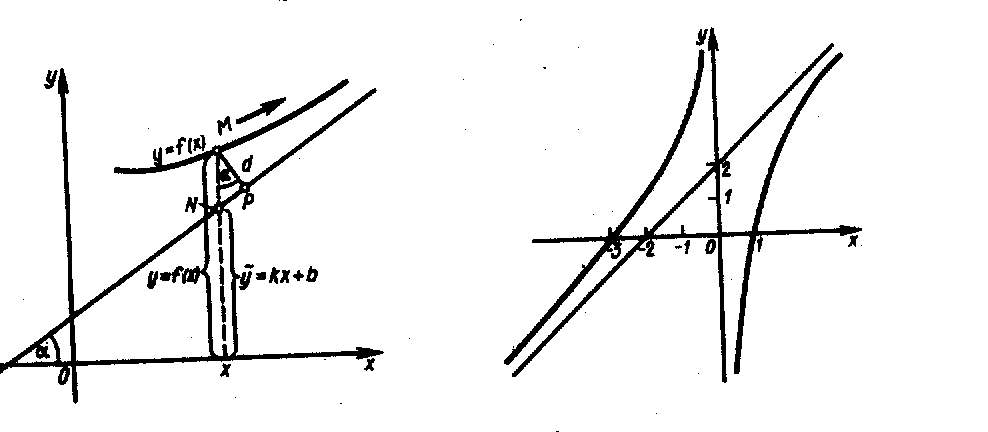
Рис. 30 Рис. 31
Пример
2. Доказать,
что гипербола
имеет своими наклонными асимптотами
прямые
.
Решение.
Так как
,
то
Следовательно,
прямые
являются наклонными асимптотами данной
гиперболы как при
,
так и при
.
5. Схема исследования графика функции. Рассмотрим примерную схему, по которой целесообразно исследовать поведение функции и строить ее график.
1. Найти область определения функции.
2. Найти точки пересечения графика функции с осями координат.
3. Найти асимптоты.
4. Найти точки возможного экстремума.
5. Найти критические точки.
6. С помощью вспомогательного чертежа исследовать знак первой и второй производных. Определить участки возрастания и убывания функции. Найти направление выпуклости графика, точки экстремума и точки перегиба.
7. Построить график, учитывая исследование, проведенное в п. 1 6.
При этом в начале исследования полезно проверить, является данная функция четной или нечетной, чтобы при построении использовать симметрию графика относительно оси ординат или начала координат.
В
качестве примера построим по изложенной
выше схеме график функции
.
1. Областью определения функции является множество всех действительных чисел, кроме , при котором обращается в нуль знаменатель.
2.
Так как уравнение
не имеет действительных корней, то
график функции не имеет точек пересечения
с осью Ox,
но пересекает ось Oy
в точке
.
3.
Выясним вопрос о существовании асимптот.
Исследуем поведение функции вблизи
точки разрыва
.
Так как
при
,
при
,
то прямая
является вертикальной асимптотой
графика функции. Если
(
),
то
(
),
следовательно, горизонтальной асимптоты
у графика нет. Далее, из существования
пределов
вытекает,
что при
и при
график функции имеет наклонную асимптоту
.
4. Для нахождения точек экстремума вычислим первую производную:
Решая
уравнение
,
получаем две точки возможного экстремума:
и
.
Для нахождения критических точек вычислим вторую производную:
Так как в нуль не обращается, то критических точек нет.
Нарисуем
вспомогательный чертеж и исследуем
знак первой и второй производных (рис.
32). Получаем, что функция на (
)
возрастает, на (
)
убывает, а на (
)
снова возрастает.
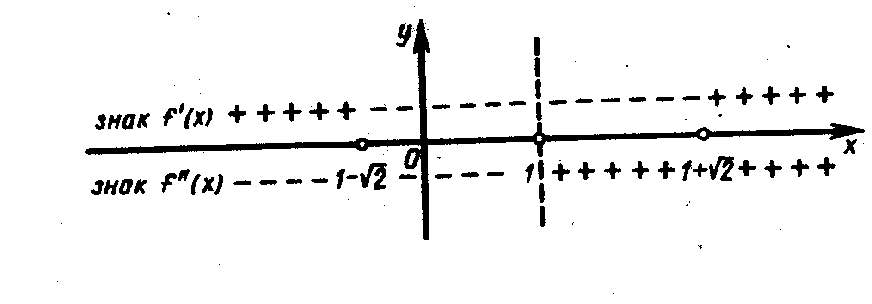Точки экстремума:
1)
максимум при
,
причём
;
2) минимум при
,
причём
.
На (
)
направление выпуклости графика вверх,
а на (
)
- вниз.
Рис. 32
Точки экстремума:
1)
максимум при
,
причём
;
2) минимум при
,
причём
.
На (
)
направление выпуклости графика вверх,
а на (
)
- вниз.
6
.
Используя полученные данные, строим
эскиз графика (рис. 33)