5.5. Частные производные функции нескольких переменных

1. Частные производные функции.

Если в функции нескольких переменных дать определенные численные значения из области задания всем независимым переменным, кроме одной, и предоставить изменяться этой переменной, скажем _, то функция превратится в функцию одной переменной . В частности, рассматривая функцию двух переменных и приписывая аргументу определенное значение , получим функцию одной переменной. Геометрическим образом этой функции является кривая, полученная как пересечение плоскости и поверхности (рис. 49).

Пусть существует производная функции одной переменной в точке _. Это значит, что существует конечный предел отношения приращения функции к приращению аргумента

.

z

z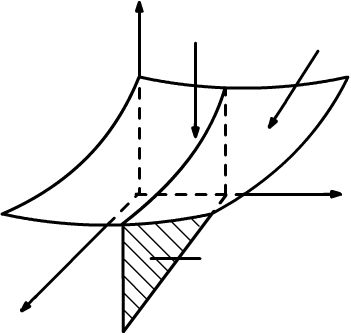

y

x

Рис. 49

Этот предел называется частной производной функции по х в точке и обозначается символом _, или , или , или . (Символ читается как «дэ круглое». Его не следует путать с символом «d»).

Таким образом, частная производная функции по х в точке по определению равна пределу отношения частного приращения функции по х к приращению аргумента , если этот предел существует при :

. (5.11)

Аналогично определяется частная производная функции в точке по переменной у:

. (5.12)

Отметим: из приведенных выше рассуждений следует, что частная производная функции по аргументу представляет собой обыкновенную производную функции одной переменной при фиксированных значениях остальных переменных. Поэтому вычисление частных производных производится по обычным правилам вычисления производных функций одной переменной.

Пример 1. Найти частные производные в точке функции

Решение. Положим , получим функцию, зависящую только от х:

Производная этой функции по х равна : при она равна 142. Таким образом,

.

Для нахождения частной производной функции по у в точке положим . Получаем функцию переменной у:

Отсюда найдем ее производную в точке : .

Следовательно, .

Пример 2. Найти частные производные функции в точке .

Решение. Считая у постоянным, находим производную по х:

_.

При вычислении производной использовалось правило дифференцирования сложной функции одной переменной. Индексы показывают по какой «букве» проводится дифференцирование. Аналогично получим частную производную по у в точке :

_.

Аналогично тому, как определялись частные производные функции двух переменных (формулы (5.11) и (5.12)), определяются частные производные функции большего числа аргументов. Например, для функции трех переменных , частные производные в точке определяются как пределы отношений соответствующих приращений, если эти пределы существуют:

, (5.13)

, (5.14)

. (5.15)

Пример 3. Найти частные производные функции , где

, в точке .

Решение. По правилу дифференцирования сложной функции по х, при постоянных y и z, получим:

Аналогично получим частную производную по у (х и z -постоянные) и по z (x и y - постоянные):

, .