3.4. Правила дифференцирования. Производные основных элементарных функций
1. Правила дифференцирования.
Теорема
1. Если
функции
и
дифференцируемы в точке х,
то сумма, разность, произведение и
частное этих функций (частное
при условии,
что
)
также дифференцируемы в этой точке
и имеют место следующие формулы:
,
,
С л е д с т в и е. Если функции и дифференцируемы в точке х, то
,
,
2. Производная
постоянной функции.
Производная функции
,
где С
– постоянное число, выражается формулой
.
А, в силу теоремы 1, постоянный множитель
можно выносить за знак производной.
3. Производные тригонометрических функций.
1) Производная
функции
выражается формулой
.
2) Производная
функции
выражается формулой
.
3) Производная
функции
выражается формулой
4)
Производная
функции
выражается формулой
4. Производная логарифмической функции.
Производная функции
(
)
выражается формулой
С л е д с т в и е.
Если
,
то
.
5. Производная показательной функции и обратных тригонометрических функций. Пусть функция удовлетворяет условиям теоремы о существовании обратной функции и функция является для нее обратной. Тогда имеет место следующая теорема.
Теорема
2
(о
производной обратной функции).
Если функция
имеет в точке
производную
,
то обратная
функция
также
имеет в
соответству-ющей точке
производную,
причем
(3.5)
Теорема имеет
простой геометрический смысл.
Рассмотрим в некоторой окрестности
точки
график функции
(или обратной функции
.
Пусть точке
на этом графике соответствует точка М
(рис.
12).
Как известно, производная
равна
тангенсу угла
наклона касательной, проходящей через
точку М,
к оси Ох.
Производная обратной функции
равна тангенсу угла
наклона той же касательной к оси Оу.
Поскольку углы
и
в сумме составляют /2,
то формула
(3.5) выражает
очевидный факт:
Рис.
12
Используя сформулированную теорему, продолжим вычисление производных простейших элементарных функций.
1)
Производная функции
(
)
выражается формулой
.
С л е д с т в и е 1.
Если
,
то
.
С л е д с т в и е 2.
Если
,
то
функция
называется
гиперболическим синусом,
а функция
называется
гиперболическим косинусом.
С л е д с т в и е 3.
Если
,
то
.
С л е д с т в и е 4.
Если
,
то
функция
th
x
называется
гиперболическим
тангенсом.
С л е д с т в и е 5.
Если
,
то
функция
cth
x
называется
гиперболическим
котангенсом.
2)
Производная функции
выражается формулой
3)
Производная функции
выражается формулой
4)
Производная
функции
выражается
формулой
5)
Производная
функции
выражается формулой
6. Дифференцирование сложной функции.
Теорема
3. Если
функция
,
имеет производную в точке
,
а функция
имеет производную в соответствующей
точке
,
то сложная
функция
имеет производную в точке
и справедлива
следующая формула:
.
З а м е ч а н и е 1. В данной теореме рассмотрена сложная функция, где у зависит от t через промежуточную переменную х. Возможна и более сложная зависимость с двумя, тремя и большим числом промежуточных переменных, но правило дифференцирования остается таким же.
Так, например, если
,
где
,
a
и
,
то производную
следует вычислять по формуле
.
Пример
1.
Вычислить производную функции
.
Решение.
Данную функцию можно представить в
виде
,
где
.
Тогда по правилу дифференциро-вания
сложной функции
Заменяя и
на
,
окончательно получим
Пример
2.
Вычислить производную функции
Решение.
Данную функцию можно представить в
виде
,
где
,
a
и
.
По правилу дифференцирования сложной
функции
получаем
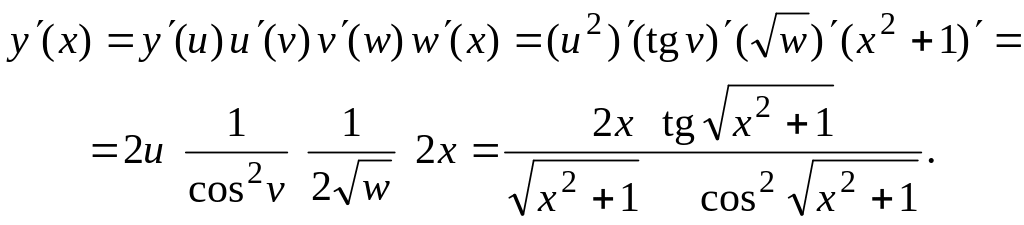
З а м е ч а н и е 2. Иногда производную приходится вычислять непосредственно исходя из ее определения. Найдем, например, производную функции
При производная вычисляется по формулам и правилам дифференцирования:
Этим выражением нельзя воспользоваться при . В точке производную можно вычислить, используя определение производной:
т.к. произведение бесконечно малой функции на ограниченную есть бесконечно малая. Таким образом,
Теорема 4 (инвариантность формы дифференциала). Дифференциал функции у выражается по одной и той же формуле независимо от того, будет ли у рассматриваться как функция от независимой переменной х, или от зависимой переменной х.
7.
Логарифмическая производная. Производная
степенной функции. Вычислим
производную функции
(
).
Так как
и
(последнее равенство получено на
основании правила дифференцирования
сложной функции),
то
производная
данной функции выражается следующей
формулой
Учитывая эту
формулу,
вычислим производную сложной функции
,
где
дифференцируемая функция. Имеем
или
Производная
называется логарифмической
производной
функции
.
Для упрощения записи при логарифмическом
дифференцировании знак модуля у функции
обычно опускается.
Вычислим с помощью
логарифмической производной производную
показательно-степенной функции
,
где и
и v
–
некоторые
функции от х
(
),
имеющие в данной точке х
производные
и
.
Так как
,
то имеем
Отсюда, учитывая, что , получаем следующую формулу для производной показательно-степенной функции:
Пример.
Вычислить производную функции
.
Решение.
Данную функцию можно представить в
виде
,
где
и
.
Поэтому
Логарифмическая производная очень удобна при нахождении производной степенной функции с любым вещественным показателем.
Производная
степенной функции с любым действительным
показателем
(
любое вещественное число) выражается
формулой
8. Таблица производных простейших элементарных функций. Нами вычислены производные всех простейших элементарных функций и мы можем составить следующую таблицу производных.
I. (С) = 0.
II.
в частности
III.
(logа
х)
=
logа
е, в частности (ln
х)
=
.
IV.
в частности,
V. (sin х) = cos х.
VI. (cos х) = sin х.
vii.
(tg x)
=
VIII.
(ctg x)=
IX.
(arcsin х)
=
.
X.
(arccos x)
=
.
XI.
(arctg
x)
=
.
XII.
(arcctg x)
=
.
XIII. (sh х) = ch х.
XIV. (ch х) = sh х.
XV.
(th
x)
=
XVI.
(cth
x)
=
Формулы, приведенные в таблице, а также правила дифференцирования суммы, разности, произведения, частного и правило дифференцирования сложной функции являются основными формулами дифференциального исчисления. На основе правил и формул дифференцирования можно сделать важный вывод: производная любой элементарной функции также элементарная функция. Таким образом, операция дифференцирования не выводит из класса элементарных функций.