2. Механический смысл и геометрическое истолкование.
Рассмотрим механический смысл частной производной.
В ряде разделов
механики, физики и технических дисциплин
читатель встречался с функциями
нескольких переменных, одной из которых
являлась временная переменная t.
Например, изучая движение материальной
системы, имеющей n
степеней свободы, в теоретической
механике в качестве характеристических
функций, описывающих динамику системы,
рассматриваются функции Лагранжа
или Гамильтона
,
где
- обобщенные координаты,
-
обобщенные скорости,
-
обобщенные импульсы,
и V
– кинетическая и потенциальная энергия
системы. В этом случае, как известно из
теоретической механики, уравнение
движения механической системы содержит
частную производную по времени
.
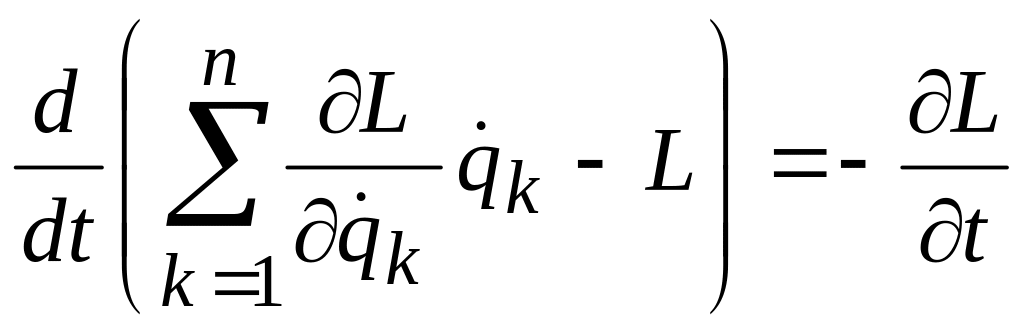Другой пример
знаком нам из теплотехники. Пусть в
начальный момент времени
задано распределение температуры тела
и задан тепловой режим на его границах.
Тогда при
температура тела в точке
будет являться функцией времени
.
Вид координатной и временной зависимости
температуры тела определяется типом
теплового режима на границах и
дифференциальным уравнением
теплопроводности, содержащим частную
производную по времени
.
Таким образом,
уравнения, описывающие механическое
движение системы и распределение
температуры в теле, содержат величины,
характеризующие их изменение во времени.
Каждая из величин в правых частях
уравнений является пределом при
соответствующих отношений
или
Каждое выражение
представляет собой изменение
соответствующей функции, отнесенное к
промежутку времени, в течение которого
эти изменения произошли. То есть среднюю
скорость изменения величины за время
.
В пределе, при
,
мы получаем мгновенную скорость изменения
функции Лагранжа или температуры. В
этом заключается механический смысл
частной производной некоторой функции
по времени.
По аналогии с этим,
частные производные
функции
по переменной
также трактуются как скорость изменения
функции
в точке М
в направлении оси
.
Перейдем
к выяснению геометрического
смысла частных
производных функции
двух переменных
.
Как мы знаем из п.4.2, графиком такой
функции является некоторая поверхность
в трехмерном пространстве. Фиксируя
аргумент
,
мы получим плоскую кривую
,
представляющую собой сечение поверхности
плоскостью, параллельной координатной
плоскости
.
Пусть
-
касательная
к кривой
в точке
,
,
-
угол, образованный этой касательной с
положительным направлением оси
.
Поскольку по определению частной производной
,
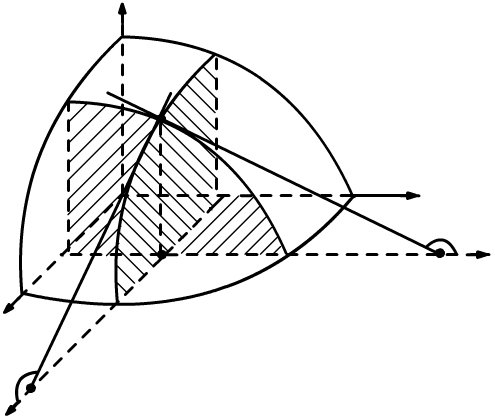
то на основании геометрического смысла производной функции одной переменной, заключаем (рис. 50)
.
z
y
B
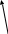
x
A
lx
Рис. 50
Аналогично, если
есть сечение поверхности
плоскостью
,
- угол, образованный с осью
касательной
к кривой
в точке
,
то
.
3. Дополнительный материал.
В отличие от функций одной переменной, из существования частных производных в некоторой точке, вообще говоря, не вытекает непрерывность функции многих переменных в этой точке. Рассмотрим, например, функцию
Мы убедились (см.п.5.4), что эта функция не является непрерывной в точке . Однако эта функция всюду (включая точку ) имеет частные производные. Действительно, имеем в точке :
В остальных точках плоскости существование производных очевидно.
Но если частные производные существуют и ограничены, то функция будет непрерывной. Это свойство выражается следующим утверждением.
Теорема. Если функция имеет частные производные по х и по у всюду в области D и эти производные всюду удовлетворяют неравенствам
,
,
где М - постоянная, то функция непрерывна в области D.
Замечание.Данное выше понятие частных производных - формулы (5.11) и (5.12), пригодно для внутренних точек области. Но для граничных точек этой области, вообще говоря, непригодно. Это связано с тем, что в граничных точках области задания функции (рис.51) не всегда можно вычислить частные приращения функции. В связи с этим принято определять частные производные функций в граничных точках области определения как пределы производных при стремлении точек к границе.
y
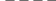
x
Рис. 51