
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко математический анализ
- •Часть 1
- •Учебное пособие
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко
- •Часть 1
- •Введение
- •1. Предел последовательности
- •1.1. Множество действительных чисел
- •1.2. Числовые последовательности
- •2. Ограниченные и неограниченные последовательности.
- •1.3. Сходящиеся последовательности
- •1. Понятие сходящейся последовательности.
- •З а м е ч а н и е. Неравенство (1.1) равносильно неравенствам
- •2. Основные свойства сходящихся последовательностей.
- •, Где есть бесконечно малая.
- •1.4. Монотонные последовательности
- •1. Определение и признак сходимости монотонных последовательностей.
- •Задачи к п. 1
- •Ответы к п. 1
- •2. Функции одной переменной
- •2.1. Классификация функций
- •2.2. Предел функции
- •2.3. Теоремы о пределах функции
- •2.4. Два замечательных предела
- •1. Первый замечательный предел .
- •2. Второй замечательный предел
- •2.5. Бесконечно малые и бесконечно большие функции
- •1. Бесконечно малые функции.
- •2. Бесконечно большие функции.
- •2.6. Сравнение бесконечно малых и бесконечно больших функций
- •2.7. Непрерывные функции
- •2.8. Классификация точек разрыва
- •1. Определение и классификация точек разрыва функции.
- •2.9. Основные свойства непрерывных функций
- •Задачи к п. 2
- •Ответы к п. 2
- •3. Дифференцирование
- •3.1. Производная функции
- •4. Правая и левая производные.
- •3.2. Дифференцируемость функции
- •1. Понятие дифференцируемости функции в данной точке.
- •2. Связь между понятиями дифференцируемости и непрерывности.
- •3.3. Дифференциал функции
- •3.4. Правила дифференцирования. Производные основных элементарных функций
- •1. Правила дифференцирования.
- •3. Производные тригонометрических функций.
- •4. Производная логарифмической функции.
- •6. Дифференцирование сложной функции.
- •3.5. Производные и дифференциалы высших порядков
- •2. Формулы для n-х производных некоторых функций.
- •4. Дифференциалы высших порядков.
- •3.6. Параметрическое задание функции и ее дифференцирование
- •Задачи к п. 3
- •Ответы к п. 3
- •4. Применение дифференциального исчисления к исследованию функций
- •4.1. Основные теоремы дифференциального исчисления
- •4.2. Раскрытие неопределенностей. Правило Лопиталя
- •4.3. Формула Тейлора
- •Формула Тейлора.
- •3. Разложение некоторых элементарных функций по формуле Маклорена.
- •4.4. Исследование поведения функций и построение графиков
- •1. Признак монотонности функции.
- •2. Отыскание точек локального экстремума функции.
- •Задачи к п. 4
- •Ответы к п. 4.
- •5. Функции нескольких переменных Введение
- •5.1. Предварительные сведения: n – мерное координатное и n – мерное евклидово пространства
- •Координатное и евклидово пространства.
- •2. Множества точек n – мерного евклидова пространства.
- •5.2. Понятие функции многих переменных
- •1. Механическая модель функциональной зависимости.
- •2. Функция и область ее задания.
- •3. Геометрическое изображение функций.
- •5.3. Предел функции нескольких переменных
- •1. Предел последовательности точек.
- •2. Предел функции.
- •3. Бесконечно малые функции.
- •5.4. Непрерывность функции нескольких переменных
- •1. Непрерывность функции в точке и на множестве.
- •2. Свойства непрерывных функций нескольких переменных.
- •3. Дополнение о разрывах непрерывности.
- •5.5. Частные производные функции нескольких переменных
- •1. Частные производные функции.
- •2. Механический смысл и геометрическое истолкование.
- •3. Дополнительный материал.
- •5.6. Производные сложных функций. Производная по направлению и градиент. Экстремумы функции двух переменных
- •1. Производные сложных функций.
- •2. Производная по направлению. Градиент.
- •Ответ на вопрос о том, при каких условиях значения смешанных производных не зависят от того, в каком порядке производится дифференцирование, дает следующая теорема.
- •4. Экстремумы функции двух переменных.
- •5. Условный экстремум функции нескольких переменных.
- •Задачи к п. 5.
- •Ответы к п. 4
- •Библиографический список
- •Оглавление
- •1. Предел последовательности …..……………..…………4
- •2. Функции одной переменной ...……………………......18
- •3. Дифференцирование ……..……………………………...46
- •4. Применение дифференциального исчисления к
- •5. Функции нескольких переменных….……....………..111
- •Бырдин Аркадий Петрович
- •Часть 1
- •394026 Воронеж, Московский просп., 14
Задачи к п. 3
Найти производные следующих функций:
1.
![]() 2.
2.
![]() 3.
3.
![]()
4.
![]() 5.
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]() 9.
9.
![]()
10.
![]() 11.
11.
![]() 12.
12.
![]() 13.
13.
![]() 14.
14.
![]() 15.
15.
![]()
16.
![]() .
17.
.
17.
![]() 18.
18.
![]() 19.
19.
![]() 20.
20.
![]() 21.
21.
![]() 22.
22.
![]()
Используя предварительное логарифмирование, найти производные следующих функций:
23.
![]() 24.
24.
![]() 25.
25.
![]() 26.
26.
![]() 27.
27.
![]() 28.
28.
![]()
Для функций,
заданных параметрически, найти
![]()
29.
![]()
30.
![]()
31.
![]() .
.
32.
![]()
Найти производные второго порядка следующих функций:
33.
![]() 34.
34.
![]() 35.
35.
![]() 36.
36.
![]()
Найти производные второго порядка следующих функций заданных параметрически:
37.
![]()
38.
![]()
Написать уравнение
касательной и нормали к графику функций
![]() в данной точке, если:
в данной точке, если:
39.
![]()
40.
![]()
41.
![]()
42.
![]()
43.
В какой точке
![]() кривой
кривой
![]() касательная перпендикулярна к прямой
касательная перпендикулярна к прямой
![]()
44.
Составить уравнение нормали к параболе
![]() в точке пересечения с биссектрисой
первого координатного угла.
в точке пересечения с биссектрисой
первого координатного угла.
45.
Закон движения материальной точки по
прямой имеет вид
![]()
а) В какие моменты времени точка находится в начале координат?
б) В какие моменты времени направление ее движения совпадает с положительным направлением оси Ох?
в) В какие моменты времени ее ускорение равно нулю?
46.
Тело массой 4 движется прямолинейно по
закону
![]() Определить кинетическую энергию тела
в момент времени t
= 5.
Определить кинетическую энергию тела
в момент времени t
= 5.
47. Радиус шара изменяется со скоростью v. С какой скоростью изменяются объем и площадь поверхности шара?
48.
Доказать, что для линейной функции
![]() приращение
и дифференциал dy
совпадают.
приращение
и дифференциал dy
совпадают.
49.
Найти приращение
и дифференциал dy
функции
![]() соответствующие значению аргумента
соответствующие значению аргумента
![]() и двум различным значениям аргумента
и двум различным значениям аргумента
![]()
50.
Найти приращение
![]() и дифференциал dS
площади S
квадрата, соответствующие приращению
стороны x.
С помощью рисунка геометрически
истолковать
и дифференциал dS
площади S
квадрата, соответствующие приращению
стороны x.
С помощью рисунка геометрически
истолковать
![]() и разность
и разность
![]() .
.
Найти дифференциал
указанных функций при произвольных
значениях аргумента х
и при
произвольном его приращении
![]()
51.
![]() 52.
52.
![]()
53.
![]() 54.
54.
![]()
55.
Вычислить приближенно: а)
![]() б)
б)
![]() в)
в)
![]()
56.
Обосновать приближенную формулу
![]() и вычислить по этой формуле
и вычислить по этой формуле
![]()
57.
Найти приближенное значение функции
![]() при
при
![]() .
.
Ответы к п. 3
39. 7x
+ y
3 = 0, x
7y
+ 71 = 0. 40.
y
5 = 0, x
+ 2 = 0. 41.
x
4y
+ 4 = 0, 4x
+
y
18
= 0. 42.
y
2x
= 0, x
+
2y
= 0. 43.
![]() 44.
44.
![]() .
45. а)
.
45. а)![]() б)
б)
![]() в)
в)
![]() 46. 242.
47.
46. 242.
47.
![]() 49.
49.
![]()
![]() 50.
50.
![]() 55. а)
0.05;
б) 0.805;
в) 0.2.
56. 2.93.
57. 1.2.
55. а)
0.05;
б) 0.805;
в) 0.2.
56. 2.93.
57. 1.2.
4. Применение дифференциального исчисления к исследованию функций
4.1. Основные теоремы дифференциального исчисления
Теорема
1 (теорема
Ферма).
Пусть функция
определена на интервале
![]() и в некоторой
точке
и в некоторой
точке
![]() этого интервала имеет наибольшее или
наименьшее значение.
Тогда, если в точке
существует производная, то она равна
нулю, т.
е.
этого интервала имеет наибольшее или
наименьшее значение.
Тогда, если в точке
существует производная, то она равна
нулю, т.
е.
![]()
Геометрический
смысл теоремы Ферма состоит в том, что
если в точке
дифференцируемая
функция
имеет
наибольшее или наименьшее значение, то
в точке
![]() касательная к графику функции
параллельна оси Ox
(рис. 13).
касательная к графику функции
параллельна оси Ox
(рис. 13).
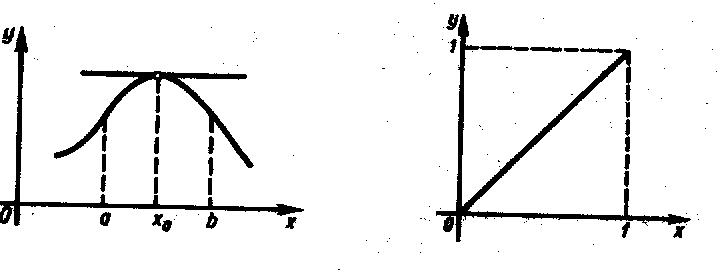
Рис. 13 Рис. 14
З
а м е ч а н и е. Теорема неверна, если
функцию
рассматривать на отрезке
.
Так функция
на отрезке
[0,1] в точке
принимает наименьшее, а в точке
![]() – наибольшее значение, однако как в
той, так и в другой точке производная
в нуль не обращается, а равна единице
(рис. 14).
– наибольшее значение, однако как в
той, так и в другой точке производная
в нуль не обращается, а равна единице
(рис. 14).
Теорема
2 (теорема
Ролля).
Пусть на
определена
функция
,
причем:
1)
непрерывна на
;
2)
дифференцируема на
;
3)
![]() .
Тогда существует точка
.
Тогда существует точка
![]() ,
в которой
,
в которой
![]() .
.
Г еометрически
теорема Ролля означает, что у графика
непрерывной на отрезке
и дифференцируемой внутри этого отрезка
функции, принимающей на его концах
равные значения, существует точка
еометрически
теорема Ролля означает, что у графика
непрерывной на отрезке
и дифференцируемой внутри этого отрезка
функции, принимающей на его концах
равные значения, существует точка
![]() ,
в которой
касательная параллельна оси Ох
(рис. 15). На рис. 15 в точке с
функция
принимает наибольшее значение.
,
в которой
касательная параллельна оси Ох
(рис. 15). На рис. 15 в точке с
функция
принимает наибольшее значение.
Рис. 15
Следует отметить, что все три условия теоремы Ролля существенны. Чтобы убедиться в этом, достаточно привести примеры функций, для которых выполнялись бы два условия теоремы, а третье не выполнялось и производные которых не
Рис. 3![]() ,
и равная 0, если
(рис. 16), удовлетворяет условиям 2
и 3,
но не удовлетворяет условию 1.
Функция
,
и равная 0, если
(рис. 16), удовлетворяет условиям 2
и 3,
но не удовлетворяет условию 1.
Функция
![]() ,
x[1,1]
(рис. 17) удовлетворяет условиям 1
и 3,
но не удовлетворяет условию 2.
Для этих функций также не существует
точки, в которой их производная обращалась
бы в нуль.
,
x[1,1]
(рис. 17) удовлетворяет условиям 1
и 3,
но не удовлетворяет условию 2.
Для этих функций также не существует
точки, в которой их производная обращалась
бы в нуль.
 Рис.
16
Рис. 17
Рис.
16
Рис. 17
Отметим, что в математике существенность тех или иных условий доказываемых теорем проверяется построением соответствующих примеров, когда невыполнение того или иного условия теоремы приводит к тому, что утверждение теоремы становится неверным.
Теорема
3 (теорема
Лагранжа).
Пусть на
определена
функция
,
причем:
1)
непрерывна на
;
2)
дифференцируема на
.
Тогда
существует точка
![]() такая, что справедлива формула
такая, что справедлива формула
![]()
Установим
геометрический смысл теоремы Лагранжа
(рис.18). Величина
![]() является угловым коэффициентом секущей,
проходящей через точки
является угловым коэффициентом секущей,
проходящей через точки
![]() и
и
![]() графика функции
графика функции
![]() а
а
![]()
угловой коэффициент касательной к
графику в точке
угловой коэффициент касательной к
графику в точке
![]() Из теоремы Лагранжа следует, что
существует точка с
такая, что
касательная к графику в точке
Из теоремы Лагранжа следует, что
существует точка с
такая, что
касательная к графику в точке
![]() параллельна секущей
параллельна секущей
![]() Таких точек может быть и несколько, но,
по крайней мере, одна всегда существует.
Таких точек может быть и несколько, но,
по крайней мере, одна всегда существует.

З а м е ч а н и е 1. Равенство
Рис. 74![]()
называется формулой Лагранжа или формулой конечных приращений.
З
а м е ч а н и е 2. Так как точка
с лежит
между a
и b,
то
![]() ,
где
,
где
![]() .
Учитывая это, формулу Лагранжа можно
записать в виде
.
Учитывая это, формулу Лагранжа можно
записать в виде
![]()
З
а м е ч а н и е 3. Если положить
![]() то получим
то получим
![]() Такая запись формулы Лагранжа часто
бывает удобнее, чем запись в виде (4.1).
Такая запись формулы Лагранжа часто
бывает удобнее, чем запись в виде (4.1).
Как будет показано в дальнейшем, теорема Лагранжа лежит в основе доказательства многих формул и теорем анализа.
Теорема
4 (теорема
Коши).
Пусть функции
и
непрерывны на
и дифференцируемы
на
.
Пусть,
кроме того,
![]() .
Тогда
существует точка
такая, что справедлива формула
.
Тогда
существует точка
такая, что справедлива формула
![]() .
(4.2)
.
(4.2)
З а м е ч а н и е. Формула (4.2) называется формулой Коши или обобщенной формулой конечных приращений.
