4. Правая и левая производные.

Определение. Правой (левой) производной функции в точке называется правый (левый) предел отношения при (при условии, что этот предел существует).

Обозначение:

.

Если функция имеет в точке производную, то она имеет в этой точке правую и левую производные, которые совпадают. Вместе с тем существуют функции, имеющие в данной точке правую и левую производные, но не имеющие производной в этой точке. Это, например, функция , которая имеет в точке правую производную, рав­ную (при ), и левую производную, равную (при ), но не имеет в этой точке производной, так как

7. 3.2. Дифференцируемость функции

8. 1. Понятие дифференцируемости функции в данной точке.

Определение. Функция называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде

, (3.1)

где А  некоторое число, не зависящее от , a –

функция аргумента , являющаяся бесконечно малой при

, т. е.

Установим связь между дифференцируемостью функции в точке и существованием производной в той же точке.

Теорема 1. Для того чтобы функция была диф­ференцируема в точке , необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Таким образом, для функций одной переменной дифференцируемость и существование производной  понятия равносильные. Поэтому операцию нахождения производной часто называют дифференцированием.

2. Связь между понятиями дифференцируемости и непрерывности.

Теорема 2. Если функция дифференцируема в данной точке , то она и непрерывна в этой точке.

З а м е ч а н и е. Обратное утверждение неверно. Функция может быть непрерывной в точке, но не быть дифференцируемой, т.е. не иметь производной в этой точке. Примером такой функции служит функция , ко­торая непрерывна в точке , но не имеет в этой точке производной, т.е. не является дифференцируемой.

Если функция имеет производную в каждой точке неко­торого промежутка (дифференцируема в каждой точке этого про­межутка), то будем говорить, что функция дифференцируема на указанном промежутке.

3.3. Дифференциал функции

1. Определение и геометрический смысл дифференциала. Пусть функция дифференцируема в точке , т.е. ее прираще­ние у в этой точке можно записать в виде суммы двух слагаемых:

, где

Слагаемое является при бесконечно малой одного порядка с (при А  0), оно линейно относительно . Слагаемое при – бесконечно малая более высокого порядка, чем .

Таким образом, первое слагаемое (при А  0) является глав­ной частью приращения функции .

Определение. Дифференциалом функции в точке называется главная, линейная относительно , часть прира­щения функции в этой точке:

. (3.2)

Если , то , и поэтому слагаемое уже не является главной частью приращения у, так как слагаемое , вообще говоря, отлично от нуля. Однако и в этом слу­чае по определению полагаем дифференциал функции в точке равным , т.е. .

Учитывая, что , формулу (3.2) можно записать в виде

. (3.3)

Пусть . Тогда по формуле (3.3)

Поэтому дифференциалом независимой переменной х назовем приращение этой переменной . Соотношение (3.3) принимает теперь вид

. (3.4)

З

Рис. 51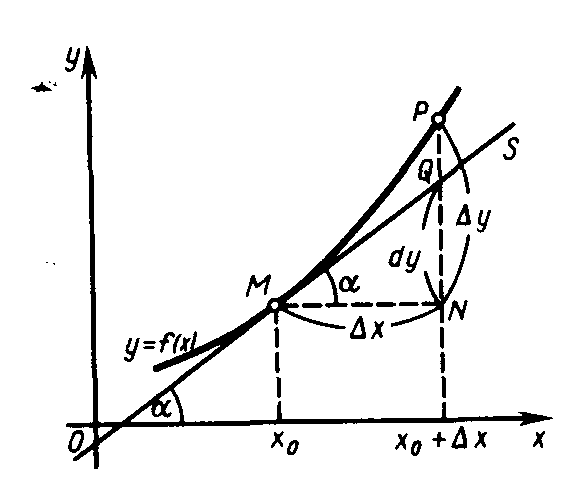

аметим, что с помощью равенства (3.4) производную можно вычислить как отношение дифференциала функции к дифференциалу независимой переменной, т. е.

Рис. 11

Дифференциал функции имеет следующий геометрический смысл. Пусть точка М на графике функции соответствует значению аргумента , точка Р  значению аргумента , прямая MS  касательная к графику в точке М,   угол между касательной и осью Ох. Пусть, далее MN || Ox, PN || Оу , Q  точка пересечения касательной MS с прямой PN (рис. 11). Тогда приращение функции равно величине отрезка NP. В то же время из прямоугольного треугольника MNQ получаем: , т.е. дифференциал функции равен величине отрезка NQ. Из геометрического рассмотрения видно, что величины отрезков NP и NQ различны. Таким образом, дифференциал функции в точке равен приращению «ординаты касательной» к графику этой функции в точке , а приращение функции y есть приращение «ординаты самой функции» в точке , соответствующее приращению аргумента, равному .

2. Приближенные вычисления с помощью дифференциала. Из определения дифференциала следует, что он зависит линейно от и является главной частью приращения функции y. Само же y зависит от более сложно. Во многих задачах приращение функции в данной точке приближенно заменяют дифференциалом функции в этой точке: .

Пример. Покажем, что если  мало, то можно использовать приближенную формулу

Решение. Рассмотрим функцию При малых х имеем

откуда, положив , х = , получим

В частности, при  = 0.0003.