3.3. Метод Зейделя

Метод Зейделя представляет собой модификацию метода итераций. Основная его идея заключается в том, что при вычислении -го приближения неизвестной учитываются уже вычисленные ранее -е приближения неизвестных .

Запишем систему (3.6) в виде

Выберем произвольно начальные приближения корней . Тогда первое приближение по методу Зейделя вычисляется по формулам

Так же вычисляются следующие приближения

Обычно метод Зейделя дает лучшую сходимость, чем метод простой итерации. Процесс Зейделя может сходиться даже в том случае, если расходиться процесс итерации. Однако, возможны случаи, когда процесс Зейделя сходится медленнее процесса итерации или, когда процесс итерации сходится, а процесс Зейделя расходится.

Пример. Методом Зейделя решить систему уравнений

Решение. Приведем эту систему к виду, удобному для итерации,

В качестве нулевых приближений корней возьмем

Применяя процесс Зейделя, последовательно получим

Результаты вычислений с точностью до четырех знаков помещены в таблице 4.

Таблица 4

0 1 2 3 4 5	1.2000 1.2000 0.9992 0.9996 1.0000 1.0000	0.0000 1.0600 1.0054 1.0001 1.0000 1.0000	0.0000 0.9480 0.9991 1.0001 1.0000 1.0000

Точные значения корней: .

4. Методы численного решения

НЕЛИНЕЙНЫХ УРАВНЕНИЙ

4.1. Отделение корней

При решении многих алгебраических и трансцендентных уравнений точное значение их корней определить бывает достаточно сложно. Поэтому важное значение приобретают способы приближенного нахождения корней и оценки степени их точности.

Пусть дано уравнение

, (4.1)

где - непрерывная функция от . Всякое значение , обращающее функцию в нуль, т.е. такое, что , называется корнем уравнения (4.1) или нулем функции .

Приближенное нахождение действительных корней уравнения обычно складывается из двух этапов:

1. отделение корней, т.е. установление промежутков, в которых содержится только один корень уравнения;

2. уточнение приближенных корней, т.е. доведение их до заданной степени точности.

Известно, что если функция непрерывна и принимает на концах отрезка значения разных знаков, т.е. , то внутри этого промежутка имеется хотя бы один корень уравнения. Отделение корней уравнения для непрерывной в области определения функции можно осуществить различными способами.

1. Составляют таблицу значений функции на определенном промежутке изменения аргумента , и если окажется, что для соседних значений аргументов значения функции имеют разные знаки, то корень находится между ними.

2. Уравнение заменяют равносильным . Строят графики функций и ; искомый корень является абсциссой точки пересечения этих графиков.

3. Строят график функции на промежутке изменения ; тогда абсцисса точки пересечения графика с осью - корень уравнения, т.е. .

Пример. Выяснить, сколько корней имеет уравнение , и найти промежутки, в которых находятся эти корни.

Решение. Рассмотрим три функции:

.

Уравнение эквивалентно уравнению . Отелим его корни двумя способами (таблица 5).

Таблица 5

-3.0 -2.0 -1.0 0.0 1.0	-14.05 -4.14 1.63 3.00 -0.72	-14.00 -4.00 2.00 4.00 2.00	0.05 0.14 0.37 1.00 2.72

1. Из таблицы значений функции на промежутке с шагом изменения , равным 1, видно, что существуют корни на отрезках и , так как значения функции на концах отрезка имеют разные знаки.

2. Графики функций и пересекаются в двух точках, абсциссы которых являются решениями уравнения , заключенными в указанных промежутках (рис.1).

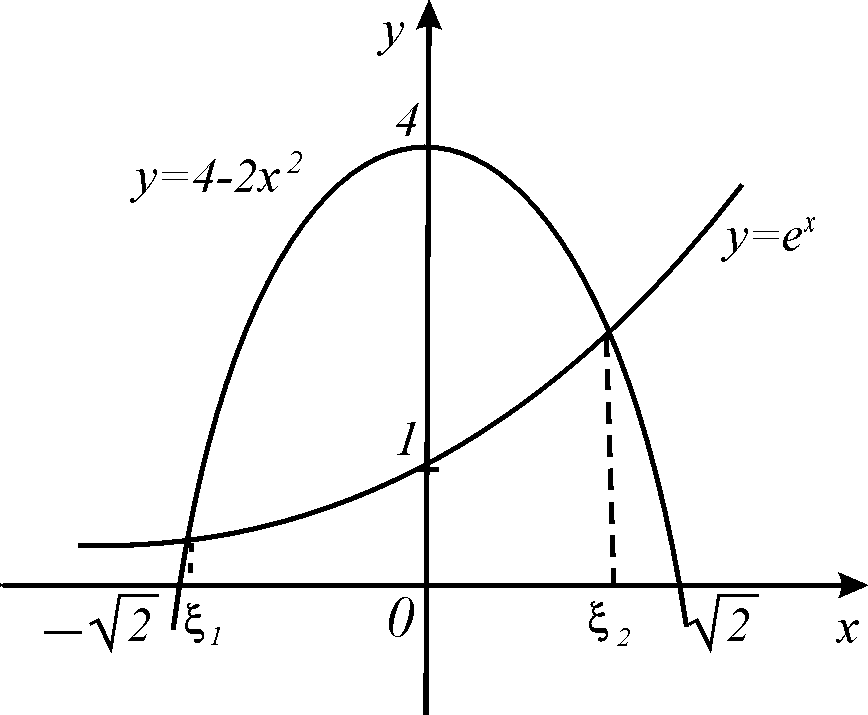
Рис.1

После отделения корней производится итерационное уточнения каждого корня одним из существующих методов. Рассмотрим простейшие методы уточнения корней.