8. Численное решение обыкновенных дифференциальных уравнений

8.1. Понятие о численном решении задачи Коши

Дифференциальное уравнение первого порядка, разрешенное относительно производной, имеет вид

(8.1)

Решением дифференциального уравнения (8.1) называется функция , подстановка которой в уравнение обращает его в тождество. График решения называется интегральной кривой. Задача Коши для дифференциального уравнения (8.1) состоит в том, чтобы найти решение этого уравнения, удовлетворяющее начальному условию

. (8.2)

Пару чисел ( называют начальными данными. Решение задачи Коши называется частным решением уравнения (8.1) при условии (8.2).

Частному решению соответствует одна из интегральных кривых, проходящих через точку ( .

Условия существования и единственности решения задачи Коши содержатся в следующей теореме.

Теорема. Пусть функция - правая часть дифференциального уравнения (8.1) – непрерывна вместе со своей частной производной по переменной в некоторой области на плоскости. Тогда при любых начальных данных ( задача Коши (8.1) - (8.2) имеет единственное решение .

При выполнении условий теоремы Коши через точку на плоскости проходит единственная интегральная кривая.

Численное решение задачи Коши (8.1) - (8.2) состоит в том, чтобы получить искомое решение в виде таблицы его приближенных значений для заданных значений аргумента на некотором отрезке :

(8.3)

Точки (8.3) называют узловыми точками, а множество этих точек называют сеткой на отрезке . Будем использовать равномерную сетку с шагом : .

Приближенные значения численного решения задачи Коши в узловых точках обозначим через ; таким образом,

Для любого численного метода решения задачи (8.1) -(8.2) начальное условие (8.2) выполняется точно, т.е. .

Величина погрешности численного метода решения задачи Коши на сетке отрезка оценивается величиной

,

т.е. расстоянием между векторами приближенного решения ( и точного ( .

Рассмотрим некоторые методы решения задачи Коши.

0. 8.2. Метод Эйлера

Простейшим численным методом решения задачи Коши (8.1) - (8.2) является метод Эйлера, называемый иногда методом ломаных Эйлера.

Угловой коэффициент касательной к интегральной кривой в точке есть .

Найдем ординату касательной, соответствующей абсциссе . Так как уравнение касательной к кривой в точке имеет вид , то . Угловой коэффициент в точке также находится из данного дифференциального уравнения . На следующем шаге получаем новую точку , причем , . Продолжая вычисления в соответствии с намеченной схемой, получим формулы Эйлера для приближенных значений решения задачи Коши с начальными данными ( на сетке отрезка с шагом :

(8.4)

Геометрический смысл метода Эйлера заключается в том, что интегральная кривая на каждом отрезке , , …, заменяется отрезком касательной к интегральной кривой, проходящей через точки , а интегральная кривая заменяется ломаной, проходящей через точки , , …, . Эта ломаная называется ломаной Эйлера (рис.14).

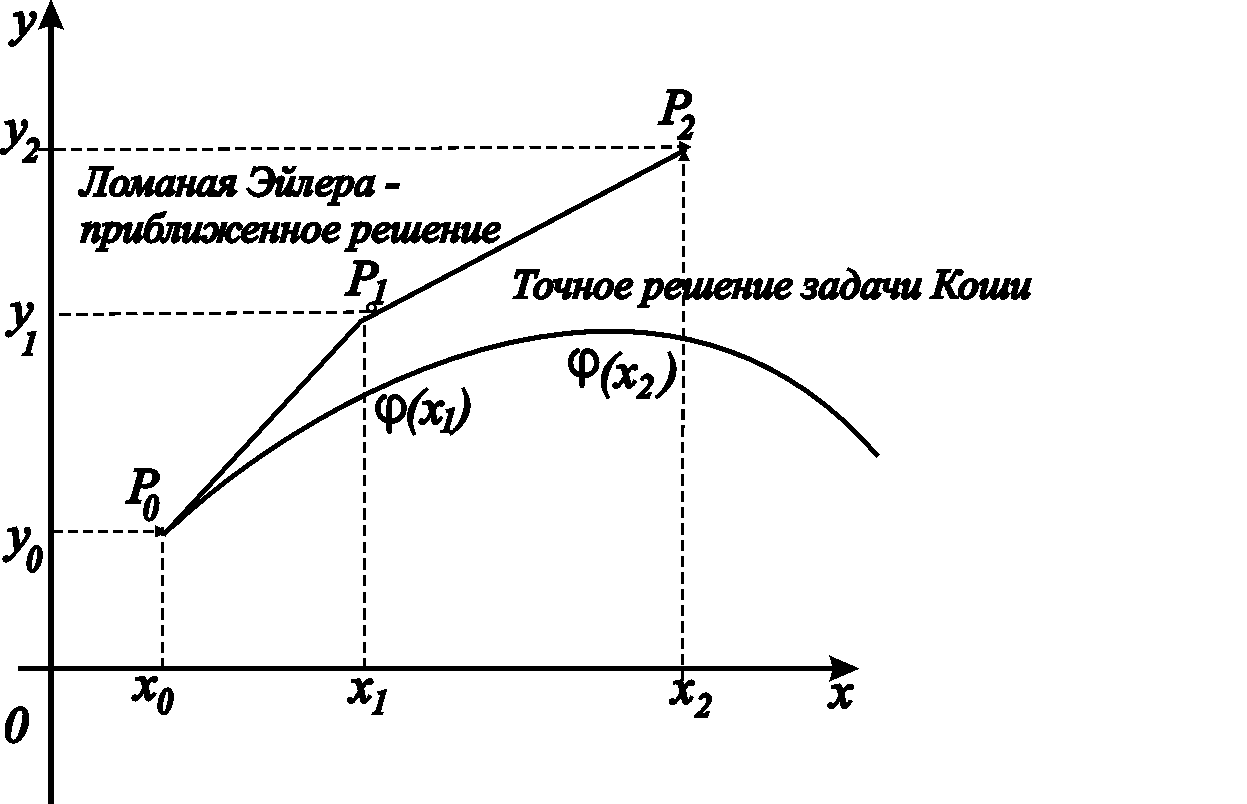
Рис.14

Для оценки погрешности метода Эйлера на одном шаге запишем разложение точного решения задачи Коши в точке по формуле Тейлора с остаточным членом в форме Лагранжа:

Погрешность метода на одном шаге имеет порядок , так как .

После шагов погрешность вычисления значения в конечной точке отрезка возрастает не более чем в раз.

Пример. Найти решение задачи Коши , методом Эйлера на отрезке , с шагом . Сравнить полученные результаты с точным значением. Аналитическое решение задачи имеет вид

Решение. Здесь

Используя рекуррентные формулы

последовательно находим

при

при

при

при

Обозначим и представим результаты вычислений в таблице 9.

Таблица 9

1	0.1	1.1	1.110342	0.005342
2	0.2	1.22	1.242805	0.011793
3	0.3	1.362	1.399718	0.019572
4	0.4	1.5282	1.583649	0.028738