Интерполяционный многочлен Ньютона
Рассмотрим случай, когда узлы интерполяции делят
отрезок
на
равных частей длиной
.
Числа
...,
называют первыми разностями функции , или разностями первого порядка. По ним можно составить разности второго порядка, или вторые разности
...,
и вообще разности любого порядка , или -е разности
.
(2.10)
Табличные разности различных порядков удобно располагать в форме таблиц двух видов: горизонтальной таблицы разностей (таблица 1) или диагональной таблицы разностей (таблица 2).
Равенства (2.10) определяют разности
различных порядков последовательно.
Можно выразить конечные разности любого
порядка, непосредственно через значения
функции в узловых точках. Действительно,
так как
и
то
.
Точно так же
.
Продолжая вычисления, можно убедиться,
что верно равенство
.
(2.11)
Горизонтальная таблица разностей. Таблица 1
|
|
|
|
|
|
|
|
|
|
|
|
Диагональная таблица разностей. Таблица 2
Эта формула
имеет место и для разности
;
достаточно ко всем номерам значений
функции прибавить
.
Формула (2.11) легко запоминается, если
заметить, что ее выражение напоминает
разложение
по формуле бинома Ньютона. Надо только
вместо
писать
,
вместо
писать
и т.д.; в последнем слагаемом вместо
пишем
.
Будем искать интерполяционный многочлен Ньютона в виде
(2.12)
Коэффициенты
определим из условий
Для этого сначала подставим в (2.12) вместо
значение
.
Тогда
.
Далее, пологая
,
получаем
,
или, так как
,
,
откуда
.
Продолжая
вычисление коэффициентов, положим
.
Тогда
.
Заменим найденные коэффициенты , их значениями
;
тогда
.
Воспользовавшись формулой, выражающей разности через значения функции, получим
.
Точно так же получим
.
Аналогичные дальнейшие вычисления позволяют записать общую формулу для отыскания коэффициентов
.
Подставим найденные выражения коэффициентов в формулу (2.12)
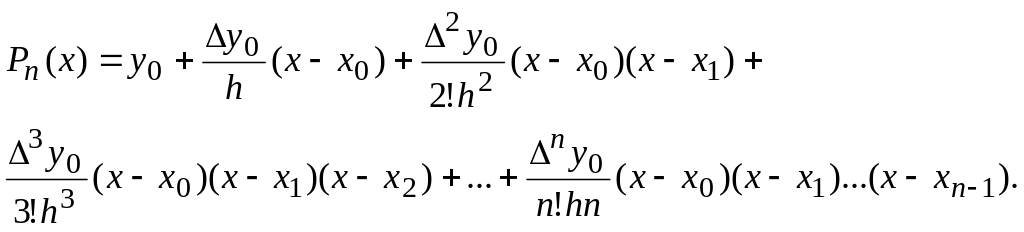
Полученный многочлен называется первым интерполяционным многочленом Ньютона.
Для практического использования многочлен Ньютона обычно записывают в несколько преобразованном виде. Чтобы получить его, введем обозначение
или
.
Множители, входящие в формулу (2.12),
выразятся через
следующим образом
,
,
……………………………….
.
Подставив эти выражения в формулу (2.12) , приведем ее к виду
(2.13)
Формулу (2.13) называют также интерполяционным многочленом Ньютона для интерполирования вперед.
Остаточный член для формулы (2.13) запишется в виде
.
(2.14)
Если есть дополнительный
узел
,
то
Формулу (2.13) выгодно использовать для
интерполирования функции
в окрестности начального значения
,
где
мало по абсолютной величине. Если в
формуле (2.13) положить
,
то получим формулу линейного
интерполирования
При будем иметь формулу параболического или квадратичного интерполирования
Пример. Построить на отрезке
с шагом
интерполяционный многочлен Ньютона
для функции
.
Решение. Составляем таблицу разностей (таблица 3)
или
,
где 
.
Таблица 3
|
|
|
|
|
3.50 3.55 3.60 3.65 3.70
|
33.115 34.813 36.598 38.475 40.447 |
1.698 1.785 1.877 1.972 |
0.087 0.092 0.095 |
0.005 0.003 |
Первый
интерполяционный многочлен Ньютона
обычно используется для вычислений в
левой половине рассматриваемой таблицы
(за
последовательно берутся
,
и т.д.) так как для
при больших значениях
разности
нельзя вычислять, не выходя за пределы
таблицы. Для правой таблицы разности
лучше вычислять справа налево и совершенно
аналогично можно получить вторую
интерполяционную формулу
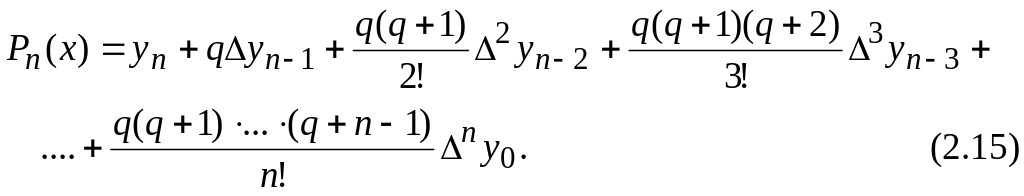
Здесь
.
Формулу (2.15) называют вторым интерполяционным многочленом Ньютона или интерполяционной формулой Ньютона для интерполирования назад.