Сопоставление интерполяционных формул Лагранжа и Ньютона. Погрешность интерполяции
Интерполяционные многочлены Лагранжа и Ньютона, построенные для одних и тех же узлов интерполяции, тождественно равны между собой, хотя и имеют различную форму записи. Это вытекает из единственности интерполяционного многочлена заданной степени. Разница в построении алгоритмов может учитываться в связи с особенностью решаемой задачи.
Коэффициенты Лагранжа
зависят от выбора узлов
и точки
,
но не зависят от вида функции
.
Это удобно, когда по заданной системе
узлов надо интерполировать несколько
различных функций.
Выбор способа интерполяции определяется различными соображениями: точностью, временем вычислений, погрешностью округлений и т.д. В ряде случаев более выгодной может оказаться локальная интерполяция, а не построение многочлена высокой степени. Во многих случаях интерполяционный многочлен
Ньютона более
удобен, чем интерполяционный многочлен
Лагранжа. Особенность этого многочлена
заключается в том, что при переходе от
многочлена
-ой
степени к многочлену
-й
степени первые
членов не меняются, а только добавляется
новый член, который равен нулю при всех
предыдущих значениях аргумента. Формула
Лагранжа этого делать не позволяет, так
как в ней добавление нового узла
заставляет заново пересчитывать все
коэффициенты
.
В точках, отличных от узлов интерполирования,
значения функций
и
не совпадают:
.
Эта разность – погрешность интерполяции
– называется остаточным членом.
Если интерполируемая функция
имеет непрерывные производные до
порядка включительно, погрешность при
замене функции
многочленом
,
т.е. величина
,
удовлетворяет неравенству
,
где
.
Если отрезок
конечен, то
.
Таким образом, если
при
растут не слишком быстро, то в этом
случае абсолютная величина погрешности
стремиться к нулю для каждого
.
В этом случае функцию
можно приблизить сколь угодно точно
полиномом Лагранжа
сразу для всех
,
если степень многочлена достаточна
велика. Как правило, увеличение числа
узлов улучшает приближение, но существуют
и отклонение от этого правила. В некоторых
случаях точность может быть повышена
за счет расположения узлов интерполяции.
Аналогично оценивается погрешность и для интерполяционной формулы Ньютона.
2.6. Интерполирование функции кубическими сплайнами
Пусть отрезок
разбит на
частей
точками
:
Сплайном
-й
степени называется
функция, представляющая собой многочлен
не выше
-й
степени на каждом из последовательно
примыкающих друг к другу интервалов
,
причем в точках стыка двух
интервалов
функция непрерывна
вместе со своими производными до порядка
не выше
.
Например, непрерывная кусочно-линейная функция (ломаная) является сплайном первой степени с производной, терпящей разрыв в точках излома.
Пусть на отрезке
определена функция
,
значения которой в точках
равны
.
Задача интерполяции функции
на отрезке
(сплайном третьей степени) состоит в
нахождении функции
,
равной
многочлену третьей степени
на каждом отрезке
,
т. е.
,
, (2.16)
причем значения сплайна в
узлах интерполяции
равны
соответствующим значениям заданной
функции
и сплайн-функция непрерывна в узлах
интерполяции вместе с производными
первого и второго порядков
(2.17)
(2.18)
(2.19)
(2.20)
Условия (2.17) - (2.20) дают
линейных алгебраических уравнений для
определения
неизвестных коэффициентов
при соответствующих
степенях
в многочленах
.
Можно показать, что интерполяционный кубический сплайн для функции существует и является единственным, если вместе с уравнениями (2.17)-(2.20) удовлетворяется какая-либо пара дополнительных условий (краевых условий) следующего типа
I.
;
II.
;
III.
.
Рассмотрим случай разбиения
отрезка
на
равных частей с шагом
,
для которого
и
.
Разберем построение
интерполяционного кубического сплайна
отдельно для условий I
и II
типов.
При построении сплайна,
удовлетворяющего краевым условиям I
типа, введем величины
,
называемые иногда
наклонами сплайна в точках (узлах)
.
Интерполяционный кубический сплайн вида
+
+
, (2.21)
удовлетворяет условиям
(2.17), (2.18), (2.19) для любых
.
Из условий (2.20) и
краевых условий I
типа можно определить
параметр
.
Действительно, легко
проверить, что
.
Кроме того, вычисления показывают, что
.
Если учесть, что
,
,
а также краевые условия I типа и условия (2.20), то получим систему из линейных уравнений относительно неизвестных
(2.22)
Решение этой системы позволяет найти значения неизвестных и определить интерполяционный сплайн в виде соотношений (2.21).
Матрица А системы (2.21) имеет порядок и является трехдиагональной
Метод Гаусса (метод исключения неизвестных) для системы (2.22) значительно упрощается и носит название метода прогонки. Прямой прогонкой находят так называемые прогоночные коэффициенты
.
Обратной прогонкой последовательно определяют неизвестные
.
Пример.
На отрезке
построить кубический сплайн с шагом
,
удовлетворяющий на концах отрезка
краевым условиям I
типа и интерполирующий функцию
.
С помощью интерполяционной формулы
вычислить приближенное значение
и сравнить его с точным.
Решение. Будем
искать кубическую параболу
,
удовлетворяющую
следующим условиям на концах отрезка
и
Подставим значения
в формулу (2.18) и получим сплайн вида
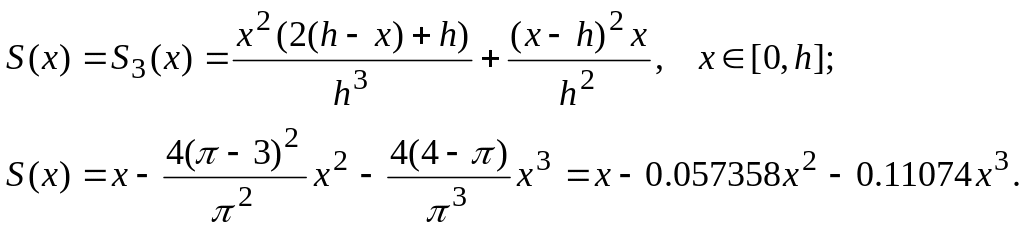
Тогда
(точное значение равно 0.5).
При построении сплайна,
удовлетворяющего краевым условиям II
типа, введем величину
-
значение второй производной сплайна в
узле
.
Уравнения (2.17), (2.18), (2.20) будут удовлетворены, если интерполяционный кубический сплайн представить в виде
+
+
,
(2.23)
.
Учитывая, что
,
,
и используя краевые условия
II
типа и условия (2.19), получим систему из
линейных уравнений относительно
неизвестных
(2.24)
Системы (2.22) и (2.24) являются частными случаями системы линейных алгебраических уравнений следующего вида
(2.25)
Для функции , имеющей на отрезке непрерывные производные до третьего порядка включительно, точность интерполяции ее кубическим сплайном по точкам равномерного разбиения отрезка с шагом при любых указанных ранее краевых условиях оценивается следующим неравенством для любых на отрезке
где
(2.26)
Неравенство (2.26) дает завышенную оценку точности приближения функции сплайном в точке.