2.2. Вычисление значений многочлена по схеме Горнера

Поскольку большинство методов аппроксимации функций сводится к замене этих функций многочленами, то одной из важнейших задач является отыскание удобного способа вычисления значения многочлена в произвольной точке. Одним из критериев удобства является уменьшение числа сложений и умножений, необходимых для вычисления многочлена.

Рассмотрим многочлен ой степени

. (2.2)

Если непосредственно вычислить значение этого многочлена в произвольной точке , то потребуется арифметических действий. При этом возникает потеря точности за счет погрешности вычисления.

Вычисление многочлена удобнее производить следующим образом. Представим его в виде

. (2.3)

Отсюда, последовательно вычисляя числа

(2.4)

находим .

Описанный метод вычисления значения многочлена в заданной точке носит название схемы Горнера. Она позволяет сократить число сложений и умножений до операций, при этом повышается точность вычисления.

Пример. Вычислить значение многочлена

при .

Решение. Имеем Последовательное применение формулы (2.4) дает

Следовательно,

Практически схему Горнера удобно реализовывать в виде следующей таблицы

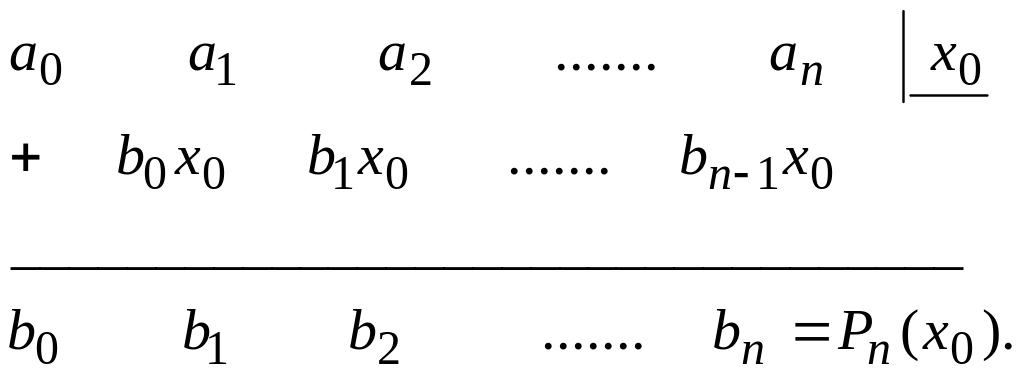
Тогда рассмотренный пример будет иметь вид

2.3. Интерполяционный многочлен Лагранжа

Будем искать многочлен степени не выше , имеющий в заданных узлах интерполяции те же значения, что и функция . Запишем этот многочлен в виде (2.2). Неизвестные коэффициенты , , …, можно найти из условия . Это условие приводит к системе линейных уравнений

(2.5)

Определитель этой системы

называется определителем Ван-дер-Монда. Он отличен от нуля, так как все узлы интерполирования различны. Следовательно, система (2.5) имеет единственное решение и интерполяционный многочлен определяется единственным образом. Однако, для большого числа узлов интерполяции, решать эту систему сложно. Многочлен можно построить другим способом: строятся

многочленов таких, что

Так как искомый многочлен обращается в нуль в точках , то он имеет вид

, (2.6)

где - постоянный коэффициент. Полагая в формуле (2.6) и учитывая, что , получим

Отсюда

.

Подставив это значение в формулу (2.6), будем иметь

. (2.7)

Тогда, многочлен , удовлетворяющий условиям , имеет вид

. (2.8)

Подставив в формулу (2.8) значение из (2.7), получим

. (2.9)

Многочлен , определяемый по формуле (2.9) , называется интерполяционным многочленом Лагранжа. Очевидно, что степень многочлена Лагранжа не превышает числа . Часто многочлен Лагранжа записывают виде

.

При имеем две точки, и формула Лагранжа представляет в этом случае уравнение прямой , проходящей через две заданные точки

,

где - абсциссы этих точек.

При получим уравнение параболы , проходящей через три точки

.

Пример. Для функции построить интерполяционный многочлен Лагранжа, выбрав узлы

Решение. Многочлен Лагранжа для трех узлов интерполирования запишется так

Вычисляем соответствующие значения функции

Применяя формулу Лагранжа, получим

или