8.4. Численные решение систем дифференциальных уравнений первого порядка
Пусть дана система двух дифференциальных уравнений первого порядка:
(8.8)
Решением системы (8.8) называется пара
функций
и
,
при подстановке которых в систему
получаются тождества.
Решению
системы уравнений (8.8) соответствует
интегральная кривая в пространстве
трех измерений
.
Условия, при которых через каждую точку
некоторой области
трехмерного пространства проходит
единственная интегральная кривая,
содержится в теореме существования и
единственности решения.
Теорема. Если функции
и
- правые части дифференциальных уравнений
системы (8.8) – непрерывны вместе со
своими частными производными по
переменным
и
в некоторой области
трехмерного пространства, то для любой
точки (
система (8.8) имеет единственное решение,
удовлетворяющее начальным условиям
. (8.9)
Задачи Коши для системы состоит в нахождении решения системы (8.8), удовлетворяющего начальным условиям (8.9).
Если ввести векторные обозначения
,
,
,
,
то задача Коши (8.8)-(8.9) в векторной форме
запишется так:
, 
. (8.10)
Численное решение задачи Коши (8.10)
состоит в том, что на сетке отрезка
требуется получить приближенные значения
координат вектора
в узлах сетки
Обозначим вектор, аппроксимирующий
решение через
,
а его координаты – через
так, что
.
Будем искать решение на равномерной
сетке с шагом
Величина погрешности численного метода
оценивается величиной
,
где
- погрешность решения на сетке с шагом
в точке
:
Практически погрешность в точке
оценивается по формуле Рунге. Пусть
,
- значение численного решения в точке
,
полученные для шагов
и
соответственно; тогда погрешность
в точке
для вычислений с шагом
выражается приближенно равенством
,
(8.11)
где
- порядок точности численного метода.
Численное решение задачи Коши (8.10) для системы дифференциальных уравнений находится с помощью классического метода Рунге-Кутта четвертого порядка. Векторная форма алгоритма метода Рунге-Кутта для задачи (8.10) соответствует рекуррентным формулам (8.7) и имеет вид
(8.12)
где векторы
Пример. Найти численное решение задачи Коши для системы двух дифференциальных уравнений
на сетке
отрезка
методом Рунге-Кутта. Вычисления провести
с шагами
и
.
Оценить погрешность по принципу Рунге.
Сравнить численное решение с
аналитическим решением
Решение. Здесь
,
,
Численное решение будем искать по формулам (8.12).
Последовательно
вычисляя, при
и
имеем
; 
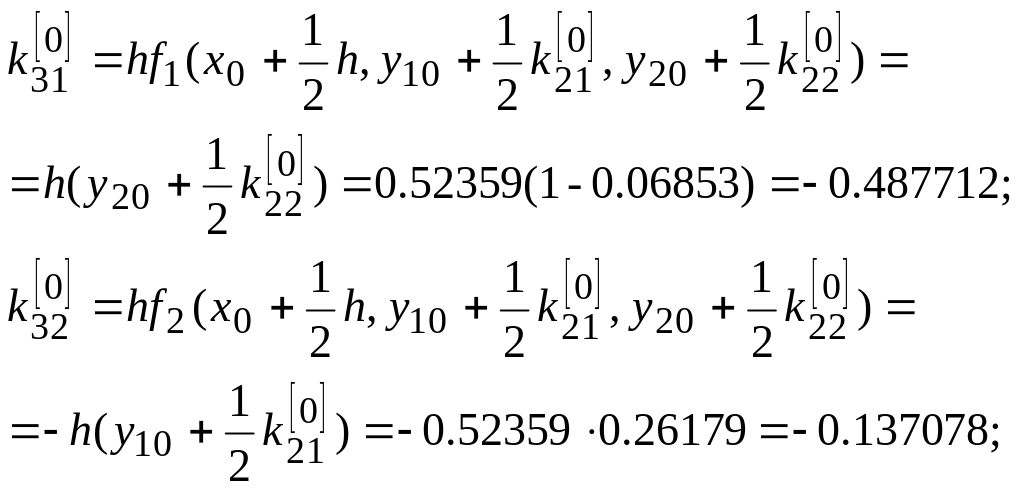
Продолжая процесс вычислений, получаем
Результаты численного решения задачи с шагами и сведены в таблицу 11.
Таблица 11
|
|
Численное решение задачи Коши
|
Точное решение
|
|||
с шагом |
с шагом |
|||||
|
|
|
|
|||
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
0.49967 |
0.86605 |
0.49998 |
0.86603 |
0.5 |
2 |
|
0.86548 |
0.50037 |
0.86599 |
0.50003 |
0.86625 |
3 |
|
0.99958 |
0.00088 |
0.99998 |
0.00006 |
1 |
Используя правило Рунге, находим погрешность
