2. Метод половинного деления

Пусть дано уравнение (4.1), причем функция непрерывна на и (рис 11). Для вычисления корня уравнения (4.1), принадлежащего отрезку , найдем середину этого отрезка . Если , то для продолжения вычислений выберем ту из частей данного отрезка или , на концах которой функция имеет противоположные знаки. Концы нового отрезка обозначим через (рис 2).

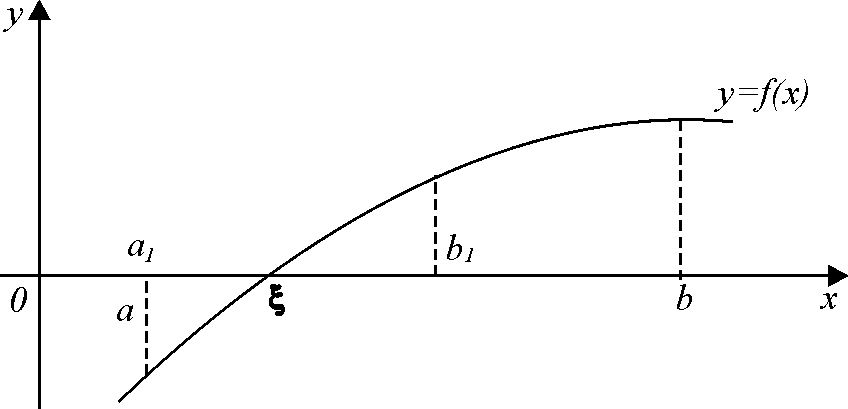
Рис.2

Новый суженный промежуток снова делим пополам и проводим те же рассмотрения и т. д. В результате получаем на каком-то этапе или точный корень уравнения (4.1), или же бесконечную последовательность вложенных отрезков , , …, , таких, что

( ), (4.2)

. (4.3)

Число – общий предел последовательностей и – является корнем уравнения .

Оценку погрешности на -ом шаге вычислений можно получить из соотношения (4.3) в виде

. (4.4)

Здесь с точностью , не превышающей .

Метод деления пополам сходится для любых непрерывных функций, устойчив к ошибкам округления и легко реализуется на ПЭВМ.

Пример. Методом половинного деления с точностью найти корень уравнения ( ).

Решение. В предыдущем примере при отделении корней уравнения было установлено, что искомый корень принадлежит отрезку . На каждом шаге вычислений значение корня принимаем равным с погрешностью . Будем производить вычисления и выбирать последовательность вложенных отрезков , используя условие . Имеем Так как , то полагаем Тогда

Здесь , следовательно, Тогда

Производя вычисления далее, можно убедиться, что заданная точность достигается на 7-ом шаге: с погрешностью

4.3. Метод хорд

Пусть дано уравнение (4.1), где – непрерывная дважды дифференцируемая функция на отрезке . Пусть для определенности при . Тогда кривая будет выпукла вниз. Возможны два случая: 1) (рис.3)

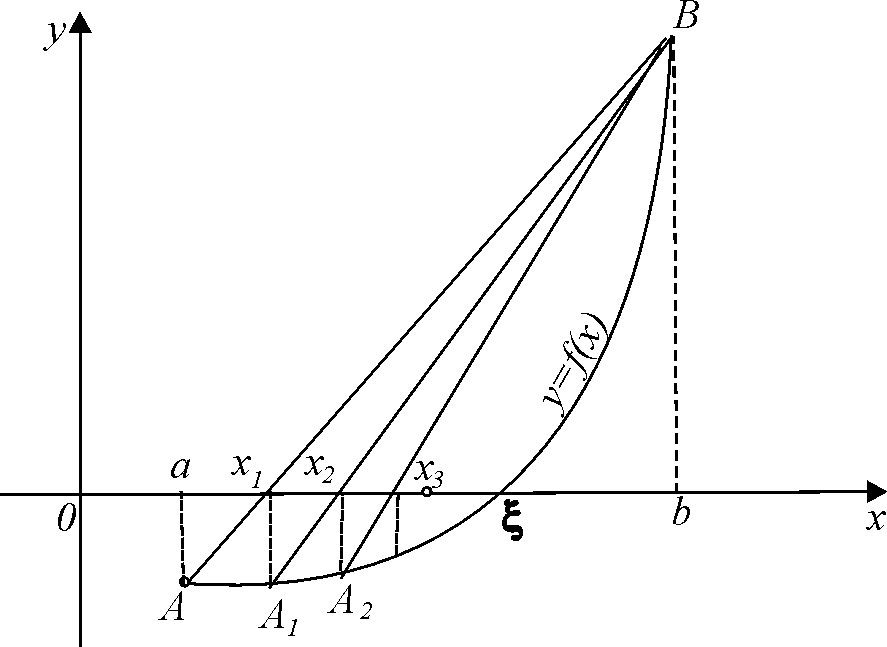
Рис. 3

2) (рис. 4).

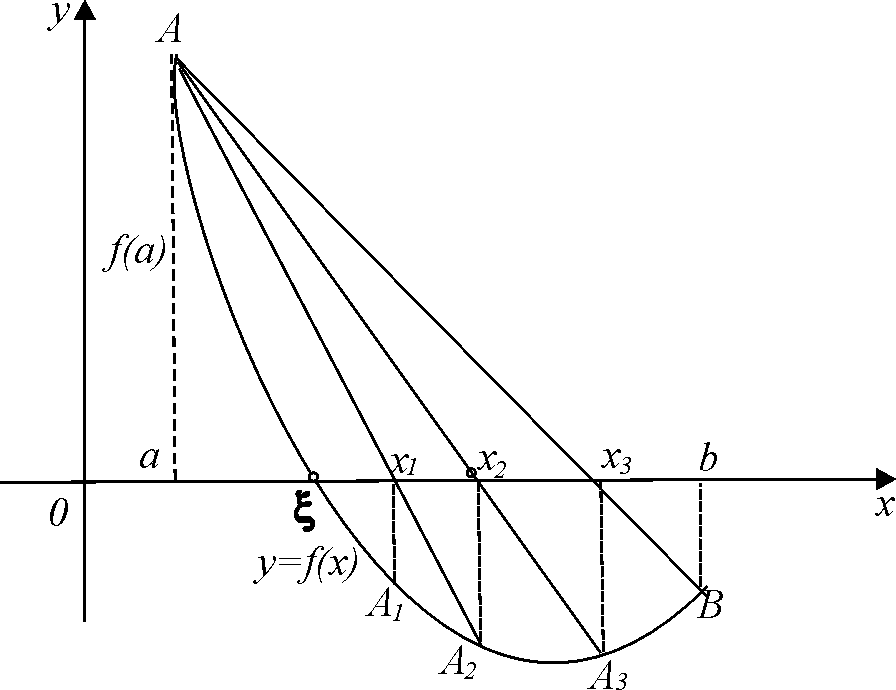
Рис. 4

Проведем хорду , соединяющую концы кривой . За приближенное значение искомого корня примем абсциссу точки пересечения этой хорды с осью . Для разыскания этого приближенного значения напишем уравнение прямой , проходящей через две заданные точки и : . Так как при , то, следовательно, , откуда .

Чтобы получить более точные значения корня, определяем . Если , тогда за новый промежуток изоляции корня можно принять . Соединив точки и , получим в точке пересечения хорды с осью второе приближение , которое вычислим по формуле . Если же , то применим эту формулу к отрезку . Повторяя этот прием несколько раз, будем получать все более точные значения корня и т.д.

В первом случае конец отрезка изоляции неподвижен и последовательные приближения корня находятся по формуле

. (4.5)

Во втором случае неподвижен конец , а последовательные приближения имеют вид

. (4.6)

Если - точный корень уравнения (4.1), изолированный на отрезке , а - приближенное значение корня, найденное методом хорд, то оценка погрешности этого приближенного значения такова:

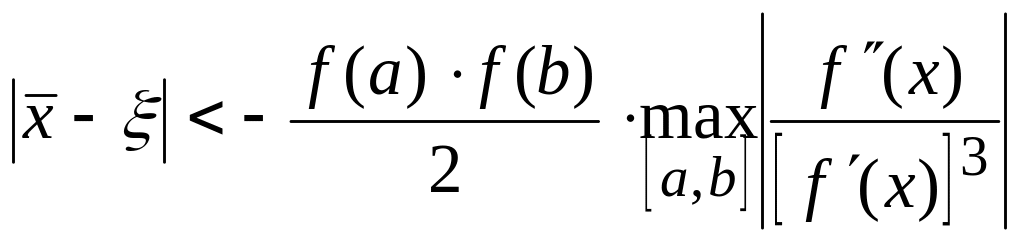. (4.7)

Пример. Методом хорд найти положительный корень уравнения с точностью до .

Решение. Найдем интервал изоляции корня. Так как и , то искомый корень лежит в интервале (1,2). Для того чтобы уменьшить количество вычислений разделим этот интервал пополам. Так как , . Последовательно применяя формулу (4.5), будем иметь

Так как и при имеем , то можно принять

.

Таким образом, , где .