
Учебное пособие 2015
.pdf
(кривая Z1 ) представлены на рис. 2.8. Эти переходные
процессы просчитаны на ЦВМ «Киев» по формулам (2.23) — (2.25). Таким методом в [63] с помощью моделирования динамики на ЦВМ было произведено сравнение релейноимпульсных регуляторов с пропорциональными регуляторами с синхронным детектором.
Исследования пропорциональной разностной ИЭС (2-й тип) и релейной ИЭС с импульсной коррекцией (1-й тип), проведенные на ЦВМ «Киев», показали:
1.Релейные системы, в частности системы с импульсной коррекцией, предпочтительнее применять при скачке возмущения, особенно в случае значительных рассогласований. Хотя в системах 1-го и 2-го типов в этом случае переходные процессы оканчиваются приблизительно за одинаковый интервал времени, но в системе 1-го типа они протекают значительно более плавно и с меньшей динамической ошибкой, чем в системе 2-го типа.
2.Пропорциональные системы с модуляцией (2-й тип) предпочтительнее применять в условиях дрейфа экстремума с постоянной скоростью β, так как они допускают значительно большие скорости дрейфа экстремума без потери устойчивости, чем системы 1-го типа.
3.Выяснены некоторые интересные особенности динамики системы 2-го типа. Зависимость критической скорости дрейфа экстремума (при превышении которой движения ИЭС становятся расходящимися) от коэффициента усиления регулятора β = f (k) имеет экстремальный характер.
При этом коэффициенту усиления k0 , при котором
критическая скорость дрейфа максимальна, соответствует наиболее короткий по времени переходный процесс при скачке возмущения. Это положение может быть рекомендова-
131
но как практическое правило настройки регулятора 2-го типа для работы в условиях значительных скоростей дрейфа экстремума.
2.2.2. Метод построения переходных процессов в импульсных экстремальных системах
В основе этого метода, предложенного Ю. С. Попковым [48], лежит связь между дискретным преобразованием Лапласа координаты z на выходе объекта, имеющего ту же структуру,
Рис. 2.9. Релейно-импульсная экстремальная система: ФПЭ — формирователь показателя экстремума ( u y zn zmax
—для системы с запоминанием экстремума; uy zn — для
системы с переключением по величине и знаку первой разности); РЭ — релейный элемент; ИУ — исполнительное устройство.
что и в предыдущем случае (рис. 2.9), и входной координатой исполнительного устройства (выходом регулятора) и. Эта связь выражается следующей формулой, полученной в [47]:
132
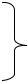
|
|
|
|
|
|
1 |
|
|
1 |
C j |
|
|
|
Z (q, e) k |
|
|
W (q, ) |
|
W |
(q , ) |
|||||||
0 |
|
||||||||||||
|
|||||||||||||
|
|
|
|
|
|
2 |
2 j |
|
1Э |
(2.26) |
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
0 |
|
|
|
C j |
|
|
|
W (q q , )U (q )U (q q )dq d, , |
|
||||||||||||
|
|
1Э |
|
|
|
|
|
|
|
|
|
|
|
где k |
0 |
k |
H |
k 2 Т,W |
|
(q, ) D W (q),W |
|
(q) ; |
|||||
|
|
И |
|
1Э |
|
1 |
ИY |
|
|
||||
q=pT (p- параметр преобразования Лапласа); Т — интервал дискретности;
k И — коэффициент усиления импульсного элемента; k H — коэффициент при параболе.
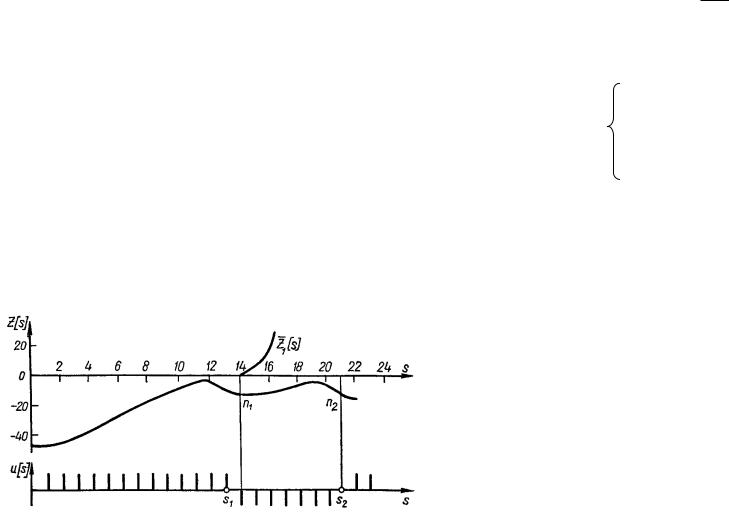
При этом uS = Ф (z [s]) — закон регулирования регулятора U m представляет собою последовательность серий мгновенных импульсов с площадью k p (рис. 2.10). Перемена
знака этих импульсов происходит при выполнении соответствующих условий переключения. Для систем с запоминанием экстремума (переключение по величине и знаку отклонения от экстремума) условия переключения заключаются в следующем:
z sk zmax |
, |
|
z sk 1 , |
(к=1, 2, …), |
(2.27а) |
а для систем с переключением по величине и знаку первой разности показателя экстремума имеем
z sk |
, |
|
z sk 1 , |
(к=1, 2, …), |
(2.27б) |
где — зона нечувствительности релейного элемента (РЭ). Преобразования (2.27a) или (2.276) осуществляются над
выходным сигналом объекта с помощью блока формиро-
вателя показателя экстремума ФПЭ и релейного элемента РЭ (рис. 2.9), неоднозначная характеристика которого определяется также выражением (2.27a) или (2.276) [37].
В [48] показано, что последовательность управляющих импульсов и [s] может быть представлена в виде
|
|
|
|
|
|
|
m 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
u[s] kP (1[s] 2 ( 1)i 1[s si ]) , |
(m=1, 2, …). |
(2.28) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если же um [s] известен, то um 1 [s] на интервале |
|
|||||||||||||||||||||||||
sm s sm 1 имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
u |
m |
[s] u |
m |
[s] 2k |
P |
( 1)m [s s |
m |
]. |
|
|
|
(2.29) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Допустим, что um [s] известно, тогда определим реакцию |
||||||||||||||||||||||||||
системы на серию импульсов um 1[s] . Переходя в (2.85) от |
||||||||||||||||||||||||||
оригиналов к изображениям, получим |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
U |
|
(q) U |
|
(q) 2( 1)m e qS mU |
(q), |
|
|
|
(2.30) |
|||||||||||||||||
m 1 |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||
|
|
где |
|
|
|
|
|
|
|
U (q) k |
|
|
|
|
eq |
|
|
. |
|
|||||||
|
|
|
|
|
|
|
|
|
P |
|
eq |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
||||||
Подставив (2.30) в (2.26), имеем |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Z |
|
(q, ) Z |
(q, ) Z |
(q, ), |
|
|
|
|
(2.31) |
|||||||||||||||||
|
|
m 1 |
|
|
|
|
|
|
m |
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
C j |
|
|
|
|
||||
Z (q, ) k |
|
|
|
W |
|
(q, ) |
|
|
|
|
|
|
W |
|
(q , ) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
0 |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
m |
|
|
|
|
|
|
|
|
|
2 |
j |
|
|
|
1Э |
|
|
(2.32) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
||||
W |
(q q , )U |
(q )U |
(q q )dq d, |
|
|
|
|
|||||||||||||||||||
1Э |
|
|
|
|
|
|
|
|
m |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
134 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
133
|
|
|
1 |
|
1 |
C j |
|
|
|
|
Z |
(q, ) k |
|
|
W (q, ) |
|
W |
(q , )W |
(q q , ) |
||
0 |
|
|||||||||
|
||||||||||
m |
|
2 |
2 j |
|
1Э |
1Э |
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
C j |
|
|
|
|
[4e qS mU (q )U (q q ) 4e qSU (q )U (q q )]dq d. |
||||||||||
|
0 |
|
|
0 |
|
0 |
|
|
0 |
|
(2.33)
Далее в (2.31) можно перейти к оригиналам, полагая ε =0, и получить рекуррентное уравнение переходного процесса
|
|
|
|
|
zm 1[s] zm [s] zm [s] |
(m=1, 2, …), |
|
||
z [s] D 1{z (q)}, |
(2.34) |
|||
1 |
|
|
0 |
|
где z0 определяется из (2.32) при Т = 0.
Переходный процесс строится следующим образом. Определяется вначале z1 [s] на интервале s0 0 s s1 .
Момент s1 определяется по выполнении условий переключения (2.27). Затем находим z1 (q, ) по формуле(2.33) и, переходя
Рис 2.10 Переходный процесс в РИЭС.
135
от (2.33) к оригиналам, получаем z1 [s]. Зная z1 [s], определяем в интервале
s1 s2 , z2 [s] z1[s] z1[s] и т д.
Таким образом, переходный процесс строится до наступления периодического режима по таким рекуррентным формулам
|
z1[s] |
|||||
|
|
|
|
|
|
|
z[s]= |
z1[s] z1[s] z2 [s] |
|||||
.......... .......... .......... |
||||||
|
||||||
|
|
|
|
|||
|
zk 1[s] zk [s] zk [s] |
|||||
(s0 0 s s1 ), |
|
|
(s1 s s2 ), |
(2.35) |
|
.......... .......... ...... |
||
|
||
(sr 1 s sr ) |
|
На рис. 2.10 показан переходный процесс в релейноимпульсной СЭР, построенный указанным выше способом.
2.2.3. Исследование свободных и вынужденных движений в импульсных-экстремальных системах.
Условимся называть свободными движениями ИСЭР движение системы при неподвижном экстремуме, а вынужденными движениями — движение системы при перемещении точки экстремума с постоянной скоростью.
Рассмотрим импульсные экстремальные системы с синхронным детектором или с модуляцией (ИЭСМ).
Динамика ИЭСМ описывается нелинейными разностными уравнениями с переменными коэффициентами
[28, 63].
Основная задача при исследовании свободных движений ИЭСМ заключается в отыскании областей устойчивости этих движений.
136
Применить критерий Попова — Цыпкина для решения этой задачи невозможно, так как данный критерий накладывает на нелинейности ограничения вида
r |
Ф1 |
(x, p) |
k r k |
|
, |
(2.36) |
|
x |
0 |
||||
|
|
|
|
|
|
|
|
Ф1 (x, p) 0, |
|
|
(2.37) |
||
что равносильно требованию о принадлежности характеристики нелинейного и нестационарного элемента Ф1 (x, p) сектору k + r= k0
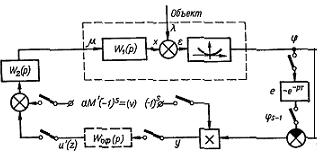
Рис 2.11 Схема ИЭСМ.
|
e ST - элемент запаздывания на один такт, W (s) - |
|||||||||
|
|
|
|
|
|
|
|
|
|
1 |
линейное инерционное звено, |
|
|
|
|
||||||
|
I – синхронный детектор, W2 (s) - сервомотор, Wоф (s) - |
|||||||||
фильтр с фиксатором нулевого порядка, |
|
|||||||||
W (s) |
k(1 e ST ) |
, a |
|
( 1)n |
a |
|
cos n |
модуляция. |
||
|
|
M |
M |
|||||||
оф |
|
s( |
ф s 1) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
137
Вработах по исследованию экстремальных систем обычно аппроксимируют экстремальную характеристику объекта параболой. Последняя не удовлетворяет условию (2.36), что и послужило причиной применения иных методов для исследования устойчивости ИЭСМ.
Математически строгое решение задачи об устойчивости ИЭСМ с помощью второго метода А. М. Ляпунова, по которому получаются достаточные условия устойчивости системы, произведено В. М. Кунцевичем [30]. Однако результаты [30] легко обозримы лишь для ИЭСМ с линейной частью, имеющей порядок не выше второго. Здесь будет из ложен менее строгий, приближенный метод анализа устойчивости ИЭСМ, который не накладывает ограничений на порядок линейной части системы [64].
В[64] рассматривается ИЭСМ разностного типа [28, 63], схема, которой приведена на рис. 2.11.
Объект экстремального управления представим в виде
последовательного соединения линейного инерционного звена с передаточной функцией W1 ( p) и нелинейного безынерционного звена с экстремальной характеристикой
(2.94)
где ε - ошибка системы (ε = х + λ);
х- выходная координата линейного звена;
λ- возмущение;
aH - крутизна параболы. Представим сигнал ошибки в
виде двух составляющих |
|
|
|
ε=e+m |
(2.39) |
||
Здесь |
|
|
|
e( p) W ( p)W |
2 |
( p)u (z) ( p); |
(2.40) |
1 |
|
|
|
|
|
138 |
|
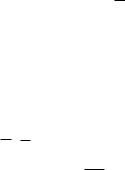
m( p) W ( p)W |
( p) (z). |
(2.41) |
|
1 |
2 |
|
|
Очевидно, что (2.41) — уравнение сигнала модуляции, приведенного к входу нелинейного безынерционного звена. В дальнейшем будем интересоваться только составляющей сигнала ошибки е.
2.2.4. Исследование устойчивости свободных движений ИЭСМ.
В [28] получено нелинейное разностное уравнение, описывающее динамику данной ИЭСМ, которое имеет вид
[2a |
M |
a |
W (E)(E 1) E]e |
S |
W |
Л |
(E)[( 1)S a |
H |
(e2 |
e2 )] |
S 1 |
, |
|
|
|
H Л |
|
|
S 1 |
S |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
(2.42) |
||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
WЛ (E) W1W2 (E) - |
линейная часть системы. |
(2.43) |
||||||||
При наличии фильтра с фиксатором нулевого порядка (используемого в ИЭСМ для фильтрации квазипериодических составляющих) с передаточной функцией
Wоф ( p) |
1 e PT |
|
(2.44) |
|
p( Ф p 1) |
||||
|
|
|||
линейная часть имеет вид |
|
|
|
|
WЛ (E) Wоф (E)W1W2 (E). |
(2.45) |
|||
При исследовании устойчивости свободных движений ИЭСМ полагаем λ = 0. Тогда уравнение (2.42) превращается в однородное. Нетрудно преобразовать его к виду
139
|
|
1 |
e |
|
a |
|
(e |
|
)2 ( 1)S 0 , |
|
(2.46) |
||
|
|
|
S |
H |
S |
|
|||||||
W (E) |
|
||||||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
Э |
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
||
WЭ |
(E) |
|
|
|
WЛ |
(E)(E 1) |
. |
(2.47) |
|||||
2aM aH WЛ (E)(E 1) E |
|||||||||||||
|
|
|
|
|
|
||||||||
Нетрудно заметить, что (2.37) соответствует структурная схема, приведенная на рис. 2. 12, а.
Таким образом, ИЭСМ сводится к системе, в которой имеется эквивалентная линейная импульсная часть (ЛИЧ) WЭ (E) , нелинейное безынерционное звено и синхронный
детектор — звено с периодически изменяющимся параметром. Используя метод А. Леонарда [31], разработанный для
исследования устойчивости параметрических колебаний в линейной непрерывной системе с помощью описывающих функций, получим условия самовозбуждения ИЭСМ, т. е. нахождения системы на границе устойчивости, на
фиксированных частотах ω: π/2, π/3, π/4, π/6 ( T ), так как
именно на этих частотах и возникают колебания в импульсных экстремальных системах. Заметим, что (2.47) соответствует дискретное преобразование
W (z) |
|
|
W (z)(z 1) |
|
|
||
|
|
|
|
Л |
. |
(2.48) |
|
|
|
|
|
|
|||
Э |
2a |
|
a |
|
W (z)(z 1) z |
|
|
|
M |
H |
|
|
|||
|
|
|
Л |
|
|
||
Подставив вместо z e j ( T ) , получим частотную
характеристику эквивалентной ЛИЧ WЭ ( j ) , которую можно представить в виде
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
( |
|
)e j Э ( ) , (2.49) |
||
W ( j ) G |
( ) jB |
( ) M |
|
||||||||||
Э |
|
Э |
|
|
Э |
|
|
Э |
|
|
|
|
|
|
|
|
140 |
|
|
|
|
|
|
|
|||
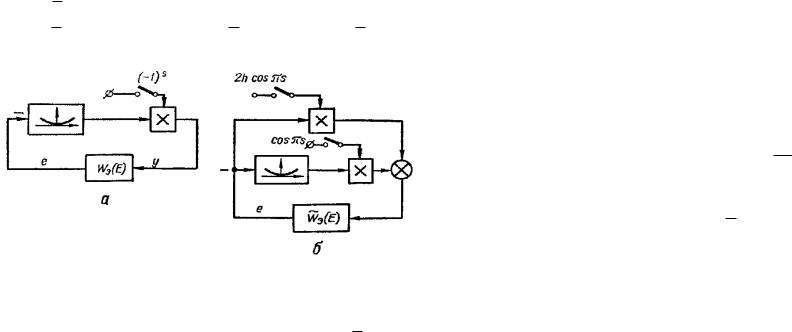
где GЭ ( ) — вещественная часть частотной характеристики;
BЭ ( ) — мнимая часть; M Э ( ) — модуль; Э ( ) — аргумент.
Рис. 2.12.
Применив метод А. Леонарда к системе, приведенной на рис. 2.12,а, получим условие самовозбуждения ИЭСМ
(нахождение на границе устойчивости) на частотах : π/2, π/3, π/4, π/6 соответственно
|
|
G |
( ) [a2 e2 M (0)] 1 |
, |
(2.50) |
|||||||||||||||
|
|
|
|
Э |
2 |
|
H |
|
0 |
|
|
|
|
Э |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
G ( ) 2[a2 |
|
e2 |
|
] 1 , |
|
|
(2.51) |
||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
Э |
3 |
|
H |
|
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
G |
( ) 2[a2 e2 M |
|
( )] 1 , |
|
(2.52) |
|||||||||||||||
|
Э |
|
4 |
H |
0 |
|
|
Э |
|
2 |
|
|
|
|||||||
|
|
|
|
|
) 2[a |
2 |
|
2 |
|
|
|
|
|
|
2 |
1 |
, |
(2.53) |
||
G |
Э |
( |
|
H |
e |
0 |
M |
Э |
( |
|
)] |
|||||||||
6 |
3 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где e0 — начальное отклонение системы.
141
Выражения (2.50) — (2.53) представляют собою условия самовозбуждения на частотах, которые имели место в большом количестве конкретных примеров. Из (2.52), (2.53) следует, что условием самовозбуждения ИЭСМ является равенство вещественной части эквивалентной ЛИЧ отрицательной величине, определяемой по формулам (2.50)—( 2.53) Поэтому определение величины критического начального отклонения eokp можно произвести следующим
образом. Определяется вид WЭ ( j ) из выражения (2.48) с
учетом (2.45) и (2.46). Находится точка частотной характеристики, имеющая наибольшую отрицательную
вещественную часть GЭ ( ) . В зависимости от того, какая частота ω соответствует этой точке, находят величину критического начального отклонения eokp по одной из формул
(2.50) — (2.53). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Рассмотрим ИЭСМ при |
|
|
|
|
|
|
|
|||||||||
W ( p) |
|
|
|
|
, W ( p) |
1 |
;W ( p) 1 . |
|||||||||
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
|
p |
1 |
|
2 |
|
p |
|
|
оф |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
z(1 d ) |
|
|
|
|
|
T |
|
|||
Тогда W W |
2 |
(z) |
|
, d e |
. |
|||||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
|
(z 1)(z d ) |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставляя W |
(z) W W (z) |
в (11.104), получим W (z) |
||||||||||||||
|
|
|
Л |
|
|
|
|
1 2 |
|
|
|
|
|
|
Э |
|
в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W (z) |
(z 1) |
, |
(2.54) |
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Э |
|
|
z 2 z |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где
142
a(1 d ), 2aM aH (1 d ) 1 d ,
2aM aH (1 d ) d . |
(2.55) |
При этом величина aM (амплитуда модуляции, пересчитанная к входу нелинейного звена) определяется по
заданной величине амплитуды модуляции a |
и равна в |
|||
|
|
|
M |
|
нашем случае |
|
|
|
|
a |
|
a |
(1 d ) |
(2.56) |
|
|
|||
|
M |
M 2(1 d ) |
|
|
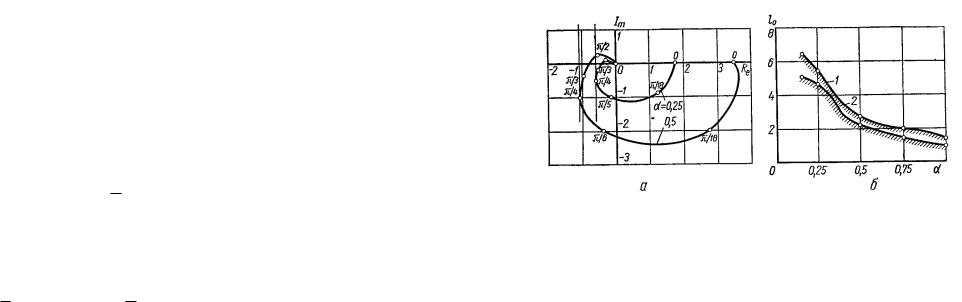
Заменив z на e j (2.53), получим амплитудно-фазовую характеристику. На рис.11.13,а сплошными линиями изображена амплитудно-фазовая характеристика для aM = 1,
d = 0,3 и при значениях α, равных соответственно 0,25 и 0,5. Нетрудно заметить, что величине наибольшей отрицательной
GЭ ( ) соответствует 4 . На рис. 2.13 показана область
устойчивости для ИЭСМ в плоскости α (коэффициент усиления линейной части) — e0 (начальное отклонение) определенная с помощью численного решения уравнения динамики при различных отклонениях e0 , полученного в [28],
а также по выражениям (2.50) — (2.53). Расхождение составляет около 20%. Как следует из (2.50) — (2.53), а также из разобранных выше примеров, требование абсолютной устойчивости в смысле [70] является очень жестким для ИЭСМ, так как последняя возвращается в состояние равновесия из начального отклонения e0 меньше некоторого
критического значения eokp определяемого из (2.50) - (2.53).
143
Рис. 2.13.
Из (2.48) следует, что WЭ ( j ) 0 . Отсюда можно
утверждать, что колебания е с частотой модуляции π невозможны.
2.2..5. Исследование устойчивости вынужденных движений ИЭСМ.
При исследовании вынужденных движений экстремальных следящих систем принимают что возмущение λ (см. рис. 2.1), смещающее точку экстремума вдоль оси регулирующих воздействий изменяется по линейнонарастающему закону S =βS. Когда скорость нарастания
возмущения β превосходит некоторую величину движение экстремальной системы расходящееся.
Определим критическую величину kp . Предлагаемая
ниже методика будет рассматриваться для ИЭСМ с линейной частью второго порядка, однако метод не накладывает
144
ограничений на порядок линейной части. |
|
|
|
|
|
||||||||||
|
Для ИЭСМ с W ( p) |
|
|
, W ( p) |
1 |
; |
W ( p) 1 |
||||||||
|
|
|
|
|
|||||||||||
|
|
|
1 |
|
|
|
|
p 1 |
2 |
|
|
p |
оф |
||
|
|
|
|
|
|
|
|
|
|
|
|||||
уравнение динамики можно получить [28] в виде |
|||||||||||||||
e |
S 2 |
( 1)S e |
S |
1 |
e |
S 1 |
( 1)S e |
S |
|
(1 d ), (2.57) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
где ξ, ζ, δ, определяются из (2.55). |
|
|
|
|
|
||||||||||
|
Представим решение этого нелинейного разностного |
||||||||||||||
уравнения в виде двух компонент |
|
|
|
|
|
||||||||||
|
|
|
|
eS |
h eS |
|
|
|
|
(2.58) |
|||||
Первая компонента представляет собою установившееся значение сигнала ошибки — скоростную ошибку экстремальной следящей системы. Она выражается [28] через скорость дрейфа и добротность экстремальной следящей системы
h [4a |
M |
a |
H |
] 1 . |
(2.59) |
|
|
|
|
Вторая компонента является вариацией или отклонением ошибки от установившегося значения. Исследование устойчивости вынужденного движения сводится к исследованию условий затухания отклонения ошибки от
установившегося значения [70]. |
|
|
|
|
|
|||||||
Подставляя (2.58) в (2. |
|
|
|
57), получим уравнение |
||||||||
h e |
S 2 |
h e |
S 1 |
( 1)S (h e |
S 1 |
)2 |
|
h |
||||
|
|
|
|
|
|
|
|
(2.60) |
||||
e |
|
( 1)S (h |
e |
|
)2 |
(1 d ) . |
|
|
|
|||
S |
S |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
Вычитая (2.60) из (2.57) с учетом (2.58), получим уравнение в вариациях
e |
S 2 |
e |
S 1 |
|
|
e |
S |
2h ( 1)S ( e |
S 1 |
|
e |
S |
) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.61) |
||||||
( 1)S ( e2 |
|
e |
2 ) 0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
S 1 |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
||
Уравнение (2.61) представляет собою однородное |
||||||||||||||||||||
нелинейное разностное уравнение с переменными |
|
|
|
|
||||||||||||||||
параметрами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Его нетрудно преобразовать к виду |
|
|
|
|
|
|
||||||||||||||
|
E 2 |
E |
e |
|
2h( 1)S e |
|
( 1)S e2 |
0. (2.82) |
||||||||||||
|
|
|
|
|
S |
S |
||||||||||||||
|
|
|
|
|
||||||||||||||||
|
(E 1) |
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Обозначим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
~ |
|
|
|
|
(E 1) |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
W (E) |
|
|
|
|
|
|
. |
|
|
|
|
|
(2.63) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Э |
|
|
E 2 E |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
~ |
(E) тождественна |
W |
|
(E) для |
||||||
Нетрудно заметить, чтоW |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Э |
|
|
|
|
|
|
|
Э |
|
|
линейной части второго порядка, которая определяется из
(2.54).
Уравнению (2.62) соответствует структурная схема рис.
2.37, б.
Пользуясь описанной методикой А. Леонарда применительно к системе, изображенной на рис. 2.37, б, можно получить условие самовозбуждения для вариации e0
на различных частотах.
Условия самовозбуждения вынужденных движений ИЭСМ следующие
~ |
|
|
aH2 |
~ |
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
GЭ |
|
|
e02 M Э (0) |
|
|
(2aM aH ) 1 |
, |
(2.64) |
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
146
145
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
2 |
|
|
|
|
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
GЭ |
|
|
2 |
|
e0 |
aH |
2 M |
Э |
|
|
|
|
|
(2aM aH ) 2 |
|
, |
(2.65) |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
1 |
||
~ |
|
|
|
|
|
|
~ |
|
|
|
|
~ |
|
|
|
3 |
|
|
|
|||||||||||
GЭ |
|
|
2 aH2 |
|
e02 M |
Э |
2 M |
Э |
|
|
|
|
(2aM aH ) 2 |
|
(2.66) |
|||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|||||
|
~ |
|
|
|
|
|
|
|
|
|
~ |
2 |
|
|
|
|
|
~ |
5 |
|
|
|
|
1 |
||||||
GЭ |
|
|
2 aH2 e02 M |
Э |
|
|
2 M |
Э |
|
(2aM aH ) 2 |
||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.67) |
Нетрудно заметить, что (2.64)—( 2.67) являются обобщением выражений (2.50) — (2.53). Действительно, (2.64)—(2.67) дают ответ на вопрос об устойчивости ИЭСМ как при начальном отклонении e0 , так и при наличии
линейно-нарастающего дрейфа со скоростью β. Полагая β=0, получим величину критического начального отклонения, а, приняв e0 = 0, получим критическую скорость дрейфа
экстремума.
В качестве примера рассмотрена ИЭСМ со следующей
настройкой a |
=3,5; d = 0,3; коэффициенты усиления 0,25; |
M |
|
0,5; 0,75 и 1,0 соответственно. Для первых трех коэффициентов усиления частотной характеристики WЭ ( j ) построены на рис. 2.13, а. Рассчитанные по формулам (2.64) — (2.67) при e0 критические скорости дрейфа в зависимости
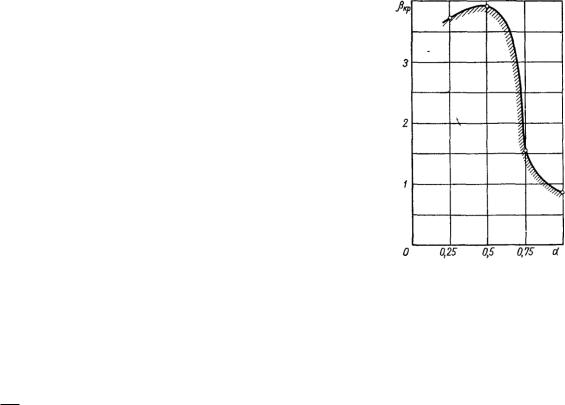
от коэффициента усиления представлены на рис. 2.14.
Из рис. 2.14. видно, что имеется коэффициент усиления, при котором запас устойчивости максимален. Это хорошо согласуется с результатами моделирования рассматриваемой
147
ИЭСМ на ЦВМ «Киев»
[63].
Легко показать, что в случае, когда линейное инерционное звено стоит за экстремальным безынерционным звеном, то все изложенные рассуждения остаются в силе. Отличие заключается в том, что передаточная функция линейной части
системы WЛ (z) в (2.48) имеет в данном случае вид
|
|
Рис.11.14.Область |
|
||
|
|
устойчивости вынужденных |
|||
|
|
движений ИЭСМ при |
|||
|
|
a |
=3,5; d = 0,3. |
|
|
|
|
M |
|
|
|
W (z) W W (z)W (z), гдеW ( p) |
1 e pT |
[64]. |
|||
|
|||||
|
|||||
Л |
1 0 |
2 |
0 |
p |
|
|
|
|
|
|
|
Анализ установившихся свободных движений в релейноимпульсной экстремальной системе (РИЭС) сводится к исследованию условий существования предельного цикла, т е. автоколебаний системы вокруг положения экстремума. Рассмотрим метод определения условий существования предельного цикла в РИЭС, развитый в [48]. Введем понятие
~
преобразованного показателя экстремума [s, ] , под которым
148
~ |
~ |
в РИЭС с |
будем понимать [s, ] z[s, ] zmax |
||
~
запоминанием экстремума и [s, ] z[s, ] в РИЭС с
переключением по величине и знаку первой разности
показателя экстремума ~ в установившемся режиме. z[s, ]
Используя преобразованный показатель экстремума, условия переключения в РИЭС запишем в виде
|
~ |
|
|
|
|
N 1, 0 |
(2.68) |
|
|
N 1, , |
|||||||
Определим характеристику РИЭС |
M (N , ) : |
|
|
|||||
M (N , ) |
1 |
|
~ |
|
~ |
|
|
|
|
|
|
[N 1, |
] j [N 1, |
], |
(2.69) |
||
2 sin |
|
|
||||||
|
|
|
|
|
|
|
||
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где N — полупериод автоколебаний, содержащий целое число интервалов дискретности (N = kT).
С учетом этой характеристики условия переключения (2.68) примут вид
I |
m |
M (N, ) , |
Re M (N , ) 0. |
(2.70) |
|
|
|
|
Начертив M (N , ) на комплексной плоскости, легко
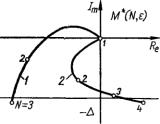
получим графическую интерпретацию условий переключения (2.70) (рис. 2.15). Чтобы периодический режим в РИЭС существовал, необходимо, чтобы точка пересечения
характеристики M (N , ) с прямой — лежала слева от
мнимой оси. Поэтому в РИЭС с характеристикой 1 периодический режим существует, а в РИЭС с характеристикой 2 — нет. Полупериод колебания N 0
определяется как ближайшая к прямой — точ-
ка на M (N , ) . для которой
M (N0 , ) лежит ниже прямой — .
Поэтому в РИЭС с характеристикой 1 (рис. 2.15) существует периодический режим N 0 =3.
С учетом этого правила построение
характеристики РИЭС можно Рис. 2.15. Характеристики производить для ε =1, т. е.
РИЭС. Разностный фазовый портрет релейноимпульсной экстремальной системы.
M (N ) |
1 |
|
~ |
~ |
|
|
|
|
|
[N ] j [N ] . |
(2.71) |
||
2 sin |
|
|
||||
|
|
|
|
|
||
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
Для определения характеристики M (N ) |
необходимо |
|||||
найти реакцию импульсной системы |
~ |
|
||||
z[s] с квадратичной |
||||||
нелинейностью на периодический дискретный входной сигнал
~
u[s] (рис. 2.9, 2.10) с помощью метода, изложенного в [16].
Для различных РИЭС в [48] приведены точные и приближенные формулы для M (N ) .
150
149
