Учебное пособие 2015

и выполнение условия (3.34), выражение (3.37) не отличается от (3.26). Уравнения динамики систем рис. 3.3, а и 3.3, 6 также не отличаются друг от друга при выполнении условий эквивалентности (3.34) и (3.38) и будут иметь вид

Реализация разомкнутых систем с компаундирующей связью по возмущению, близких к инвариантным, без потери устойчивости не вызывает никакого сомнения. Возникает вопрос, возможно ли реализовать дифференциальную систему, близкую к инвариантной, без непосредственной связи по возмущению (рис.3 .3, 6). Казалось бы, что в этой системе выполнение условия абсолютной инвариантности (3.33) неосуществимо не только по причине не идеальности дифференциаторов, но и приводит к потере устойчивости, так как само условие инвариантности предусматривает введение в

систему звена с бесконечным коэффициентом усиления. С другой стороны, выполнение основного условия эквивалентности (3.34) предусматривает связь не только по

имеющих связи по производным от регулируемой величины, возможно сохранение устойчивости при бесконечно больших коэффициентах усиления (если в системе нет звеньев с постоянным запаздыванием). Поэтому рассматриваемую

252

систему, если m p m0 m1 p m2 p2 ..., т. е. при идеальных производных, можно было бы настроить так, чтобы она была, абсолютно инвариантна к возмущению t и не теряла при этом устойчивости.

Пример. Пусть

Решив уравнения динамики элементов системы относительно и с учетом (3.40), получим

p 1 p a3a4n p a1a2a3a4k m0 m1 p m2 p2 (3.41)p a3a4n p .

Отсюда условием абсолютной .инвариантности будет

Предположим, что условие абсолютной инвариантности выполняется неточно, т. е.

Подставив это выражение в уравнение динамики систе-

253

где

a0 1 km2 ; a1 1 km1;

a2 km0 ;

q a1 ; 2a0

b1 1 .

Из этого решения видно, что, изменяя коэффициент , можно

изменять не только форму переходного процесса, но и его знак, т. е. знак динамической ошибки. Это подтверждает, что в рассматриваемой системе при допущении возможности получения идеальных производных можно добиться не только полной компенсации, но и перекомпенсации динамической ошибки. Другими словами, в многоконтурной системе без связи по возмущению можно получить при наличии идеальных производных не только абсолютную инвариантность, но и отрицательную динамическую ошибку. Под идеальной отрицательной динамической ошибкой понимается переходная ошибка, в которой фазы всех ее составляющих обратны по знаку фазам составляющих обычной положительной переходной ошибки.

В действительности ни один реальный дифференциатор не может быть идеальным, т. е. безинерционным. Поэтому рассмотрим систему, в которой используются реальные производные.

Пример. Пусть

255

Из (3.48) видно, что абсолютной инвариантности в системе получить невозможно. Если удовлетворить условие

то получим только систему с астатизмом второго порядка, так как коэффициент при второй производной в правой части уравнения, несмотря на свою малость (постоянная времени дифференциатора), все же не равен нулю.

Условиями устойчивости, по Гурвицу, для этой системы при a0 0 и a2 0 будут

m0k 1 2 0.

Отсюда можно определить значения коэффициентов m1

ипри которых система остается устойчивой.

1 3 ,

1 3

256

Введение связи по второй производной т отклонения с использованием реальных дифференциаторов не приводит к желаемому результату.

Действительно, уравнение динамики такой системы при равенстве постоянных времени всех дифференциаторов имеет вид

производной по отклонению не только не позволяет настроить систему на абсолютную инвариантность, но даже не повышает порядок ее астатизма, так как коэффициенты при первой и второй производных в правой части уравнения не могут одновременно быть равными нулю. Несмотря на это, система со связями по первой и второй производным от регулируемой величины имеет существенное преимущество перед системой со связью только по первой производной; заключается оно в том, что данная система обладает большим запасом устойчивости и позволяет варьировать коэффициент в

широких пределах. Тем самым обеспечивается настройка системы, близкой к ин-

вариантной, а также настройка на отрицательную динамическую ошибку без потери устойчивости.

В этой системе всякое изменение коэффициентов левой части уравнения динамики, вызванное изменением параметра, можно скомпенсировать каким-либо из коэффициентов

m0 , m1, m2 . Система была испытана на электронной аналоговой

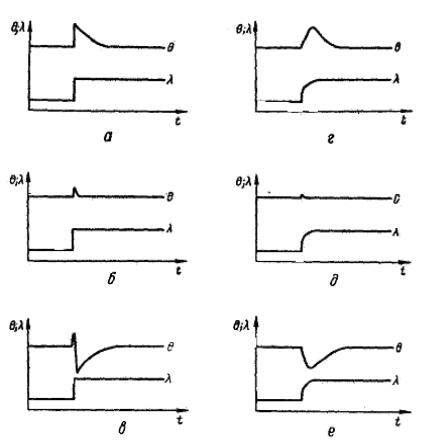
машине МН-7. Из осциллограмм, приведенных на рис. 3.4, а, б, в, видно, что абсолютной инвариантности получено не было. Несмотря на это, качество регулирования при введении связей n p и m p намного улучшается. причем изменение

коэффициентов и позволило получить

отрицательную динамическую ошибку (рис. 3.4, в) без нарушения устойчивости системы. Наличие кратковременного положительного всплеска в начале процесса можно объяснить невозможностью сведения к нулю коэффициента при второй и третьей производных в правой части уравнения динамики системы (рис. 3.5).

Очень жесткие требования, которые предъявляются к реальным дифференциаторам, часто бывают неоправданны, так как при их помощи невозможно получение идеальной производной и идеального скачка. Процессы, которые происходят в реальных объектах регулирования, обычно достаточно инерционны, и в сравнении с инерцией этих процессов инерция реального дифференциатора исчезающе мала. действительно, если на входе объекта регулирования действует возмущение , изменяющиеся не скачком, а по экспоненте с незначительной постоянной времени, то в рассматриваемой системе можно получить как полное устранение ошибки, так и чистую от-

258

рицательную динамическую ошибку без потери устойчивости. На рис. 3.4.г,д,в, приведены осциллограммы переходных процессов, подтверждающие это.

Рис.3.4. Осциллограммы переходных процессов в инвариантных системах:

259

а, б, в — при скачкообразном возмущении; г, д , е —при экспоненциальном возмущении.

Таким образом, несмотря на то, что в принципе как в разомкнутых системах со связью по возмущению так и в замкнутых многоконтурных дифференциальных системах без непосредственной связи по возмущению невозможно

может свести к нулю статическую и динамическую ошибки без потери устойчивости системы.

Пример. Одним из примеров практического применения дифференциальных систем экстремального управления может служить автоматическая очистка воды на тепловых электростанциях. Процесс получения водяного пара высокой температуры и давления характерен тем, что создаются условия. при которых отдельные примеси. содержащиеся даже в самом незначительном количестве в питательной воде, могут приводить котельные агрегаты к аварийному состоянию и длительному выходу их из строя. Поэтому питательная вода должна содержать минимальное количество вредных для котла и турбины примесей.

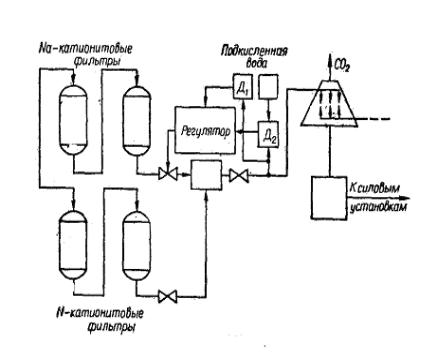
Известным методом химической очистки исходной воды является параллельное H-Na катионирование. Пропуская часть обрабатываемой

Рис.3.5. Применение дифференциальной системы экстремального управления для оптимального управления процессом химической очистки воды на тепловых электростанциях.

воды через H-катионитовые, а часть через Na-катионитовые фильтры и регулируя в зависимости от характеристик сырой воды соотношение этих потоков при их смешивании, можно получить в результате умягченную воду с желаемой величии

261

ной остаточной щелочности (рис.3.5). Было замечено, что электрическое сопротивление воды максимально тогда, когда вода имеет нейтральную реакцию. Учитывая технологические особенности эксплуатации паросиловых установок, необходимо подготавливать питательную воду со слабощелочной реакцией. Если показ качества взять электрическое сопротивление, то нужно создать такую систему регулирования, которая удерживала бы рабочую точку объекта на некотором удалении от экстремума.

Таким образом, сама постановка задачи в рассматриваемом примере подсказывает целесообразность применения одного из вариантов дифференциального экстремального регулятора с моделями нелинейной части объекта регулирования.

Для химочистки воды легко создать мо объекта регулирования. В данном случае объект регулирования можно представить в виде двух звеньев: линейного инерционного звена (смесителя) и нелинейного безынерционного звена (датчика сопротивления). Можно без особых затруднений подсоединить к смесителю несколько датчиков сопротивления. Каждый датчик будет служить моделью нелинейной безынерционной части объекта регулирования, так как экстремальная характеристика формируется в самом датчике. Чтобы получить сдвиг характеристик датчиков, необходимо в один из них подавать определенную дозу заранее подкисленной H-катионированной воды. При этом экстремальная характеристика R f k

сопротивление воды;

Рис.3.6. Применение дифференциальной системы экстремального управления при настройке следящей системы.

К—положения регулирующего органа при полностью открытом клапане — К = 100%) этого датчика переместится в сторону увеличения регулирующего воздействия в соответствии с дозой и концентрацией добавляемой подкисленной воды.

При условии идентичности датчиков их характеристики

263

пересекаются только в одной точке, и, не допуская — большой ошибки, можно считать, что их характеристики эквидистантны.

Разность сопротивлений датчиков меняет знак в точке пересечения этих характеристик. Местонахождение точки пересечения относительно экстремума зависит только от величины и знака постоянного смещения. При дрейфе характеристики первого датчика, происходящего в результате изменения состава исходной воды, характеристика второго датчика перемещается, не меняя своего положения относительно первого датчика. Основ на этих свойствах характер датчиков, можно при помощи дифференциального регулятора. удерживать систему на определенном сдвиге от экстремума.. Такого рода система оптимального управления процессом химической очистки воды была испытана на многих теплоэлектростанциях.

Несмотря на очень непродолжительное время, прошедшее после того, как были предложены дифференциальные системы экстремального регулирования с моделями объекта, их преимущество по сравнению с обычными системами экстремального регулирования нашли широкое признание.

Кроме описанных объектов, к которым применима дифференциальная система экстремального регулирования с моделями, можно назвать еще некоторые совершенно отличные от описанных выше, производственные объекты.

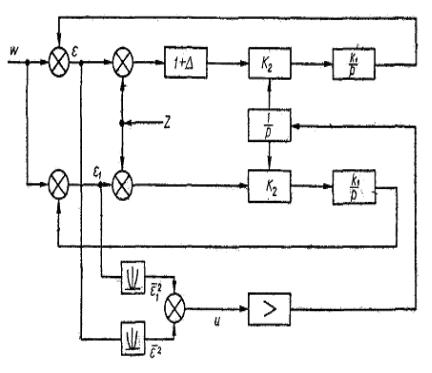
На Международном конгрессе ИФАК Ф. Меш сделал

доклад, в котором рассматривается следящая система (рис.3.6). Рассмотрим эту систему подробнее. Пусть на систему действует полезный сигнал W, имеющий спектральную

264

параметры k,n и коэффициент усиления K1 непрерывно изменяются. Задача состоит в отыскании оптимального значения коэффициента усиления K2 , причем в качестве

критерия оптимальности принимается среднеквадратичная ошибка управления (интегральный квадратичный критерий качества регулирования)

Это среднеквадратичное значение можно вычислить по спектральной плотности погрешности управления s :

Предполагается, что входные воздействия стационарны, а параметры систем изменяются очень медленно, для регулирования, применяя известные методы, можно получить

Эта функция имеет минимум при K 1n , но так как n и

265

K1 — величины переменные, то невозможно выбрать наперед заданное постоянное значение K2 для того, чтобы система всегда работала в минимуме функции.

В данном случае сама собой напрашивается идея автоматического поиска этого минимума при помощи изменения K2 , Эту задачу можно решить при помощи любой поисковой системы экстремального управления.

Нетрудно заметить, что именно здесь наиболее целесообразно применить описанную дифференциальную систему экстремального управления без поисковых колебаний. Как уже указывалось, идея дифференциальных систем состоит в том, что вместо измерений показателя экстремума последовательно во времени два раза, измерение одновременно проводится в двух точках пространства.

Как видно из рис.3.6, построение дифференциальной системы в данном случае не вызывает принципиальных затруднений. для решения этой задачи достаточно создать вторую идентичную следящую систему с последовательно включенным звеном, передаточный коэффициент которого должен быть равен 1 . . Это вызовет незначительное

рассогласование коэффициентов K2 в обеих системах, так как в дополнительной системе (модели) общий коэффициент усиления соответствующей цепочки будет равен K2 1 .. В

результате этого экстремальные характеристики на выходе квадраторов сместят относительно друг друга.

Действие такой системы ничем не отличается от действия уже рассмотренных ранее систем.

266

3.2. Экстремальные беспоисковые системы с корреляторами.

Статистические (и в первую очередь корреляционные) методы применяются для решения широкого круга задач автоматического управления — от определения динамических характеристик систем автоматического управления до автоматического измерения скорости движущихся объектов и расстояния до них. В самонастраивающихся системах (СНС) корреляторы используются как формирователи некоторого статистического показателя (автокорреляционной или взаимной корреляционной функции входных сигналов), который затем оптимизируется с помощью системы экстремального регулирования.

СНС с коррелятора могут быть условно разделены на две группы:

1)СНС, в которых определяются и оптимизируются динамические характеристики системы (коррекция параметров СНС в соответствии с изменением условий работы);

2)корреляционные измерительные системы с автоматической оптимизацией (корреляционные измерительные экстремальные системы).

В системах первой группы с помощью коррелятора формируется некоторый показатель, косвенно связанный с динамическими свойствами системы, который затем оптимизируется. Ряд систем этой группы описан в работах

[22,34, 35].

Системы второй группы являются взаимно корреляционными измерителями временных интервалов (относительного временного сдвига двух сигналов). В этих

267

СНС вычисляется взаимная корреляционная функция двух сигналов и отслеживается перемещение ее максимума вдоль оси абсцисс. Процесс слежения за максимумом осуществляется с помощью беспоисковых схем экстремального регулирования (дифференциальных и др,) [11]. Эти системы практически применяются для бесконтактного измерения скорости движения, направления на движущийся объект, расстояния до него и его положения. Ниже будут рассмотрены СНС с корреляторами, относящиеся ко второй группе.

При измерении расстояния корреляционным методом измеряется временной сдвиг между зондирующим и отраженным сигналами [27, 39, 41] или уровень взаимной корреляционной функции зондирующего и отраженного сигналов при фиксированном значении задержки зондирующего сигнала [ 14, 40 ].

При измерении направления на движущийся объект (его угловых координат) корреляционным методом определяется расстояние от объекта до двух разнесенных на фиксированное расстояние приемников, после чего по трем известным сторонам треугольника определяются углы последнего и угловые координаты объекта.

При измерении скорости движения корреляционным методом измеряется временной сдвиг сигналов, снимаемых с двух точек движущейся поверхности, расположенных по направлению движения [11].

Во всех приведенных выше случаях вычисляется взаимная корреляционная функция рассматриваемых сигналов и отслеживается положение проекций ее максимума на ось абсцисс, т. е. все эти задачи сводятся к измерению временных интервалов корреляционными методами. Автоматизация процес-

268

са слежения за максимумом корреляционной функции наиболее просто осуществляется с помощью беспоисковой дифференциальной схемы экстремального регулирования [ 7, 12, 13]. Положительным свойством корреляционных измерителей является очень высокая точность (методическая погрешность измерения не превышает долей процента) и отсутствие непосредственного контакта с движущимся объектом.

Автоматические корреляционные методы измерения параметров движения применимы также в навигации при определении положения движущихся объектов путем совмещения двумерной карты местности с изображением последней на экране радиолокатора. 3адачи в этом случае сводится к формированию пространственного показателя качества (двумерной корреляционной функции) и отыскания его экстремума [36]. Данная задача является одним из этапов более общей задачи распознавания образов корреляционными методами.

В последние годы за рубежом интенсивно разрабатываются корреляционные методы измерения параметров движения, что объясняется в первую очередь перспективностью этих методов для решения задач гидролокации, радиолокация, авиационной и космической навигации (слежение за спутниками и космическими кораблями, измерение скорости для мягкой посадки на Луну и т. д.) [ 1, 19, 23. 29, 37].

Поскольку все автоматические корреляционные методы измерения параметров движения (скорости, расстояния, угловых координат в положения) используют автоматическое слежение за максимумом корреляционной функции, в качестве области применения этих методов будет рассматриваться наиболее простая задача измерения скорости движения.

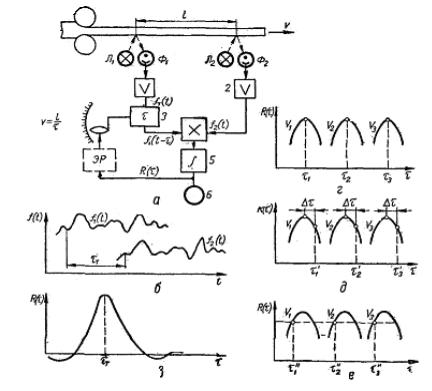
269

Ниже приводится пример измерения скорости движения прокатываемого металла. Описываемые методы и схемы применимы также для автоматического измерения скорости движения любых поверхностей и сред, являющихся носителями информации (т. е. поверхностей и сред, различные участки которых характеризуются какими-либо показателями, изменяющимися в направлении движения — геометрическими, оптическими, электрическими, магнитными и т. д.). Физический характер носителя информации не имеет принципиального значения — важно лишь, чтобы последняя могла быть воспринята каким-либо датчиком.

1. Корреляционный метод измерения скорости движения

Блок-схема корреляционного измерителя скорости движения проката (КИСП) приведена на рис.3.7, а. На поверхность металла, движущегося со скоростью , проектируются изображения нитей двух осветителей Л1 и Л2 , находящихся на фиксированном расстоянии l друг от друга. Фотодатчики Ф1 и Ф2 воспринимают переменную яркость изображений,

обусловленную неравномерной поверхностной структурой металла. Случайные сигналы с выхода фотодатчиков (рис. 3.7, 6) усиливаются усилителями 1 и 2 и подаются на коррелятор. состоящий из блока регулируемого запаздывания 3, множительного устройства 4 и интегратора (или сглаживающего фильтра) 5, к выходу которого подключен измерительный прибор 6. Входные сигналы коррелятора подобны по форме, но сигнал второго фотодатчика отстает во времени на величину транспортного запаздывания

270

Рис.3.7. Взаимно корреляционный метод измерения скорости движения.

представляющей собой текущее значение взаимной корреляционной функции входных сигналов

271