
Учебное пособие 2015
.pdf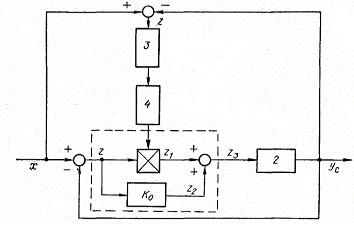
n
cмi yм(i)
i 0
K y K0 |
K1 ; |
|
|
||
|
|
||||
|
|
|
|
|
|
K y K0 |
K1 |
|
|
|
|
Ku 1dt; |
- |
||||
K y K0 |
Ku |
|
1dt |
|
|
|
|
||||
|
|
|
|||
рассматриваемые уравнения цепи самонастройки;
x — модель,
где у, ум, z, ε - выходные координаты соответственно объекта управления, модели, управляющего устройства и цепи самонастройки;
х- входная координата системы; z=x-y;
ε1 = |ум| - |у| - сигналы рассогласования соответственно системы и координат модели и системы;
Kу - коэффициент усиления управляющего устройства;
ci(t), b(t) - переменные коэффициенты уравнения объекта управления;
cмi - постоянные коэффициенты уравнения модели; Ки, К - постоянные коэффициенты.
1.6. 3. Исследование динамики самонастраивающейся системы с эталонной моделью при детерминированных
сигналах методом гармонической линеаризации
Основные допущения. С известным приближением оказывается возможным при медленном изменении параметров объекта управления считать их фиксированными, а среди нелинейностей системы учитывать лишь нелинейность, создаваемую за счет множительного и логического устройств контура самонастройки.
Рис. 1.10. Структурная схема СНС с идеальной моделью.
С такими допущениями можно оценить влияние структуры и параметров цепи самонастройки на устойчивость системы и качество самонастройки, на переходный процесс системы, ее установившуюся погрешность, на возможность возникновения автоколебаний.
Исследование СНС может проводиться методом фазовой плоскости, методом гармонической линеаризации и др. При определенных упрощениях методом фазовой плоскости могут исследоваться многие практические системы управления разного рода объектами, описываемые уравнениями не выше второго порядка.. Большими возможностями обладает метод гармонической линеаризации, применение которого рассматривается ниже.
53
52
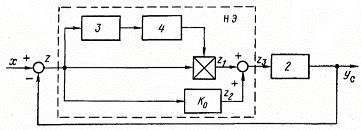
Рис. 1.11. Преобразованная структурная схема СНС с моделью:
НЭ— нелинейный элемент системы. Исследование устойчивости СНС с идеальной
моделью (рис. 1.10). Передаточная функция линейной части системы имеет вид
K ( p) |
c |
m |
p m c |
m 1 |
p m 1 .. c p c |
0 |
|
||||
|
|
|
1 |
|
. |
||||||
d |
n |
pn d |
n 1 |
pn 1 .. d |
1 |
p d |
0 |
||||
|
|
||||||||||
|
|
|
|
|
|
|
|||||
Для удобства анализа схему 1.10 преобразуем к виду, показанному на рис. 1.11. Гармонический коэффициент преобразования нелинейного элемента относительно 1-й гармоники определяется выражением
K ( A, ) |
1 |
2 z |
|
sin d |
1 |
2 z |
|
cos d , |
|
|
|
|
|||||
1 |
A |
3 |
|
A |
3 |
|
||
|
|
|
|
|
|
|||
|
0 |
|
|
0 |
|
|
||
где z3 - сигнал на выходе НЭ;
А и ω - амплитуда и частота гармонического сигнала
z=
= А sinψ (ψ = ωt) на входе НЭ.
Искомые величины А и ω находятся на основании уравнения гармонического баланса
K(jω)K1(A, ω)= -1
Полагая в характеристическом уравнении замкнутой системы
dn pn dn 1 pn 1 .. d1 p d0 K1 (A, )cm pm
K1(A, )cm 1 pm 1 .. K1 (A, )c1 p K1 (A, )c0 0 p=jω преобразуем к виду
X(A, ω)+jY(A, ω) = 0.
Из совместного решения уравнений
Х(А, ω)=0; Y(A, ω)=0.
находим А и ω.
Возможность автоколебательного режима целесообразно определять, используя критерий Гурвица, согласно которому для такого режима требуется, чтобы при небольших вариациях найденной величины А, т. е. а А, условие Гурвица выполнялось при а>A и не выполнялось при а<А.
54 |
55 |
|
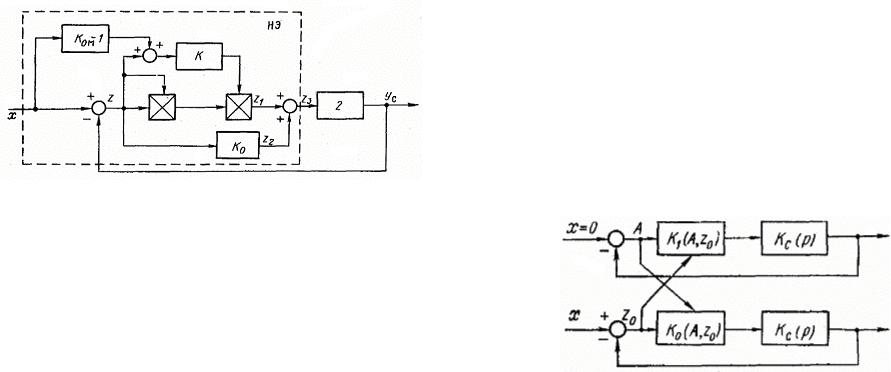
Рис. 1.12. Структурная схема СНС с преобразованным нелинейным элементом.
Если автоколебания в системе невозможны, то найденное значение А будет соответствовать границе устойчивости при заданных параметрах системы, т. е. выражение для А устанавливает связь параметров системы, цепи настройки и входных воздействий с условиями устойчивости.
Исследование устойчивости СНС с неидеальной моделью. Если на входе СНС действует медленно меняющийся (либо постоянный) сигнал, то эталонную модель можно представить в виде усилительного звена с коэффициентом усиления меньше единицы. Структурная схема исследуемой системы с Kц.н(р)=K приведена на рис. 1.12, Здесь
z |
3 |
z3 K z 2 xK(K |
0 м |
1) zK |
0 |
. |
(1.29) |
|
|
|
|
|
При постоянном сигнале x=x0 = const на входе системы автоколебания следует искать в виде
z z |
0 |
z* , |
(11.30) |
|
|
|
где z0 — постоянная составляющая;
56
z*=Asinψ и ψ =ωt
Учитывая выражения (1.29), (1.30) и равенство
|
1 |
|
2 |
|
|
K0(A)= |
|
|
z3 d , |
||
|
|
||||
2 z |
0 |
||||
|
|
||||
|
|
0 |
|
определим коэффициенты преобразования нелинейного элемента по постоянной составляющей К0(А) и по первой гармонике K1(A).
Рис. 1.13. Взаимосвязанные системы.
В результате исходная система разбивается на две взаимосвязанные системы (по постоянному и переменному сигналам), как это показано на рис. 1.13. Одна система характеризует автоколебательный режим, а другая — постоянную составляющую
K ( p)K |
( A, z |
0 |
) 1; |
|
|
|
||||||
1 |
|
|
|
|
|
|
(1.31) |
|||||
z0 xK z ( p) |
|
|
|
, |
|
|||||||
|
|
|
|
|
|
|
||||||
где |
|
|
|
p 0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
K z ( p) |
|
p 0 |
|
|
|
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
|
1 K0 |
( A, z0 )K ( p) |
|
p 0 |
||||||||
|
|
|
|
|||||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
57 |
|
|
|
|
|
Решая систему уравнений (1.31) с учетом ранее найденных значений Ко(А, z0) и K1(A, z0), находим предельно допустимое значение амплитуды входного сигнала, исходя из условий устойчивости при заданных параметрах СНС. В некоторых случаях определение граничного значения амплитуды входного сигнала при различных значениях Kом возможно на основе упрощенной методики. Предполагается, что СНС с неидеальной моделью (Kом 1) теряет устойчивость при достижении амплитуды сигнала на выходе нелинейного элемента того же значения, что и для идеальной модели (Kом =1), которое нетрудно определить. Для случая (1.29) уравнение относительно неизвестного сигнала будет иметь вид
[(K0M-1)x+x]Kx2+K0x=z3,
где z3 — сигнал на выходе НЭ системы с идеальной
моделью. |
|
|
|
|
Исследование |
СНС |
в |
режиме |
вынужденных |
колебаний. На систему (см. рис. 1.10) действует гармонический сигнал
x=Bsinωв t,
и вынужденные колебания для переменного значения z имеют вид
z =Aвsin(ωвt+θ), |
(1.32) |
где искомыми величинами являются амплитуда вынужденных колебаний Aв и фазовый сдвиг θ.
Для решения задачи х выражается через z, т. е.
х= В sin ωв t = В sin [(ωвt+θ) - θ]= В cos θ sin (ωвt+θ) – - В sin θ cos (ωвt+θ)
На основании выражения (1.32) и его производной
получим соотношения: |
|
|
|
|
|
|
|
|
|
|
sin(ωвt+θ) = |
|
z |
|
; |
|
|||
|
|
Aв |
|||||||
|
|
|
|
|
|
|
|
||
cos(ωвt+θ) = |
|
|
pz |
|
, |
||||
|
|
|
|||||||
|
A |
|
|||||||
|
|
|
|
|
|
в |
в |
||
следовательно, |
|
|
|
|
|
|
|
|
|
B cos |
|
B sin |
|
|
|||||
x= |
|
|
|
|
|
|
|
p z. |
|
|
|
|
|
|
|
||||
|
Aв |
|
Aв в |
|
|
||||
|
|
|
|
||||||
Значение х подставляем в уравнение динамики системы,
составленное относительно сигнала ошибки: |
|
z = x - zK1(A)K(p) |
(1.33) |
Для отыскания периодического решения с частотой ωв в характеристическое уравнение (1.33) подставим мнимое значение р=jω и выделим вещественную X и мнимую У части уравнения:
X 0; |
(1.34) |
|
Y 0. |
|
|
|
|
|
Уравнение, связывающее амплитуду вынужденных колебаний Aв с параметрами СНС, получим путем решения уравнений (1.34) относительно sinθ и cosθ и суммирования квадратов левых и правых частей полученных равенств.
Анализ полученного уравнения удобнее осуществлять, решая его относительно представляющего интерес параметра цепи настройки.
1.6.4. Статистическое исследование СНС с эталонной
58
59
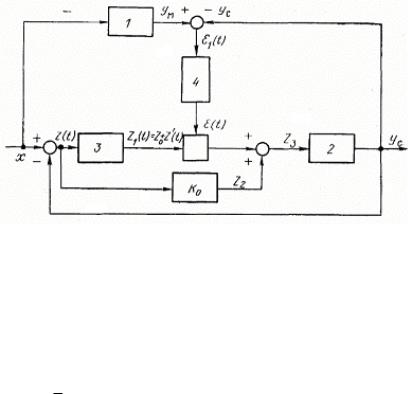
моделью
Статистическое исследование при нулевом математическом ожидании. Структурная схема исследуемой системы приведена на рис. 1.14, где в качестве логического устройства используется квадратор, расположенный в прямой цепи сигнала ошибки системы.
Рис. 1.14. Структурная схема СНС с логическим элементом в
прямой цепи сигнала ошибки.
Выход квадратора (логического устройства) при воздействии на систему и модель даже центрированного случайного сигнала будет состоять из математического ожидания от квадрата сигнала ошибки подстраиваемой системы Z 2 =Z0 и его переменной составляющей Z' (t), т. е.
Z1(t)=Z0+ Z' (t).
Учет фильтрующих свойств системы позволяет предположить, что на выходе множительного звена действует лишь сигнал
Z1(t)ε(t) Z0 ε(t).
При этом структурная схема исследуемой системы преобразуется путем линеаризации к виду, показанному на рис. 1.15.
Флуктуационная ошибка в линеаризованной системе определяется путем совместного решения двух уравнений:
|
1 |
|
|
|
|
|
|
|
|
||
y2 |
|
|
S f |
( ) |
Kол ( j , Z0 ) |
2 d |
|
||||
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
(1.35) |
|||
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
||||
Z0 |
|
|
|
|
S f |
( ) |
Kzл ( j , Z0 ) |
d |
|
|
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
где Kол(р, Z0) и Kzл(р, Z0) - соответственно передаточные функ-
ции системы и ошибки;
Sf (ω) - спектральная плотность входного сигнала;
ζу2 - дисперсия флуктуационной ошибки.
При заданных параметрах системы из второго уравнения (1.35) находится величина Z0, после подстановки которой в первое уравнение определяется значение ζу2.
61
60
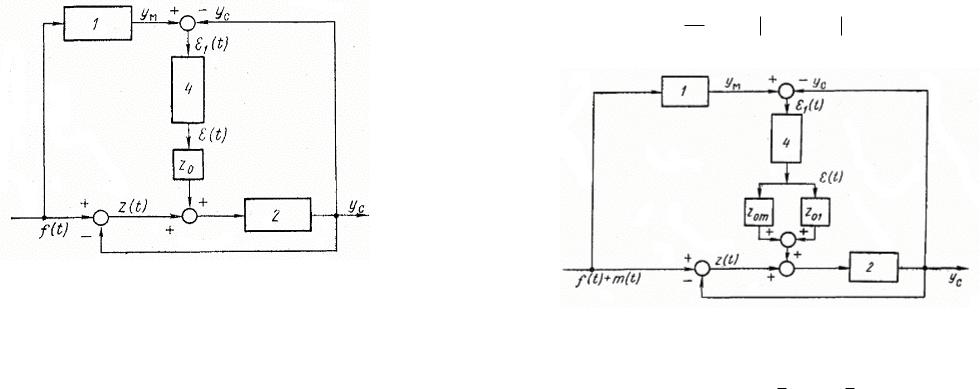
Рис. 1.15. Линеаризованная схема СНС.
Статистическое исследование при ненулевом математическом ожидании случайного воздействия на входе СНС. Структурная схема линеаризованной системы приведена на рис. 1.16, где ненулевое математическое ожидание m(t) представляет собой полезный сигнал. При постоянном полезном сигнале величина Z0m определяется выражением
Z0m={lim pm( p)K zл ( p, Z0 )}2 ,
p 0
а величина Z01 |
находится с |
помощью интегрального |
|||||||||||
соотношения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
S ( ) |
|
K |
|
( j, Z |
|
) |
|
2 d ; |
|
|
|
|
|
|
|||||||||
|
2 |
|
|
||||||||||
|
01 |
|
|
f |
|
|
zл |
|
0 |
|
|
|
|
ζ 2 = 1 S ( ) K ( j , Z ) d , у 2 f ол 0
Рис. 1.16. Линеаризованная схема СНС при ненулевом математическом ожидании,
где
Z0=Z0M+Z01; Z0M= Z m 2 ; Z01= Z12 ;
Z1 — высокочастотная составляющая сигнала на входе логического устройства;
Zm — его математическое ожидание.
1.6.5. Пример анализа динамических свойств беспоисковой СНС с эталонной моделью
Объект управления, модель и цепь настройки описываются передаточными функциями:
63
62

K(p) = |
|
|
Kc |
|
|
; |
1 2 T p T 2 p 2 |
||||||
|
|
|
c c |
c |
|
|
K0M(p) = |
K M |
; |
|
|
||
1 TM p |
|
|
||||
Kц.н(p) = |
K (1 T1 p) |
, |
|
|||
|
p |
|
|
|||
|
|
|
|
|
|
|
а логическое устройство в прямой цепи сигнала ошибки выполнено на квадраторе.
Требуется оценить устойчивость и определить флуктуационную ошибку при воздействии на систему помехи со спектральной плотностью
Sf(ω) = |
N0 |
, |
1 2 2 |
где N0=0.1 в2*сек; α = 0,01 сек. |
|
|
|
|
||||||
Параметры СНС имеют следующие значения: K0=1; Kс = |
||||||||||
10; K = 10 сек-1; ξ = 0.1, Tс = 1 сек; T1 = 1.5 сек; Tм |
= 0,5 сек; |
|||||||||
Kм = 0.5. |
|
|
|
|
|
|
|
|
|
|
1. Предварительное исследование устойчивости для |
||||||||||
случая идеальной модели (К0м (р) = 1). |
|
|
|
|||||||
Характеристическое |
уравнение исследуемой |
системы |
||||||||
равно |
|
|
|
|
|
|
|
|
|
|
p 2T 2 p * 2 |
T K |
c |
K |
( A,) 1 0, |
(1.36) |
|||||
c |
|
c c |
|
1 |
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
K |
( A, ) K |
|
A2 |
* 0.75KT |
A2 K |
. |
|
|||
0 |
|
|
||||||||
1 |
|
|
|
|
|
1 |
4 |
|
||
|
|
|
|
|
|
|
|
|
||
Преобразование уравнения (1.36) к виду
X + jY = 0
дает:
64
X 1 K K |
|
|
A2 * 0.75KK T 2T 2 |
0; |
||||||||||||
|
0 |
c |
|
|
|
|
|
|
|
c |
1 |
|
c |
|
||
|
|
|
|
|
|
A |
2 |
KK c |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Y * 2 cTc |
|
|
|
0. |
|
|
|
|
||||||||
|
|
4 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.37) |
На основании решения уравнений (1.37) находим: |
|
|||||||||||||||
2 |
1 K |
0 |
K |
c |
|
A2 * 0.75KK T |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
c |
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
T 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
8c (1 K 0 K c ) |
. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
KK |
c |
(T 6 T ) |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
c |
c 1 |
|
|
|
|
||
Исследование уравнения (1.36) показывает, что автоколебательный режим в системе невозможен, а система может потерять устойчивость при входном сигнале x = 0,936 в.
2. Для статистического исследования исходная система линеаризуется, в результате чего передаточные функции линеаризованной системы и ошибки в общем случае имеют вид:
K л ( p, Z0 ) K0M ( p)Kц.н ( p)Z0 1 K ( p) ; 1 K ( p) K ( p)Kц.н ( p)Z0
K z ( p, Z 0 ) 1 K л ( p, Z 0 )
С учетом заданных параметров передаточные функции системы и ошибки соответственно равны:
65

K л |
(p, Z0 ) |
|
|
|
|
|
|
|
5p 2 (10 75Z |
0 |
)p 50Z |
0 |
|
|
|
|
|
|
; |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0.5p4 1.1p3 |
(10.7 150Z |
0 |
)p2 (11 250Z |
0 |
)p 100Z |
0 |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
(1.38) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(p, Z0 ) |
|
0.5p4 1.1p3 (5.7 150Z )p2 |
(1 175Z |
0 |
)p 50Z |
0 |
|
|
||||||||||||||||
K zл |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
. |
|||
|
0.5p4 |
1.1p3 |
(10.7 150Z )p2 |
(11 250Z |
)p 100Z |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.39) |
|
|||
Усредненное |
значение сигнала |
|
|
ошибки |
Z0 в |
|
|||||||||||||||||||
соответствии с уравнением (1.39) для заданного входного |
|
||||||||||||||||||||||||
воздействия равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Z0= |
1 |
|
|
Kzл (j , Z0 ) |
|
2 S f |
( )d . |
|
|
|
|
(1.40) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
После преобразования выражения (1.40) получим
Z03 + 7.77Z02 - 1.55Z0-0.0059 = 0.
Из решения этих уравнений находим Z0 = 8,l в2. Величина флуктуационной ошибки СНС определяется с
учетом выражения (1.38) и значения Z0:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
(j , Z ) |
|
2 S |
|
( )d 0.236в. |
|
|
|
K |
|
|
|
|||||||
|
2 |
|
|
|||||||||
|
л |
|
|
zл |
0 |
|
|
f |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Флуктуационная ошибка для эталонной модели м=0,157 в и системы без учета самонастройки с = 1,52 в.
Процесс нахождения флуктуационной ошибки в СНС можно упростить, если в качестве величины Z0 использовать значение Z0м, найденное для эталонной модели. Такое допущение справедливо при близости динамических свойств СНС и динамических свойств модели.
66
Для данного примера величина дисперсии ошибки эталонной модели
Z0м = 21 K zм (j ) 2 S f ( )d 5в 2 .
Величина флуктуационной ошибки СНС, найденная при использовании Z0м, равна
ζл = 0,242 в.
Приведенное упрощение позволяет облегчить задачу определения влияния структуры и параметров цепи настройки на динамику СНС.
1.7. Синтез самонастраивающихся систем с эталонной моделью вторым методом ляпунова
При построении беспоисковых СНС с эталонной моделью прежде всего должна быть решена задача выбора управляющих устройств, обеспечивающих их устойчивость. Указанная задача вследствие нелинейности и нестационарности системы сложна, однако она достаточно успешно решается на основе второго метода Ляпунова, который является одним из наиболее строгих методов анализа и синтеза нелинейных систем управления. Его применение позволяет синтезировать из условия устойчивости СНС с эталонной моделью и различными видами настроек.
1.7.1Синтез СНС с эталонной моделью и сигнальной
настройкой
Задача синтеза в этом случае сводится к определению структуры и параметров управляющего устройства,
67
гарантирующего устойчивое движение объекта относительно движения модели без перестройки его параметров. При этом часто возникает необходимость учета ограничений управляющего воздействия. С этой целью в уравнение обобщенного объекта, включающего все инерционности основной системы, вводится нелинейная функция с насыщением Ф(g):
n 1 |
|
y (n) ai (t) y (i) k(t)Ф(g), |
|
i 1 |
(1.41) |
где ai(t), k(t) — переменные во времени коэффициенты; g — сигнал управления;
Ф(g) — функция, удовлетворяющая условию:
Ф(g) = 0 при g =0 ; gФ(g)>0 при g≠0 ; Ф(g)=M при g = C.
В качестве эталонной модели принимается звено, в общем случае описываемое уравнением вида
n 1 |
|
yм(n) bi yм(i) |
k м x, |
i 0 |
(1.42) |
где х — ступенчатый входной сигнал.
Построение самонастраивающейся системы производится в следующей последовательности. В соответствии с выражениями (1.41) и (1.42), введя обозначения
ε(i) = yм(i) – y(i) |
(i =0, 1, …, n), |
(1.43) |
составляем уравнение для ошибки: |
|
|
n 1 |
n 1 |
|
(n) bi (i) ai (t) bi y (i) |
k м x k(t)Ф(g). |
|
i 0 |
i 0 |
(1.44) |
С целью упрощения математических выкладок равенстве (1.44) представляем в матричной форме:
x Ax u ; |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0 |
|
|||||
|
x1 |
|
|
|
|
0 |
|
|
0 |
0 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
||
x |
|
u |
|
|
|
0 |
0 |
0 |
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
b 0 |
b1 |
b 2 |
b n |
|
||
|
xn |
|
|
|
|
u0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, (1.45) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
. |
|||
|
|
|
u0 ai (t) bi y (i) k м x k(t)Ф(g) |
|
(1.46) |
||||||||||
i 0
Выбираем функцию Ляпунова в виде определенно положительной квадратичной формы фазовых координат:
V(x1, x2, …, xn; t) = x Px ,
где V(0,t) = 0;
x — транспонированный вектор; Р — симметричная матрица:
|
p11 |
p12 |
p1n |
|
P |
p21 |
p22 |
p2n |
. |
|
|
|
|
|
|
pn1 |
pn 2 |
pnn |
|
Пусть норма вектора |
x |
определяется евклидовой |
||
|
||||
длиной вектора |
|
|
|
|
69
68

|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
2 |
|
|
x |
|
xi2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
||
и V( x , t) при |
|
|
x |
|
|
|
. |
Можно найти такую |
||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|||||||||||
неуменьшающуюся скалярную функцию В( 
 x
x 
 ) с В(0)=0, что
) с В(0)=0, что
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
V( x , t)= |
x Px В( |
|
|
|
) при t>0. |
|
|
|
|
|
|
|
|||
Определим полную производную по времени функции |
|||||||||||||||
Ляпунова на основе уравнения (1.45): |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
V (x, t) x Px |
x Px |
x ( A P PA)x |
2x Pu. |
(1.47) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если А — неособая матрица, то справедливо равенство |
|||||||||||||||
|
A'P+PA = -Q. |
|
|
|
|
|
(1.48) |
|
|||||||
Матрицу Q целесообразно выбрать диагональной: |
|||||||||||||||
|
|
|
|
q11 |
0 |
|
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||
|
Q |
|
|
0 |
q22 |
|
0 |
|
|
|
|
|
(1.49) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
qnn |
|
|
|
|
|
|
||
С учетом формулы (1.48) выражение (1.47) |
|||||||||||||||
преобразуется к виду |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
V (x, t) x Qx 2x Pu. |
|
|||||||||
(1.50) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Второй член правой части равенства (1.50) в соответствии с формулами (1.45) и (1.46) имеет вид
70
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2x Pu 2 pn1x1 pn2 x2 ... pnn xn u0. |
|
|||||||
Если выбрать |
|
|
||||||
u0 |
hsign( pn1 x1 |
pn2 x2 ... pnn xn ) |
|
|||||
|
|
|
|
|
|
hsign (0≤ h ≤ ), |
(11.51) |
|
где |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
при |
0; |
|
|
|
|
|
|
|
при |
0; |
|
sign 0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при |
0, |
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
||||
2x Pu 0 |
|
|
|
|||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V (x, t) x Qx. |
|
|
||||||
Выражение (1.51) с учетом уравнения (1.45) |
||||||||
преобразуется к виду |
|
|
||||||
n1 |
|
|
|
|
|
|
|
|
ai (t) bi y (i) k м z k м y k(t)Ф(z ) |
|
|||||||
i 0 |
|
|
|
|
|
|
|
|
hsign( pn1 x1 pn2 x2 ... pnn xn ), |
(1.52) |
|||||||
|
|
|
|
|
|
|
|
|
где x=z+y; g=z+δ.
Знак полученного выражения будет определяться знаком функции Ф(z+δ), если
71
