Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 2015

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

3.99 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 174 5 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

n 1

Ф( z)

ai (t) bi

y (i)

k м y

k м z

i 0

k(t)

max

(1.53)

Если представить нелинейную функцию в виде

Ф(z+δ) =ε(z+δ) (z+δ),

то условие (1.52) можно записать в следующей форме:

n 1

ai (t) bi y (i )

k м y

k м z

i 0

;

k(t)

max

(1.54)

max

sign δ= sign( pn1 x1 pn2 x2

... pnn xn ) .

(1.55)

На основе выражений (1.54) и (1.55) находим алгоритм

сигнальной настройки

y(1)

y (n 1)

... B

n 1

}sign( pn1 x1 pn2 x2

... pnn xn ),

(1.56)

где

(t) b0

;

a1 (t) b1

k(t)

max

…;

Bn 1

an 1 (t) bn 1

; C0

k(t)

max

k(t)

max

Для обеспечения непрерывного решения функцию знака в выражении (1.56) следует заменить функцией насыщения:

k1 0;

при

sat(k1 )

при

k1 0;

(1.57)

y(1)

y (n 1)

... B

n 1

}sat k1 ( pn1 x1

pn2 x2

... pnn xn ) .

(1.58)

учетом

ранее

введенных

обозначений (1.43)

алгоритм (1.58) преобразуется к виду

y(1)

y (n 1)

... B

n 1

}sat k ( p

(1) ... p

(n 1) ) .

(1.59)

n1 1

nn n

Структурная схема самонастраивающейся системы с моделью сигнальной настройки представлена на рис. 1.17.

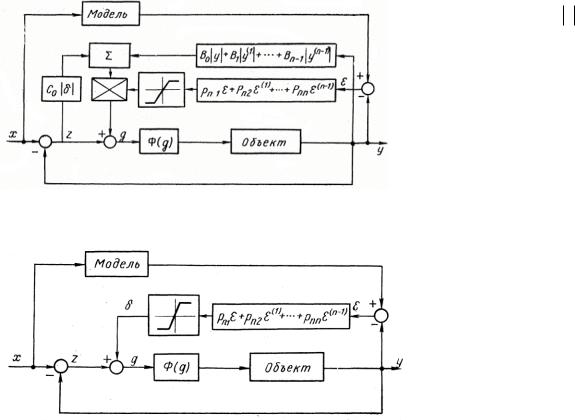
Рис. 1.17. Структурная схема СНС с моделью и сигнальной настройкой.

Рис. 1.18. Структурная схема СНС с моделью.
При	ограниченных	входных воздействиях	для
упрощения	практической	реализации СНС выражение,

стоящее в фигурных скобках неравенства (1.59), целесообразно заменить усилительным звеном:

y(1)

... B

n 1

y(n 1)

max .

В этом случае структурная схема системы (рис. 1.18) и алгоритм настройки значительно упрощается:

k y sat k1 ( pn1 1 pn2 2 (1) ... pnn n (n 1) ) .

Пример 1.2. Движение объекта описывается уравнением с переменными коэффициентами

y(3) a2 (t) y(2) a1 (t) y(1) a0 (t) y kФ(g),

где

a2 min a2 (t) a2 max ; a1min a1 (t) a1max ; a0 min a0 (t) a0 max .

Эталонная модель представляет собой звено с постоянными параметрами:

yм(3) b2 yм(2) b1 yм(1) b0 yм kм x.

Необходимо определить алгоритм сигнальной настройки. Решение. Составим уравнение для ошибки:

		2			n 1		y (i) k м x kФ(g)
(3)		bi (i) ai (t) bi					y (i) k м x kФ(g)
		i 0			i 0
и запишем его в матричной форме
	x1		0	1	0	x1		0
	x1		0	1	0	x1		0
	x2		0	0	1	x2		0
	x3		b0	b1	b2	x3		u0
где
		n 1
u0 ai (t) bi y (i) k м x k(t)Ф(g)
		i 0					.

Выберем функцию Ляпунова:

V (x, t) xi pij x j

i, j 1

и определим ее производную по времени:

V (x,t) q11 x12 q22 x22 q33 x32 2( p31 x1 p32 x2 p33 x3 )u0

где q11,q22,q33 - элементы диагональной матрицы (1.48):

q11=2b0p31; q22=2(b1p32-p12); q33=2(b2p33-p12);

Количество полученных уравнений недостаточно для определения всех неизвестных. Поэтому можно выбрать

b0p31>0; b1p32-p12>0; b2p33-p12>0;

Алгоритм настройки записывается в виде

y(1)

y(2)

}sign( p

x p

x ),

или

y(1)

y(2)

}sat[k ( p p

(1) p (2) )],

где

q11		0	0		0	0	b0			p11	p12	p13
q11		0	0		0	0	b0			p11	p12	p13
0		q22	0		1	0		b1		p21	p22	p23
0		0	q33		0	1	b2			p31	p32	p33
	p11	p12	p13	0		1			0
	p11	p12	p13	0		1			0
	p21	p22	p23	0		0				.
	p31	p32	p33	b0		b1		b2

Из последнего выражения следует:

p11=b0p32+b1p31; p21=b2p31+b0p33; p22=b2p32+b1p33-b31.

произвольно значения некоторых параметров, в частности p31, р32 и р33, соблюдая условия положительности матриц Р и Q:

p11>0;

p21*p22 –p222>0;

p11(p22*p33 –p322 ) – p12(p21*p33 –p31p32 )+

p31(p21*p32

–p31p22)>0.

a0 max b0

;

a1max

;

k min

…;

a2 max b2

kм

;

k min

Как видно из выражения (1.53), при больших входных сигналах и широком диапазоне изменения коэффициента усиления системы возникает необходимость в его стабилизации. С этой целью могут быть использованы различные способы. Одним из наиболее эффективных

является построение СНС с эталонной моделью и комбинированной настройкой.

2. Синтез СНС с моделью и параметрической настройкой

Задача синтеза СНС, использующих параметрическую настройку, по существу сводится к определению алгоритмов изменения перестраиваемых коэффициентов ky и ci (i = 0, 1, ...

, п-1).

Для ее решения вторым методом Ляпунова записываем уравнение движения объекта с учетом перестраиваемых коэффициентов:

n 1
y(n) [ai (t) k(t)c1 ] k y k(t)x.
i 0	(1.60)

В соответствии с выражениями (1.42) и (1.60) составляем уравнение для ошибки:

(n) n 1 bi (i) kм k y k(t) x {bn 1 [an 1 (t)

i 0

k(t)cn 1 ]}y(n 1) bn 2 an 2 (t) k(t)cn 2 y(n 2)

... b0 a0 (t) k(t)c0 y

	n 1	x	n	y(n 1)	n 1	y(n 2)	...	1	y,	(1.61)
	n 1		n		n 1			1		(1.61)
где
n 1 kм k y k(t);

n bn 1 an 1 (t) k(t)cn 1 ;


1 b0 a0 (t) k(t)c0 .
1 b0 a0 (t) k(t)c0 .										(1.62)
										(1.62)

Уравнение							(1.61)			целесообразно							представить		в
матричной форме:
	x1							1		0			0	x1				0
					0
					0
					0			0		1			0
	x2				0			0		1			0	x2				0
	x2													x2				0
					0			0		0			1
	xn				0			0		0			1	xn				u0
	xn				b0		b1		b2			bn		xn				u0
где					b0		b1		b2			bn					(1.63)
																	(1.63)

u		0			n 1	x	n	y(n 1)			n 1	y(n 2)	...		1	y.
		0			n 1		n				n 1				1
Функция Ляпунова выбирается в виде квадратичной
определенно положительной формы:
								n 1
					) x Px i i 2 ,
V (x,					) x Px i i 2 ,
								i 1									(1.64)
					( 1 , 2 ,..., n 1 ) ;
где					( 1 , 2 ,..., n 1 ) ;
	Р - симметрическая матрица;
i			-	положительные постоянные.

Полная производная по времени от функции Ляпунова (1.64) в силу выражения (1.63) имеет вид

n 1

V (x, ) x ( A P PA)x 2x Pu 2 i i i .

i 1

Если A является неособой матрицей, т. е. соответствует устойчивой эталонной модели, то определенно отрицательной форме

x Qx x (A P PA)x

(1.65)

соответствует определенно положительная форма x Px .

Определяем производную от функции Ляпунова, которая с учетом равенства (1.65) имеет вид

)

(11.66)

V (x,

x Qx

2x Pu

i i

i .

Матрица Q в формуле (1.66) может быть выбрана диагональной [см. выражение (1.49)].

Из формулы (1.66) в силу равенства (1.63) следует

	n 1
2x Pu	2 i i i	2( pn1 x1 pn2 x2 ... pnn xn )
	i 1
n1 x n y(n1) n1 y(n2)			n1
n1 x n y(n1) n1 y(n2)			... 1 y 2 i i i .

Для обеспечения устойчивости движения основной системы относительно движения эталонной модели и устойчивости процессов настройки коэффициентов необходимо выполнить условие

2 i i i

(1.67)

2x Pu

Неравенство (1.67) удовлетворяется, если

( pn1 x1

pn2 x2 ... pnn xn ) y;

( pn1 x1

pn2 x2

... pnn xn ) y(1) ;

(1.68)

( p

x p

... p

) y(n1)

;

n1 1

( p

x p

... p

)x.

n 1

n1 1

Находим алгоритмы настройки коэффициентов из выражений (1.62) и (1.68) в предположении квазистационарного (скачкообразного) изменения параметров системы:

( p

(1) ... p

(n 1) )x;

k n1

( p

(1) ... p

(n1) ) y

n 2

k n

( p

(1) ... p

(n1) ) y.

n 2

k 1

(n1) ;

(1.69)

Значения pni (i = 1, 2, ... , n) в уравнениях (1.69) выбираются из условия обеспечения положительности матриц Р и

В соответствии с системой уравнений (1.69) определяем структуру самонастраивающейся системы с эталонной моделью и параметрической настройкой (рис. 1.19).

Для повышения точности самонастройки в алгоритмы на стройки можно ввести, помимо интегральных, релейные составляющие.

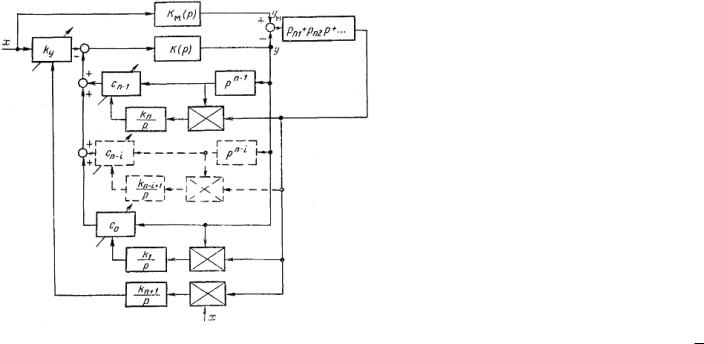
Рис. 1.19. Структурная схема СНС с моделью и параметрической настройкой.

Пример 1.3. Известны уравнения, описывающие движение объекта и модели:

y(3) a2 y(2) a1 y(1) a0 y k y k(t)x;

yм (3) b2 yм (2) b1 yм (1) b0 yм kм x,

где bi= ai , t=0, 1, 2.

Необходимо определить алгоритмы настройки из условия обеспечения равенства

ky k(t) kм

Решение. Для решения задачи составляется уравнение ошибки

(3) b2 (2) b1 (1) b0 x[kм k(t)k y ]

и выбирается функция Ляпунова

				3
	V (		, ) xi pij x j			2
	V (	x	, ) xi pij x j			2
				i, j 1			,
				где
	k м k y k (t)						.
							.
Определяется производная функция Ляпунова
	2			2	2	2 2( p31x1
	2			2	2
V (x, ) q11x1				q22 x2	q33 x3

	p32x2 p33x3) k м k y k(t) x,

где

q11=2b0p31 > 0; q22=2(b1p32-p12) > 0; q33=2(b2p33-p12)>0.

Алгоритм настройки коэффициента усиления системы находится в виде

k y 1 p31 p32 (1) p33 (2) x.

Вторым методом Ляпунова выявляются достаточные условия устойчивости, поэтому для построения управляющего устройства часто требуется слишком большой объем информации, и система оказывается сложной по структуре. Однако синтезированную таким образом СНС удается затем упростить, используя на втором этапе построения другие, менее общие методы, с проверкой результатов моделированием.

1.8. Беспоисковые самонастраивающиеся системы с моделью и контролем частотных характеристик

Стабилизация динамических характеристик объекта управления при минимально-фазовом основном контуре

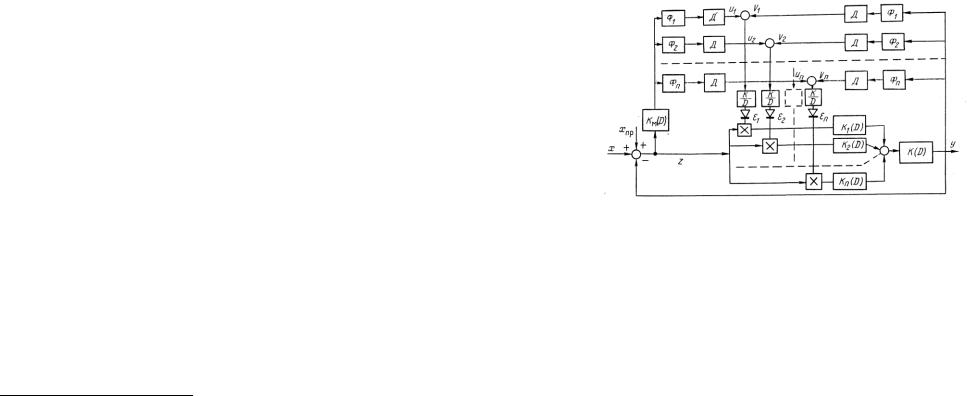
управления может осуществляться путем контроля одной частотной характеристики, например амплитудной. Соответствующая схема приведена на рис. 1.20. Основными элементами системы являются объект управления с исполнительным устройством K(D)1 линейная модель, или эталон, Kм(D), к частотным характеристикам которой должны стремиться частотные характеристики основного контура путем самонастройки, и настраиваемое последовательное корректирующее устройство. Это устройство состоит из параллельных ветвей (n ≥ 1). Каждая ветвь содержит звено с переменным коэффициентом усиления εi и фильтр Ki(D). Выходные сигналы всех ветвей суммируются и подаются на исполнительное устройство.

1 Удобный способ записи дифференциальных уравнений, особенно для описания нелинейных систем, основывается на использовании символа

дифференцирования по			времени D	d	. При этом, например,		дробь
				dt

Kyx(D)	K	называют	алгебраизированной			формой	записи

	1 DT

передаточной функции, которая формально для линейной системы сводится к замене p D . Часто это выражение называют передаточной

функцией. Напомним, что строгое определение передаточной функции дано в гл. 1. Соответствующее этой передаточной функции алгебраизированное уравнение имеет вид

y(t)=Kyx(D)x(t).

Частотная характеристика в этом случае из передаточной функции определяется подстановкой D=jω.

Рис. 1.20. Схема беспоисковой СНС с контролем характеристик основного контура.

Число ветвей выбирается в соответствии с числом переменных параметров объекта, требуемой точностью стабилизации и допустимой сложностью системы. При изменении двух параметров объекта можно, например, принять n = 1, несколько снизив точность стабилизации.

Передаточная функция корректирующего устройства равна

n
i Ki (D)
i 1	.

При выборе передаточных функций фильтров Ki(D) необходимо исходить из того, чтобы при любой (в пределах заданной области) характеристике объекта существовали значения параметров настройки εi, при которых имело бы место приблизительное равенство

K (D) i Ki (D) K м (D)

i 1

и физическая реализация была достаточно простои.

K м ( j i )

Очевидно, для любой (в пределах заданной области) амплитудно-частотной характеристики объекта должны существовать значения параметров, при которых

n	K м ( j )
i Ki ( j )	K м ( j )		.	(1.70)

		K ( j )

i 1
i 1

В качестве фильтров корректирующего устройства удобно применять резонансные фильтры с достаточно большим затуханием.

Для определения значений параметров настройки интервал рабочих частот, равный (1,5—3)ωс модели, разбивается на п рав- 3 ных интервалов с рабочими частотами

ωυ = υΩ (υ = 1,2,….n).

Из условия (1.70) следует, что:

K ( j ) i Ki ( j ) K м ( j )

i 1

Для достаточно узкополосных (1.71) принимает вид

K ( j i ) i Ki ( j i ) K м ( j i )

или

i K ( j i ) Ki ( j i )

(υ = 1,2,….n). (1.71)

фильтров уравнение

(i = 1,2,…,n).

Для устранения влияния неоднозначности в схеме рис. 1.20 перед вторыми входами множительных звеньев включаются линейные детекторы (вентили). Такие вентили пропускают лишь неотрицательные значения параметров

настройки εi. В приведенной схеме осуществляется непрерывный: контроль амплитудной частотной характеристики в ряде точек ω = ωυ на участке от входа сигнала рассогласования до выхода системы. Контроль осуществляется с помощью пробного сигнала xпр, подаваемого от специального генератора на вход модели и системы. Целесообразен регулярный пробный сигнал в виде периодической функции времени с равномерным в диапазоне

рабочих частот линейчатым спектром xпр a cos t .

Выходная величина модели подается на узкополосные резонансные фильтры Фυ, настроенные на рабочие частоты ωυ = υΩ. Через такие же фильтры пропускается выходная величина системы у.

Сигналы с выходов фильтров выпрямляются детекторами Д. Выходные сигналы детекторов (их амплитудные значения) попарно вычитаются и подаются на интегрирующие звенья, которые через вентили соединяются со вторыми входами множительных звеньев корректирующего устройства. При εр>0 (p = 1, 2, ... , n)

D p p K p U p Vp ,

где Кр — коэффициенты усиления интегрирующих звеньев;

|Up| и |vp| — амплитудные значения сигналов у элементов сравнения со стороны выхода модели и выхода системы.

Если полосы пропускания фильтров корректирующего

устройства меньше или равны , то в системе при εр>0

автоматически устанавливаются значения параметров настройки εр = εр0 , соответствующие совпадению амплитудных частотных характеристик в п точках:

K jp

(p = 1,2,…, n)

(1.72)

1.9. Самонастраивающиеся по входному сигналу системы

1.9.1. Самонастраивающиеся по входному сигналу системы с разомкнутыми цепями настройки

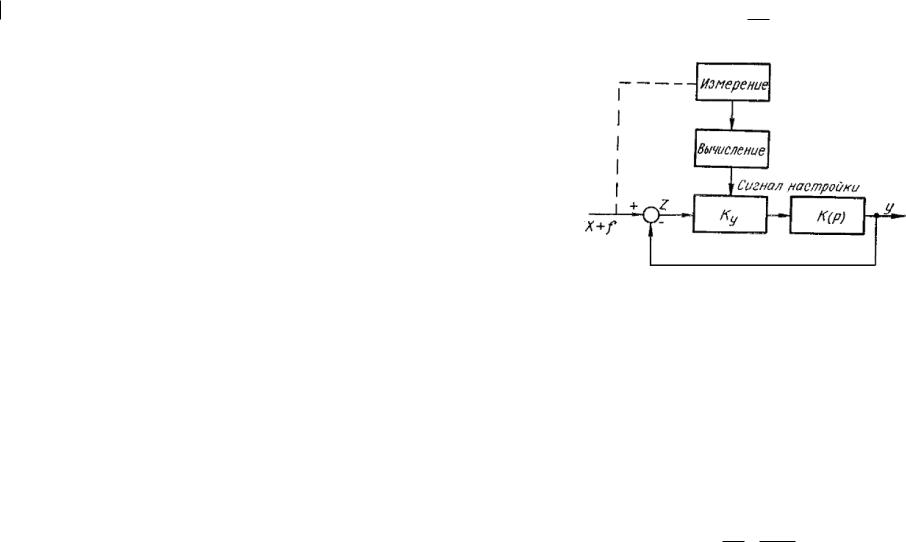
Всамонастраивающихся по входному сигналу системах осуществляется их оптимизация при изменении характеристик, задающих воздействий и помех. Для такой оптимизации необходимо измерение параметров спектральных плотностей воздействий и помех или измерение показателя качества, косвенно определяющего эти значения.

ВСНС с разомкнутыми цепями настройки используются специальные устройства для определения текущих характеристик входного сигнала. Работу такой системы рассмотрим при воздействии на ее входе задающего сигнала в

виде регулярной функции времени x(t) = Vt и случайной помехи f(t) со спектральной плотностью Sj( ) = a2 (рис. 1.21). Передаточная функция системы

K( p)	K		,	K K y K.
	p(1	Tp)

Система самонастройки, воздействующая на коэффициент преобразования Kу, должна обеспечивать минимум суммарной среднеквадратичной ошибки системы, независимо от скорости изменения входного сигнала в установившемся режиме. Задающее воздействие и помеха не коррелированны.

С помощью коэффициентов ошибок находим

z 2 V 2 .

д K 2

Рис. 11.21. Схема самонастраивающейся по входному сигналу системы с разомкнутой цепью настройки.

Дисперсия от помехи

a2 K

( j)2

( j) 1

следовательно, средний квадрат суммарной ошибки равен

Z 2 V 2 a2 K ,

K 2

Условие минимума среднеквадратичной ошибки выполняется при

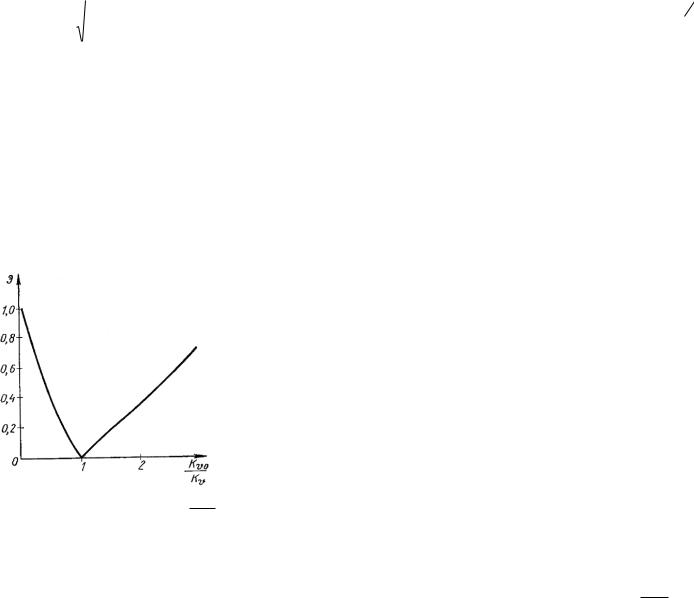
		4V 2	1	2	2

K	3		43 V 3 a		3 .
K	3	a2	43 V 3 a		3 .
опт		a2

Таким образом, для оптимального управления с минимумом среднеквадратичной ошибки Z2 при переменной скорости V входного сигнала и изменяющейся спектральной плотности помехи Sj( ) необходимы измерительные устройства для измерения V и а2, а также два функциональных преобразователя.

Если Sj( ) = const и известно, что скорость задающего сигнала изменяется в некотором диапазоне

Vmin V Vmax ,

Рис. 1.22. Зависимость Э = f ( K 0 ).

то диапазон изменения коэффициента преобразования определится соотношением

опт max

max

(1.73)

опт min

Vmin

Эффективность самонастройки можно оценить по

формуле

Э 1

Z 2

где

и Z

- соответственно

суммарная ошибка

оптимальной самонастраивающейся системы и системы без самонастройки.

Так как

3V 2

2V 2 a2 K 3

K 2

2K 2

опт

то

Э 1

3 K 0

Зависимость

, приведенная на рис. 1.22,

показывает, что эффективность самонастройки может быть существенной при двукратном и более различии коэффициентов преобразования самонастраивающейся и соответствующей системы без самонастройки.

Учитывая выражение (1.73), можно сделать вывод о целесообразности самонастройки при условии, что

Vmax 2.

Vmin

<<< < Предыдущая 1 2 34 / 174 5 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20223.92 Mб8Учебное пособие 2010.pdf
#
30.04.20223.92 Mб3Учебное пособие 2011.pdf
#
30.04.20223.93 Mб2Учебное пособие 2012.pdf
#
30.04.20223.96 Mб4Учебное пособие 2013.pdf
#
30.04.20223.97 Mб3Учебное пособие 2014.pdf
#
30.04.20223.99 Mб8Учебное пособие 2015.pdf
#
30.04.20223.99 Mб1Учебное пособие 2016.pdf
#
30.04.20224.01 Mб6Учебное пособие 2017.pdf
#
30.04.20224.03 Mб4Учебное пособие 2018.pdf
#
30.04.20224.06 Mб6Учебное пособие 2019.pdf
#
30.04.2022326.63 Кб10Учебное пособие 202.pdf

q11		0	0		0	0	b0			p11	p12	p13
q11		0	0		0	0	b0			p11	p12	p13
0		q22	0		1	0		b1		p21	p22	p23
0		0	q33		0	1	b2			p31	p32	p33
	p11	p12	p13	0		1			0
	p11	p12	p13	0		1			0
	p21	p22	p23	0		0				.
	p31	p32	p33	b0		b1		b2

q11		0	0		0	0	b0			p11	p12	p13
q11		0	0		0	0	b0			p11	p12	p13
0		q22	0		1	0		b1		p21	p22	p23
0		0	q33		0	1	b2			p31	p32	p33
	p11	p12	p13	0		1			0
	p11	p12	p13	0		1			0
	p21	p22	p23	0		0				.
	p31	p32	p33	b0		b1		b2

q11		0	0		0	0	b0			p11	p12	p13
q11		0	0		0	0	b0			p11	p12	p13
0		q22	0		1	0		b1		p21	p22	p23
0		0	q33		0	1	b2			p31	p32	p33
	p11	p12	p13	0		1			0
	p11	p12	p13	0		1			0
	p21	p22	p23	0		0				.
	p31	p32	p33	b0		b1		b2