Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 2015

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

3.99 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 176 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Экстремальное значение Kу определяется из условия

dKd y mz2 z2 Ky Ky.опт 0,

где mz2 и z2 заданы выражениями (1.86) и (1.87).

При заданных функциях Кc и Тс находим оптимальное значение коэффициента усиления корректирующей цепи

Ку.опт(t).

Рис.2.1 Блок-схема синтезируемой системы.

ГЛАВА 2 ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ С АКТИВНЫМ

ПОИСКОВЫМ ВОЗМУЩЕНИЕМ

2. 1. Метод синтеза непрерывных экстремальных систем управления

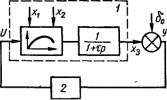
В основе метода лежит замена нелинейного экстремального объекта с постоянными параметрами при наличии помех на его входе и выходе линейным звеном со случайно флуктуирующими параметрами, и затем применение к такому объекту метода синтеза оптимального фильтра, предложенного в работе Калмена и Бэси [84]. Объект аппроксимируется последовательным соединением (рис.

2.1) нелинейного параболического звена и линейного инерционного

звена первого порядка. При этом возмущения 1 и 2

представляют собою броуновские движения (процессы на выходах интеграторов, которые возбуждаются белым шумом), помеха 0 — белый шум. Возмущениях, и 1 -сдвига от точку

экстремума по горизонтали и вертикали соответственно. Система дифференциальных уравнений, описывающая

динамику такого объекта, записывается в виде

dx1				(2.1)
dt		1,		(2.1)
		1,

dx2				(2.1а)
dt			2,	(2.1а)
			2,

	113

dx3

k u x1

(2.1б)

(k—крутизна параболы).

При этом наблюдаемый сигнал

y x3 0

(2.1в)

Цель управления — минимизировать величину потерь

k(u x )2 .

(2.2)

Минимизация (2.58) может быть достигнута, если известна координата x1 (t) . Обозначим наилучшую оценку величины x1 (t) через m1 (t) , а наилучшие приближения к

m (t)	— через m(1)	(t) . Введем понятия «умышленной»
1	1
(intentional) ошибки
		g (1) (t) u(t) m(1)			(t)	(2.3)
				1
и «неумышленной» (unintentional) ошибки
		e(1)	(t) x (t) m(1)		(t)	(2.4)
		1	1	1

Первая ошибка названа «умышленной», так как для оценки параметров объекта приходится на управляющий сигнал и(t) накладывать пробный (поисковый) сигнал; вторая ошибка является результатом неточной оценки положения экстремума.

Из уравнений (2.3) и (2.4) следует

u x	g (1)	e(1)	d e	,	(2.5)
1		1	1

так как сигналы g и e1 получаются простой заменой

114

m(1)	(t) на m (t)					в (2.3) и (2.4);
1	1
	С учетом (2.5) перепишем (2.2) в виде

							1	k(g e )2			1		k(g (1)	e(1) )2
		f					1				1
		f
						2			1	2				1
						2				2					(2.6)
				1	k g (1)2										(2.6)

									e(1)2			kg (1) e(1)
									e(1)2			kg (1) e(1)
			2						1
			2

Строго говоря, член kg (1) e(1) в равенстве (2.6), который

представляет собою корреляцию между «умышленной» и «неумышленной» ошибками, не равен нулю. Если учесть, что

сигнал g (1) (t) образован поисковым сигналом (в дальнейшем под g (1) (t) понимается поисковый сигнал), а сигнал e(1) (t)

есть следствие действия на систему внешних помех, которые некоррелированы с поисковым сигналом, то такое рассуждение имеет лишь качественный характер и, вообще говоря, не строго. Обозначим через x(t) сигнал х(t),

прошедший через звено первого порядка с постоянной времени η. Тогда сигнал x3 с учетом (2.4) равен

x		1	k(u x )2	x		1	k(g (1)2	2e(1) g (1)	e(1)2 ) x
	3				2					2
		2	1			2		1	1

а наблюдаемый сигнал у равен:

y x3 0 kg(1) x1 x2 12 k g (1)2 2m(1) g (1) e1(1) 2 0 .

(2.7).

Как будет показано ниже, в синтезируемом экстремальном регуляторе используется для управления не наблюдаемый сигнал у,

а сигнал y (1) ,определяемый уравнением

	y(1) y	1	k g (1)2		2m(1) g (1)				C		,			(2.7а)
	y(1) y		k g (1)2		2m(1) g (1)				C		,			(2.7а)
	2									11
	2

где C	-дисперсия сигнала e(1) 2 , т. е.							C	e(1)2 . Обозначим
11	1							11	1
через
		g (1) (t) e(1)2 C							.					(2.7б)
					1			11
Тогда уравнение сигнала (2.7а) с учетом (2.7) и (2.9)
перепишется в виде
	y(1) kg (1) x x					1	k g (1)		(t)				.	(2.7в)
	y(1) kg (1) x x			2			k g (1)		(t)			0	.	(2.7в)
	1			2	2							0
					2

Линеаризация системы сводится к отбрасыванию члена

ε k2 g (1) (t) в уравнении (2.7в), что справедливо при малых

k, а также в том случае, когда частотный спектр этого сигнала существенно меньше по мощности, чем частотный спектр сигнала x2 , поскольку влияние нелинейности сводится к

добавлению kx2 величины ε.

Тогда приближенное значение выходного сигнала может

быть выражено	(0) kg(1) x x
y	(0) kg(1) x x		0	.	(2.8)
	1	2	0
Задача сводится к выделению из сигнала y (0)					величины
x1 (2.8). На рис. 2.2 приведена блок-схема, где l - линейный
элемент со случайно изменяющимся наклоном x1					и
аддитивным шумoм x2	на выходе; 2 — линейное инерционное
звено;
	116

115

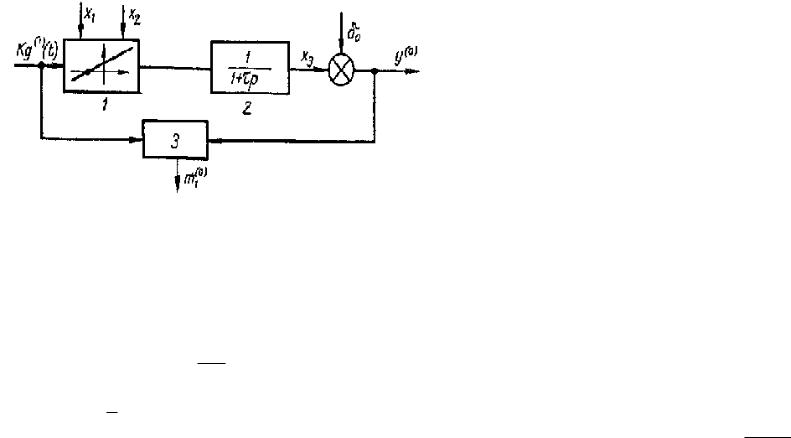
3 — оптимальный фильтр для оценки m1(0) ; математического

Рис. 2.2.Эквивалентная блок-схема синтезируемой системы.

ожидания сигнала x1 . При этом kg (1) (t) в данной схеме

является пробным (поисковым) сигналом, который вводится в

систему для оценки случайно изменяющегося коэффициента усиления x1 . Показатель качества управления приближенно выражается (2.6):

	1	k g (1)2	e(1)2	.	(2.9)
f

2			1

Поэтому f можно уменьшить, если сделать поисковый сигнал g (1) (t) предопределенной функцией времени. Система,

представленная на рис. 2.2, описывается системой дифференциальных уравнений (в канонической форме) следующего вида (см. (2.1) —( 2.1в)):

117

	x			0	0	0					x
d			1									1
d				0
		x	2		0	0					x	2		,	(2.10)
		x			0	0					x			,	(2.10)
dt				kg	1		1
dt				kg	1		1				(0)
													0
	x3							x3					0

				y(0) x(0)					0	.					(2.11)
					3				0

Система может быть записана в векторной форме:

dx0	a(t)x0	,			(2.12)
dt	a(t)x0	,			(2.12)
dt
y(0)	S' x(0)		0	.	(2.57)
			0

Здесь а (t) — матрица в правой части (2.10); S' —вектор-строка [0, 0, 1].

Пусть Ь — матрица спектральных плотностей белых шумов b1 и b2 .

b11		b12	0

b b21		b22	0	,
	0	0	0

математические ожидания переменных x2 и x3 —

соответственно m2(0) и m3(0) , а спектральная плотность помехи

0 b00 .

В[84] показано, что ковариационная матрица

C/cov ху = х(t)y(t) cov x x(t) 2 / и математическое ожидание

m(0) случайного вектора x x2 определяется из

118

системы уравнений:

dm(0)

am(0)

CSy(0) S' m(0) ,

(2.14)

b00

dC(0)

ac ca' b

CSS'C .

(2.15)

b00

При этом элемент C11 матрицы С означает, очевидно,

дисперсию сигнала ошибки e(1) 2 . Обозначим поисковый

сигнал kg (1) (t) через r ( t) . Здесь. r — амплитуда

поискового сигнала; ω — частота; ψ отражает форму

поискового сигнала.

Введем безразмерныe нормированные параметры, такие,

что в новом масштабе спектральные плотности b00 , b11 ,

b33

становятся

B11 B22 B00 1.

Тогда

b11

b22

b00

T t(b b )

b22

b12

sin , - белый шум с единичной

b11b22

спектральной плотностью;

119

- белый шум с матрицей (спектральных плотностей).

sin

(2.15a)

sin

X 1M1 E1

x1 , m1 , e1 ,

b11 b00b22

, m

, e

b00b22

X 3 M 3 E3Y

x3 , m3 , e3 , y

C11

C11 ; C12

,C13

C12 ,C13 ,

(2.16)

b11

b00b22

b00b11

C22 ,C23 ,C33

C22 ,C23 ,C33 ,

b00b22

KG (1) (T ) R ( T )

b11

kg (1) (t),

b22

C33 C33

Обозначим

k 2b

;

b00

;

b00

(2.17)

b11

b12

С учетом (2.16) развернем систему уравнений (2.14) и (2.15):

120

											dm(0)		C ( y(0)							m(0) ),
												1																						(2.17а)
									1																									(2.17а)
									1		dt					13						3
											dt
										dm(0)			C					( y(0)		m(0) ),
												2																						(2.17б)
								2								23																		(2.17б)
								2			dt					23						3
											dt
dm(0)			r ( t)m(0) m(0)															m(0)			C				( y(0) m(0) ),
3																																		(2.17в)
																								33										(2.17в)
dt										1				2					3					33								3
dt
m(0)				[r ( t)m(0)									m(0) C								33	( y(0)			m(0) )]						3		,	(2.17г)
3												1		2							33						3				3
						dC11					1 C 2			,	dC12				sin C C										,
											1 C 2			,					sin C C									22	,
							dT						13			dT									13			22
							dT									dT
													dC22				1 C				2	,
																	1 C					,
													dT							23
													dT
			dC13					1 R (T )C											1C					C C						,				(2.18)
								1 R (T )C											1C					C C						,				(2.18)
				dT														11					12			13			33
				dT
				dC23							1											1
												R (T )C											C		C			23	C	33		,
												R (T )C											C		C				C			,
				dT														11						12
				dT
	dC33				2 2 1 R (T )C 1C																								C				2 .
					2 2 1 R (T )C 1C																						23		C				2 .
		dT																				13					23					33
		dT

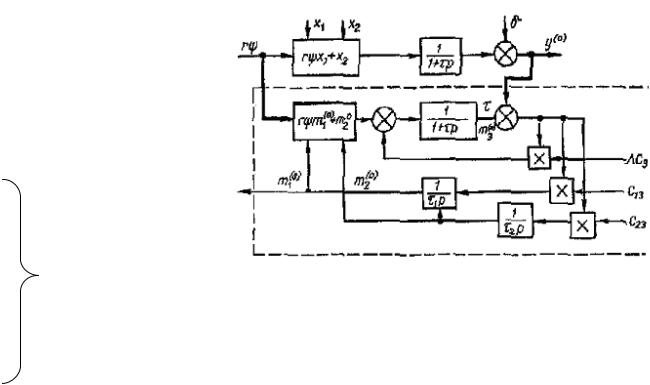
Если положить в уравнение (2.17), что C13 , C23 , C33

представляют собою некоторые известные функции времени (сигналы), то система (2.17 а, б, в) описывает схему оптимального демодулятора, который наилучшим образом оценивает величину m1(0) — математическое ожидание сигнала x1 , т. е. элемент 3 в блок-схеме рис. 2.2. Схема этого фильтра

приведена на рис. 2.3.

Рис. 2.3. Синтезированная блок-схема

оптимального фильтра.

Сигналы C13 , C23 , C33 находятся из системы уравнений (2.18) для заданных поисковых сигналов k ( ,t) либо с

помощью аналитического решения этих уравнений, либо с помощью моделирования или численного решения. Уравнения (2.18) моделировались и решались для сигналов k ( ,t) при

различных формах сигналов ψ, амплитудах r и частотах ω с целью нахождения оптимальных формы, частоты и амплитуды пробных сигналов, минимизирующих C11 (дисперсию сигнала

ошибки). Формы сигналов C13 , C23 , C33 для разных k ( ,t) представлены на рис. 2.4. При этом оказалось, что оптималь

122

121

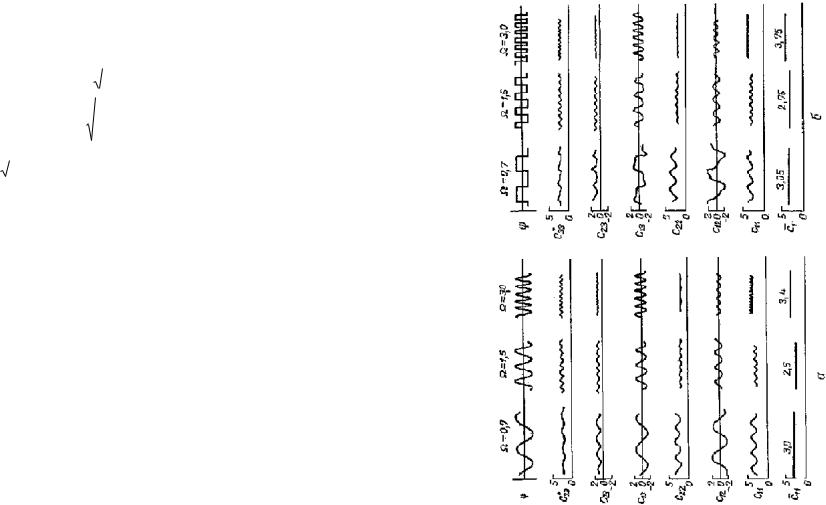
ной формой поисковых движений является синусоида, а остальные оптимальные параметры настройки будут

			opt		1				,


						1		2				(2.19)
						1		2

			ropt	3		J	0	.
						J	0
						1


	1						m(0)			, m(0)	и m(0)
Здесь J	1	cos	1 2 . Оценки									, получены
Здесь J		cos	1 2 . Оценки									, получены
2								1		2	3
2

нами на основе линейной модели объекта, выходной сигнал,

которой равен y (0) . В исходной же задаче нами используется

сигнал y (1) , определяемый из (2.7а). Оценки																m , m		2		, m		3	,
																	1	2				3
полученные в результате наблюдения за y (1) (t) обозначим
соответственно через								m (1) ,		m (1) и	m(1)		и подставим их в си-
								1		2	3
стему уравнений (2.17а, б, в). Найдем способ получения																								m (1)	,
																								1
m2(1) и m3(1)				из исходного сигнала у, воспользовавшись
уравнениями (2.8а) и (2.176) и учтя обозначение kg r :
	(1)		(1)			k		(1)2				(1)				(1)			(1)
y		m	3	y			(g		C ) m			2	C	33	( y		m		3		)			(2.20)
y		m		y			(g		C ) m				C		( y		m				)			(2.20)
										11
					2

или

y(1) m(1)	y ,	(2.20б)
3

где μ равно второму слагаемому правой части (2.20)

Рис. 11.4. Формы сигналов.

124

123

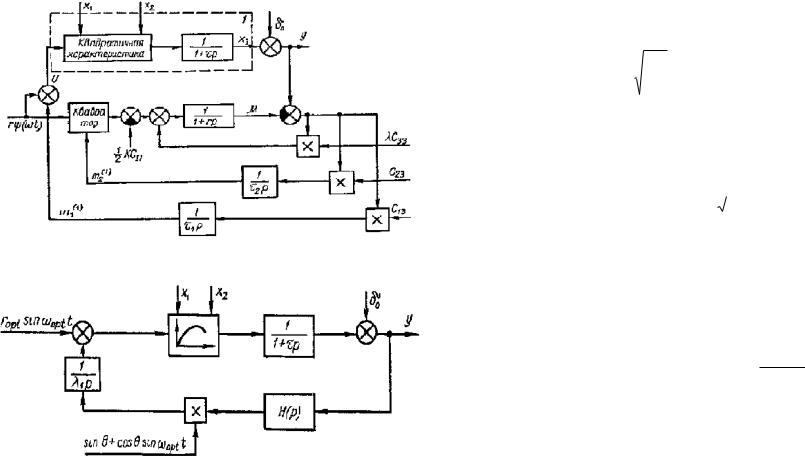
Рис. 2.5. Пример синтезированной экстремальной системы.

Рис. 2 6. Упрощенная блок-схема экстремальной системы для случая, когда x1 x2 .

Таким образом, вместо сигнала y(1) m3(1) в уравнениях

(2.17а) — (2.17г) используется сигнал у + μ. Структурная схема синтезированного таким образом экстремального

125

регулятора представлена на рис. 2.5.

Существенное упрощение блок-схемы получается при

малых R		b11	r , т. е. когда шум x						много мощнее шума x .
малых R			r , т. е. когда шум x					2	много мощнее шума x .
		b22						2					1
		b22
Рассмотрение уравнений (2.17а, б, в) и (2.18) при
r ropt , opt			показывает, что блок-схема системы
приводится к виду (рис. 2.6), где
	H ( p)				2 p(1			p)				.	(2.21)

				1							p 2
				1	1 2	2	p			2	p 2
						2			1	2

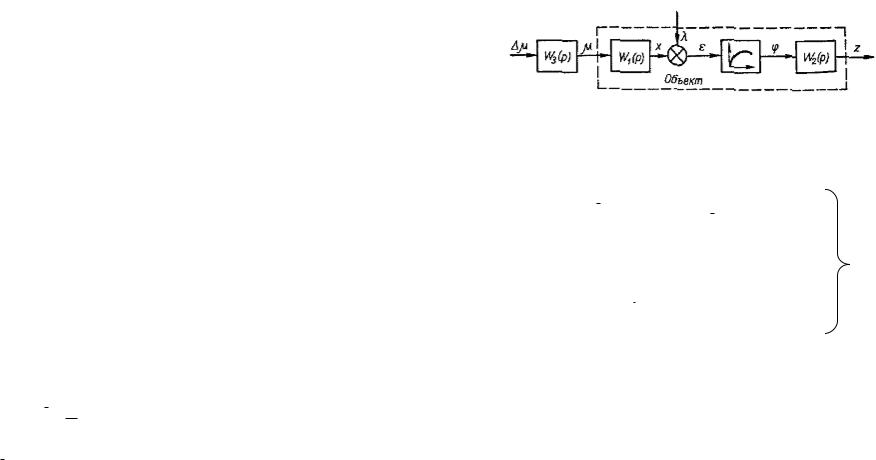
Как следует из рис. 2.6, при отсутствии корреляции между 1 и 2 (или x1 и x2 ), т. е. при sin ζ=0, оптимальный регулятор является простым оптимизатором с синхронным детектором и корректирующим звеном Н (р) Если же и 0 ( 0) , т. е. отсутствует инерционность на выходе объекта, то

H ( p)	2 p
H ( p)	2 p 1 .	(2.21а)

В этом случае корректирующее устройство представляет собою реальный дифференциатор.

126

2. 2. Переходные и установившиеся процессы в импульсных системах экстремального регулирования.

Динамика импульсных систем экстремального регулирования (ИСЭР) описывается нелинейными разностными уравнениями. Как известно, разностные уравнения представляют собою достаточно простые рекуррентные соотношения. Поэтому построение переходных процессов в импульсных экстремальных системах может быть осуществлено численным решением соответствующих рекуррентных соотношений. Анализ устойчивости установившегося состояния, а также поведения СЭР при равномерном дрейфе экстремума требуют разработки специальных методов применительно к конкретным типам ИСЭР. Рассмотрим методы исследования переходных процессов в импульсных экстремальных системах.

2.2.1. Метод составления разностных уравнений динамики ИСЭР.

Этот метод сводится к составлению несложных алгоритмов, легко реализуемых на простейших ЦВМ. Составление разностных уравнений динамики основано на интегрировании дифференциальных уравнений движения звеньев внутри одного периода регулирования (используя

безразмерное время t Tt , где Т — интервал дискретности) и

последующей дискретизации полученных решений

(приравнивая t 1) [40, 63]. Допустим, что объект представляет собою параболическое звено с инерционными

127

элементами W1 ( p) на входе и W2 ( p) на выходе (рис 2.32). Если W1 ( p) и W2 ( p) — инерционные звенья первого порядка,

то динамика объекта внутри s-гo периода дискретности описывается уравнениями:

Рис. 2.7. Аппроксимация объекта оптимизации.

dxS (t)

xS (t) k1

S (t),

d t

(t) k

(t)

(t)]2

(2.22)

f (s),

zS (t) kH

[xS ( ) S ( )]2 (

Здесь

1 , k1 — постоянная времени и коэффициент усиления

первого звена,

k H

— коэффициент при параболе,

f (s) — дрейф экстремума по произвольному закону (в

случае переходного процесса S

CONST );

128

(t) k2 e 2 — функция веса второго звена.

Решая эти уравнения для начальных условий

xS (0) xS 1 , zS (0) zS 1 и т. д. и приравнивая

= 1, получим

систему разностных уравнений, описывающих динамику

объекта в переходном процессе (поиск из начального

состояния S CONST ).

xS dxS 1 (1 d ) S ,

( x

[(

S 1

)2 2(1 d )(

S 1

)

(2.23)

(1 d ) 2 d (1 d )(x

S 1

2 d (xS 1 S )( S )].

Кэтим уравнениям следует присоединить уравнение сервомотора (на рис. 2.6—Wз (s))

S 1 S ,

(2.24)

и соответствующего регулятора, например разностного регулятора с синхронным детектором

S (k S 1 aM )( 1)3 ,

(2.25)

где k -- коэффициент усиления регулятора,

aM — амплитуда модуляции;

или присоединить уравнение релейно-импульсного регулятора

129

S q sign zS 1 sign S 1 ,

(2.25a)

где q — величина шага, или любого другого регулятора,

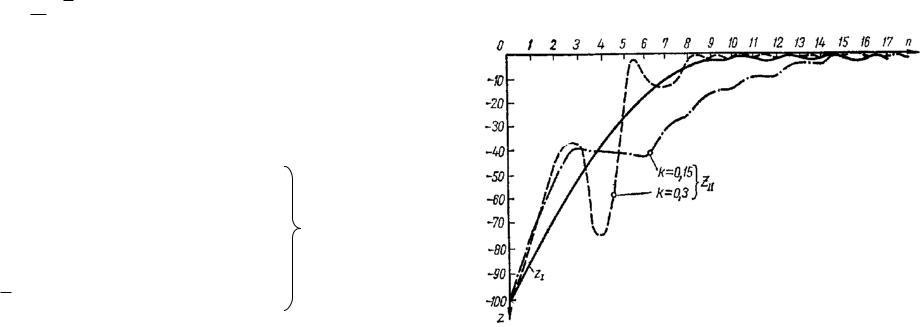
Рис. 2.7. Переходные процессы в релейно-импульной Z1 и пропорционально-импульсной системах Z11 .

например релейно-импульсного регулятора с импульсной коррекцией (об импульсной коррекции см. ниже) и т. д. Система рекуррентных уравнений (2.23) — (2.25) решается аналитически или на ЦВМ.

Типовые переходные процессы для регулятора с синхронным детектором при разных k (кривые Z11 ) и для релейно-импульсного регулятора с импульсной коррекцией

130

<<< < Предыдущая 1 2 3 4 56 / 176 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20223.92 Mб8Учебное пособие 2010.pdf
#
30.04.20223.92 Mб3Учебное пособие 2011.pdf
#
30.04.20223.93 Mб2Учебное пособие 2012.pdf
#
30.04.20223.96 Mб4Учебное пособие 2013.pdf
#
30.04.20223.97 Mб3Учебное пособие 2014.pdf
#
30.04.20223.99 Mб8Учебное пособие 2015.pdf
#
30.04.20223.99 Mб1Учебное пособие 2016.pdf
#
30.04.20224.01 Mб6Учебное пособие 2017.pdf
#
30.04.20224.03 Mб4Учебное пособие 2018.pdf
#
30.04.20224.06 Mб6Учебное пособие 2019.pdf
#
30.04.2022326.63 Кб10Учебное пособие 202.pdf