Учебное пособие 2015

51.Попов Е.П. Динамика систем автоматического регулирования ГИТТЛ, М., 1954.

52.Савин О. Р.— Автоматика, 1964, 2.

53.Соколов Ю. Д.— Укр. математ. журнал, 1957, 9, 4. 54.Стратанович Р. Д.— Советское радио, 1961. 55.Степанов А. Д. Автоматическое регулирование

мощности в тепловозах и газотурбовозах. Машгиз, М., 1960. 56.Тарасенко В. П.— Изв. АН СССР. ОТН. Техническая

кибернетика, 1963, 2.

57.Тарасенко В. П.— Изв. АН СССР. ОТН. Техническая кибернетика,1963,3.

58.Товстуха Т. И.—В кн.: Автоматическое регулирование и управление. Изд-во АН СССР, М., 1962.

59.Товстуха Т. И — Автоматика и телемеханика, 1960,

21, 5.

60. Ту Ю.Т. Цифровые и импульсные системы автоматического управления. «Машиностроение», М., 1564.

61.Туник А. А. — Автоматика, 1962, 6. 62.Туник А. А. — Автоматика, 1963, 5. 63.Туник А. А.. — Автоматика. 1964, 1.

64.Туник А. А.— Изв. АН СССР. ОНТ. Техническая кибернетика, 1965, 1.

65.Туник А. А.— Автоматика, 1965, 2.

66.Фельдбаум А.А.—Автоматика и телемеханика,1959, 8. 67.Фельдбаум А. А. Вычислительные устройства в

автоматических системах. ГИФМЛ, М , 1959. 68.Фицнер Л. Н.— Электричество, I960, 8.

69.Фицнер Л. Н.—Автоматика и телемеханика,1960,21, 8. 70.Цыпкин Я. 3.— Автоматика и телемеханика, 1963, 12. 71.Цыпкин Я.З. Теория релейных систем

автоматического регулирования. Гостехиздат., М., 1955.

231

72.Цыпкин Я.З. Теория линейных импульсных систем. Физматиздат., М., 1S63.

73.Эвелий В. У. Дискретные и самонастраивающиеся системы.— В кн.: Труды 2 Международного конгресса ИФАК. «Наука», М., 1965.

74.Юркевич А. П.— В кн. Автоматическое управление и вычислительная техника. 4. Машгиз., М., 1961.

75.Чанг Ш. Сл. Синтез оптимальных систем автоматического управления. «Машиностроение», М , 1964

76.Черныш А. Ф. Системы автоматического судовождения на реках. Изд. во АН УССР, К., 1963.

77.Чинаев П. И.— Автоматика, 1961, 3.

78.Чинаев П. И. Самонастраивающиеся системы. Расчет и проектирование. Машгиз., М., 1963.

79.Bernard J. W., Soderquist F. J.—Control Eng., 1959, Nov. 80.Fгеу A. D., Dum W. B. An application of Sampled — Data Adaptive Optimization Joint amencan Control Conference,

1965.

81.Roberts J. D. — Proc. Inst. Electron. Gngrs. 1965, 112. 82.Vanhice R.T., Mathias R.A. Adaptive Control Systems

Pergamon Press. Oxford — London — New York — Paris, 1963. 83.Sawaragi I, Sugai, Sunahgra J. Statistical Studies of Non-

Linear Control Systems Osaka, Japan, 1962.

84.Ка1man R. Bucy Trans. ASME, J. Basic Eng., ser. D-81,

1961.

232

ГЛАВА 3. БЕСПОИСКОВЫЕ ЭКСТРЕМАЛЬНЫЕ РЕГУЛЯТОРЫ

3.1. Дифференциальные системы экстремального управления без поисковых колебаний.

Все поисковые экстремальные системы не лишены основного своего недостатка, вытекающего из принципа их построения, а именно — поисковых колебаний. Этот недостаток объясняется тем, что ориентация поисковых систем относительно экстремума основана либо на естественных, либо на искусственных поисковых колебаниях. Другим недостатком подавляющего большинства всех поисковых экстремальных систем является их сравнительно низкая помехоустойчивость. Управляющий сигнал, вырабатываемый этими системами, пропорционален не только ошибке, т. е. удалению системы от экстремума, но и помехе, т. е. возмущениям, перемещающим экстремальную характеристику объекта регулирования в вертикальном направлении.

Многие производственные объекты, обладающие экстремальной характеристикой, не допускают поисковых колебаний. Это вызывает необходимость создания систем, решающих экстремальную задачу без применения поисковых колебаний.

Обычно нелинейная часть экстремальных объектов сравнительно просто поддается моделированию. Примером этого могут быть многие объекты химической промышленности, один из которых будет подробно рассмотрен в дальнейшем. В указанных объектах из основного резервуара легко отбирать небольшие пробы в специальные пробники (датчики), и на основании этих проб строить модели.

Пусть объектом оптимального регулирования является какой-либо резервуар, наполненный веществом определенного качества. Задача состоит в поддержании экстремального значения этого показателя качества. Допустим сначала, что управление объектом ведет оператор. Для определения качества вещества оператору необходимо взять пробу из основного резервуара в специальный пробник (например, в пробирку). Вещество, отобранное в пробник, уже испытало действие всех регулирующих и возмущающих воздействий. Пробник в данном случае является как бы миниатюрной моделью объекта. Если оператор будет действовать по принципу поисковых экстремальных систем, то ему необходимо взять две пробы: одну до введения управляющего воздействия, другую — после. На основании анализа этих проб оператор определяет направление дальнейшего изменения управляющего воздействия, соответствующее приближению показателя качества к экстремуму.

Эту задачу можно решить и другим способом, взяв две пробы одновременно. При этом в один из пробников добавляется вещество, соответствующее определенному увеличению управляющего воздействия. В другой пробник Добавляется вещество, соответствующее такому же по величине уменьшению управляющего воздействия. На основании анализа этих проб можно определить нужное направление изменения управляющего воздействия. На принципе анализа проб, взятых одновременно, основано действие описываемой системы экстремального управления.

Функциональная схема такой системы приведена на рис. 2I.1. Управляющие (x) и возмущающие ( , ) воздействия в этой системе действуют не только на объект управления, но и

234

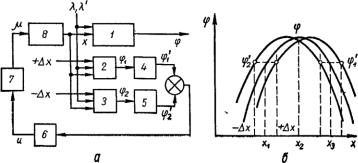
на две модели. Кроме того на эти модели действуют одинаковые и постоянные по модулю, но различные по знаку дополнительные управляющие воздействия x , в результате чего статические экстремальные характеристики моделей смещаются относительно характеристики объекта в одной модели вправо, в другой—влево (рис. 2I.1, б).

Рис. 3.1. Дифференциальная система экстремального управления, использующая принцип сдвига характеристик:

а— структурная схема; б — статические характеристики:

1— нелинейная безынерционная часть объекта; 2,3— модели объекта; 4,5,6 — усилители;7 — исполнительный элемент;

8 — линейная инерционная часть объекта. Рассмотрим этот процесс более подробно. Предположим,

что на вход обеих моделей и на объект регулирования подается регулирующее воздействие x1 . Тогда выходная величина первой модели, соответствующая (x1 x) , будет равна 1' , а выходная величина второй модели соответствует (x1 x) и равна 1' . Те же самые рассуждения можно провести и для случая, когда на вход моделей и объекта регу-

235

лирования подается регулирующее воздействие x3 .

Рассмотрев ряд значений регулирующего воздействия, можно убедиться в том, что статические экстремальные характеристики моделей сдвинуты относительно действительной характеристики объекта регулирования. На модели воздействуют те же возмущения, что и на объект; поэтому при перемещении характеристики объекта в плоскости x характеристики моделей будут также

перемещаться, не изменяя положения как относительно характеристики объекта, так и относительно друг друга.

Датчики, установленные на каждой модели, измеряют показатели экстремума 1' и 2' . Показания датчиков

подаются на устройство вычитания дифференциального регулятора, а результат вычитания — на усилитель. Дифференциальный регулятор поддерживает равенство

значении регулирующего воздействия x3 (рис. 3.1, б), которое

соответствует экстремуму реальной характеристики объекта регулирования. Таким образом, управляющее воздействие в рассматриваемой системе формируется в зависимости от величины и знака разности показателей качества моделей и удерживает систему в точке пересечения их характеристик, тем самым поддерживая показатель качества объекта в экстремуме. В данном случае поиск из области времени переносится в область пространства, т. е. определяются сразу две точки экстремальной характеристики.

Часто роль нелинейной части объекта в системе экстремального регулирования выполняют датчики. Это бывает тогда, когда экстремальное показание датчика соответствует оптимальному протеканию регулируемого про-

236

цесса. В этом случае для смещения экстремальной характеристики достаточно на вход датчика подавать постоянную во времени величину x . Кроме того, часто несколько объектов регулирования работает параллельно. Если на вход одного из объектов с экстремальной характеристикой подавать постоянную величину x , то его характеристика сдвинется в плоскости x в горизонтальном

направлении относительно характеристики другого объекта. Поэтому в обоих этих случаях можно применить описанную систему.

Подобные системы можно строить не только для объектов химического производства, но и для широкого круга объектов различной физической природы.

Для исследования системы, приведенной на рис. 3. 1, а, рассмотрим уравнения динамики ее элементов.

В дальнейшем будем исходить из предположения, что характеристика объекта регулирования достаточно точно аппроксимируется параболой следующего вида:

где ε — ошибка системы; θ — показатель качества; μ — регулирующее воздействие; λ — возмущение, перемещающее экстремальную характеристику объекта в плоскости , в

перемещающее экстремальную характеристику объекта в плоскости в вертикальном направлении, т. е. помеха.

Остальные звенья системы имеют следующее описание модели объекта

237

1 1 1[ a(x x )2 ] a 1 ( x)2 1

(3.2)

2 2 2 [ a(x x )2 ] a 2 ( x)2 2

238

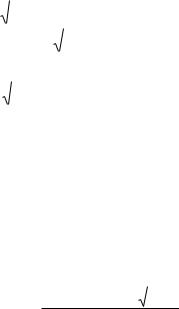
Закон регулирования

u= 3 . (3.6)

Известно, что ни в одной из поисковых экстремальных систем не удается получить такой закон регулирования, который при непрерывном изменении по произвольным законам λ (t) и λ′ (t) обеспечивал бы управление системой только в функции ее ошибки. Кроме ошибки системы в законе регулирования в этих условиях неизбежно присутствуют дополнительные (преимущественно нелинейные) члены, зависящие от вида функции λ′ (t). Это приводит к тому, что при определенном соотношении параметров системы, возмущений λ(t); λ(t) и начальных условий поисковая экстремальная система теряет способность отслеживать экстремум и становиться неработоспособным.

Подставив в закон регулирования (рис. 3.6) значения θ и θ , получим

u= 3a 2 2 1 2a 3 x 2 1

единственной из всех известных экстремальных систем без связи по возмущению , в которой при правильной настройке параметров управляющее воздействие зависит только от ошибки системы. Система абсолютно инвариантна к возмущению (т. е. к помехе).

Решая совместно уравнения элементов системы для ус239

тановившегося режима, можно получить выражение для ошибки системы в предположении, что 1 2 , а также исследовать влияние на ошибку системы изменения коэффициентов 1 и 2 и крутизны параболы a . Получены формулы для абсолютного и относительного изменения ошибки при вариации 1; 2 и a :

2 1 1 2 K a,

При несимметричной характеристике объекта сдвинутые характеристики моделей будут также несимметричны; в разных моделях они сдвигаются в разные стороны, поэтому точка их пересечения не будет соответствовать экстремуму характеристики объекта регулирования. Если предположить, что объект описывается уравнением

то ошибка, вызванная несимметричностью характеристик, будет равна

где

Предлагаемая система мало чем отличается от обычных линейных следящих систем; для исследования ее динамических свойств можно применить любые методы, пригодные для исследования линейных следящих систем.

Следует подчеркнуть, что дифференциальная система экстремального управления, использующая принцип сдвига характеристик, с успехом может решить и многопараметрические экстремальные задачи. В этом случае необходимо строить отдельные модели по всем регулирующим параметрам (рис. 3.2) точно так же, как и в системах с модулирующим воздействием необходимо иметь столько синхронных детекторов, сколько в многопараметрической системе имеется регулирующих параметров.

Пример. Пусть дано уравнение

Рис. 3.2 Функциональная схема многопараметрической дифференциальной системы экстремального управления, использующей принцип сдвига характеристик.

243

Это уравнение описывает в n -мерном пространстве поверхность второго порядка. Нас интересуют только такие функции , которые имеют либо экстремум-максимум, либо

экстремум-минимум. Для таких функций уравнение (3.14) представляет собой эллипсоид.

Необходимым условием экстремума дифференцируемой функции нескольких независимых переменных

является равенство нулю частных производных этой функции

Схеме, приведенной на рис. 3.2, соответствует следующая система уравнений;

245

n

Fm amm m xm 2 m xm amj j

i m

n

um Fm Fm 4amm m xm 4 xm amj j

j 1 j m

4 xm amj j ,

i1n

j 1

246

Если объект регулирования описывается уравнением, представляющим в n -мерном пространстве поверхность второго порядка с одни экстремумом, т. е. если выполняется условие, то система уравнений (3.24) будет справедливой только при нулевых значениях ошибки. Действительно, система уравнений (3.24) имеет m 20 единственное

решение, так как amj 0.. Во всех уравнениях этой системы свободный член равен нулю.

Таким образом, система, приведенная на рис. 3.3, в статических режимах будет всегда удерживать показатель качества в экстремуме, т. е. всегда будет ‚поддерживаться тождество

j 0, j 1,2,3,..., n,

где j — ошибка системы по соответствующей координате.

Как уже отмечалось, система с моделями сама по себе, без всяких дополнительных связей, абсолютно инвариантно к возмущениям , перемещающую экстремальную

характеристику объекта в вертикальном направлении (т. е. к помехе).

В линейных системах при определенных условиях можно не только добиться определенного минимума ошибки, но и обеспечить тождественное равенство ее нулю.

Из теории инвариантности известно, что в случае возможности измерения возмущений, действующих на линейную систему при определенных условиях, можно добиться инвариантности выходной

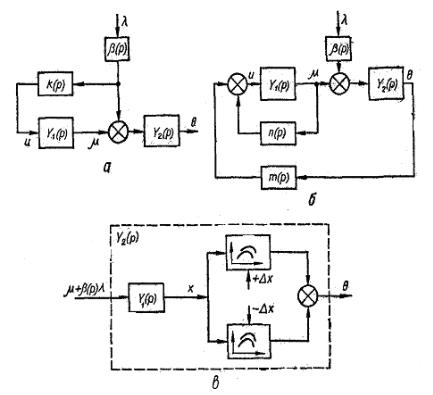
Рис. 3.З. Функциональныѐ схемы дифференциальных систем с моделями, в которых можно добиться инвариантности к возмущению:

а — система со связью по возмущению; б— система 6ез связи по возмущению;

в — развернутая схема звена с передаточной функцией Y2 p . ,

координаты системы к возмущениям. В экстремальных системах необходимо добиваться тождественного равенства нулю ошибки системы, т. е. тождества

где p — передаточная функция через которое возмущение действует на объект регулирования.

На рис. 3.3 приведены две дифференциальные системы экстремального управления с моделями нелинейной части объекта, в которых возможно добиться инвариантности к возмущению t . Система (рис. 3.3, а) представляет собой разомкнутую линейную систему с компаундирующей связью по возмущению t . Эта система описывается уравнениями.

получим

k p Y1 p 1 0,

т. е.

249

Это и будет условием абсолютной инвариантности для этой системы. В случае, если звено с передаточной функцией Y1 p обладает и инерционностью, то для обеспечения абсолютной инвариантности в этой системе необходимо создать звено с передаточной функцией k p, на выходе которого можно получить идеальные производные от возмущения t .

Как известно, реальные дифференциаторы никогда не дают чистой производной, и в случае инерционности звена Y1 p абсолютной инвариантности получить не удастся.

Нужно стремится как можно точнее выполнить условие (3.29), добиваясь максимального приближения системы к

абсолютной ее инвариантности по отношению к возмущению

t .

Особый интерес представляет собой система, приведенная на рис. 3.3,б, в которой отсутствует компаундирующая связь по возмущению. Эта система описывается следующими уравнениями.

Усилитель и сервомотор соответствуют (3.27). Объект соответствует (3.28).

250

Подставив найденное значение в общее условие

инвариантности для всех экстремальных систем (3.25), получим

m p Y1 p Y2 p 1 n p Y1 p m p Y1 p Y2 p 0. (3.32)

Из (3.32) видно, что условием абсолютной инвариантности рассматриваемой системы по отношению к возмущению будет

закон регулирования этой системы в принципе ничем не будет отличаться от закона регулирования системы, приведенной на рис. 3.3. а

Действительно, из (3.28) находим

Подставим это значение в закон регулирования (3.30)

u n p n p p Y2 p m p Y2 p . (3.36) Y2

Принимая во внимание (3.34), получим

251