
Основы математического анализа. учебное пособие для иностранных граждан - слушателей подготовительного отделения. Некрасова Н.Н., Горяйнов В.В
.pdf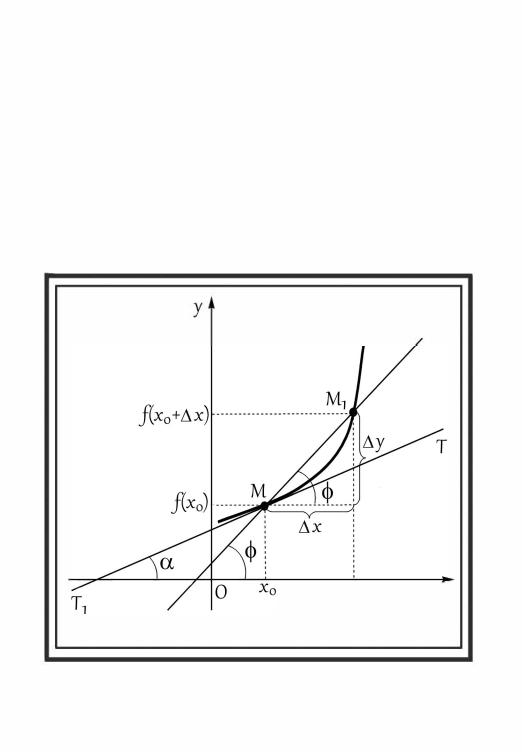
Н. Н. Некрасова, В. В. Горяйнов, А. Б. l(уев
основы
МАТЕМАТИ-ЧЕСl(ОГО АНАЛИЗА
y=f(x)
Хо+Лх х
Вороне>к 2020
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
Н. Н. Некрасова, В. В. Горяйнов, А. Б. Кущев
ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Учебное пособие
для иностранных граждан - слушателей подготовительного отделения
Воронеж 2020
УДК 517(075) ББК 22.161я73 Н48
Рецензенты:
кафедра математического моделирования Воронежского государственного университета (зав. кафедрой д-р физ.-мат., профессор В. А. Костин);
И. Ю. Покорная, канд. физ.-мат. наук, доц. кафедры высшей математики Воронежского государственного педагогического университета
Некрасова, Н. Н.
Основы математического анализа: учебное пособие для иностран-
ных граждан - слушателей подготовительного отделения / Н. Н. НекраН48 сова, В. В. Горяйнов, А. Б. Кущев; ФГБОУ ВО «Воронежский государственный технический университет». – Воронеж: Изд-во ВГТУ. – 2020.
– 125 с.
ISBN 978-5-7731-0859-7
Учебное пособие содержит сведения по основным разделам математического анализа. Материал сгруппирован по темам, содержит теоретические данные, которые сопровождаются набором примеров и задач с подробным решением. По каждой теме приводятся задачи для самостоятельного решения.
Предназначено для вводного адаптационного этапа преподавания математики на русском языке для иностранных учащихся подготовительного отделения.
Ил. 30 . Табл. 2. Библиогр.: 9 назв.
УДК 517(075) ББК 22.161я73
Печатается по решению редакцилонно-издательского совета Воронежского государственного технического университета
ISBN 978-5-7731-0859-7 |
© Некрасова Н. Н., Горяйнов В. В., |
|
Кущев А. Б. 2020 |
|
© ФГБОУ ВО «Воронежский |
|
государственный технический |
|
университет», 2020 |
2
ОГЛАВЛЕНИЕ |
|
ВВЕДЕНИЕ……………………….…………………………………… |
5 |
1. ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ… |
6 |
1.1. Понятие функции………………………………………………. |
6 |
1.2. Основные элементарные функции.............................................. |
13 |
1.3. Нахождение области определения функции………………….. |
19 |
1.4. Задания для самостоятельной работы ………………………... |
20 |
2. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ ………………………….. |
24 |
2.1. Бесконечные числовые последовательности ………………… |
24 |
2.2.Предел последовательности…………...………………………. 29
2.3.Бесконечно малые и бесконечно большие последовательно-
сти…………………………………………………. 34
2.4.Свойства пределов последовательности……………...………. 39
2.5.Монотонные последовательности…………………………….. 41
2.6. Задания для самостоятельной работы………………………… 46
3. ПРЕДЕЛ ФУНКЦИИ………………………………………………. |
50 |
3.1. Определение предела функции………………………………. |
50 |
3.2. Бесконечно малые функции………………………………….. |
53 |
3.3. Свойства пределов……………………………………………. |
55 |
3.4. Предел функции при x бесконечный предел функции. |
60 |
3.5. Задания для самостоятельной работы…………………….…... |
61 |
4. НЕПРЕРЫВНЫЕ ФУНКЦИ………………………………………. |
63 |
4.1. Определение непрерывности функции………………………. |
63 |
4.2. Теоремы о непрерывных функциях…………………………… |
65 |
4.3. Непрерывность элементарных функций……………............... |
67 |
4.4. Свойства функций, непрерывных на отрезке a,b ………….. |
70 |
4.5. Задания для самостоятельной работы ………………...……… |
72 |
5.ПРОИЗВОДНАЯ И ЕЁ ПРИМЕНЕНИЕ К ИССЛЕДОВАНИЮ ФУНКЦИИ…………………………………. 73
5.1. Определение производной…………………………………….. |
73 |
5.2. Теоремы о дифференцируемых функциях…………………… |
75 |
5.3. Производная обратной функции. Производная сложной |
80 |
функции………………………………………………………… |
|
5.4. Производные элементарных функций……………………….. |
82 |
5.5. Таблица производных и правила дифференцирования……... |
85 |
5.6. Механический смысл производной…………………………... |
86 |
5.7. Геометрический смысл производной………………………… |
88 |
3
5.8.Применение производной для построения графиков
функций………………………………………………………… 90
5.9.Применение производной к приближенным вычислениям.
Дифференциал…………………………………………………. 94
5.10.Геометрический смысл дифференциала……………………. 96
5. 11. Задания для самостоятельной работы……………………... |
97 |
6. ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ …………………………….. |
99 |
6.1. Первообразная и неопределенный интеграл ………………... |
99 |
6.2. Свойства неопределенного интеграла ………………………. |
102 |
6.3. Основные табличные интегралы……………………………… |
102 |
6.4. Основные методы интегрирования…………………………… |
104 |
6.5.Определенный интеграл ………………………………………. 108
6.6.Использование определенного интеграла для некоторых
задач механики…………………………………………………. 109
6.7.Геометрический смысл определенного интеграла …………. 111
6.8.Свойства определенного интеграла………………………….. 113
6.9. Задания для самостоятельной работы……………………..... |
115 |
7. ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ ДЛЯ АУДИТОРНОЙ И |
116 |
САМОСТОЯТЕЛЬНОЙ РАБОТЫ……………………………… |
|
Заключение……………………………………………………………. |
124 |
Библиографический список…………………..…………………….. |
124 |
4
ВВЕДЕНИЕ
Настоящее издание предназначено для иностранных граждан, слушателей подготовительного отделения института международного образования Воронежского государственного технического университета. Необходимость его создания обусловлена неоднородностью математической и языковой подготовки, полученной иностранными гражданами на родине.
В пособии используются основные лексикограмматические единицы, а также языковые штампы, характерные для языка математики. Широко используется международный символический язык математики: обозначения, рисунки, таблицы и так далее. Посредством знакомой учащимся математической символики создается смысловая опора, облегчающая понимание и усвоение материала. Математический анализ ‒ важнейшая часть курса математики, в которой изучаются переменные величины в их взаимосвязи. Овладение его основными понятиями: функции, предела и непрерывности, производной и дифференциала, неопределенного и определенного интегралов - требует настойчивости, терпения и, главное, упорного труда.
Пособие содержит необходимый материал по курсу «Основы математического анализа» и состоит из 7 разделов. Первые шесть разделов пособия начинаются с необходимого теоретического минимума, включающего важнейшие определения, теоремы и формулы. Затем подробно разбираются типовые задачи, после чего предлагаются для самостоятельного решения (дома или в аудитории) аналогичные задачи. В последнем разделе приводятся одни задачи по всему курсу.
Порядок рассматриваемых тем не является обязательным и по желанию преподавателя может быть изменен. Материал изложен в сжатой форме, поскольку работа с пособием рассчитана на последние два месяца обучения учащихся на подготовительном отделении. В основу структуры пособия положен принцип компактности, доступности и наглядности изучаемого материала.
Предлагаемое учебное пособие поможет иностранным учащимся в подготовке к сдаче экзамена по математике первого сертификационного уровня, а также при дальнейшем обучении в вузе.
Все приведенные в пособии иллюстрации выполнены авторами.
5
1. ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
1.1. Понятие функции
При рассмотрении количественных соотношений реального мира приходится сталкиваться с численными значениями различных геометрических, физических и других величин, как, например, времени, температуры, объема, длины, давления, плотности и т. д.
В зависимости от рассматриваемых условий одни из величин имеют постоянные численные значения, у других эти значения меняются. Такие величины называются соответственно постоянными и переменными. Существуют величины, сохраняющие постоянные числовые значения независимо от условий задачи, например величина прямого угла, атомная масса элемента и другие. Такие величины называют абсолютными постоянными.
Изучение окружающих нас явлений показывает, что переменные величины часто изменяются независимо друг от друга, а так как изменение численных значений одних из этих величин влечет за собой изменение значений других, то здесь будут рассматриваться лишь пары переменных, значения одной (зависимой) из которых изменяются в зависимости от значений другой (независимой). При этом в рассматриваемую зависимость двух переменных величин, кроме этих переменных, могут входить и некоторые постоянные величины, которые называют константами.
В данном пособии будем рассматривать зависимость пар переменных, когда независимой переменной или аргументу x, соответствует только одно значение зависимой переменной, или функции y. Такие функции называются од-
нозначными.
Определение 1.1. Соответствие между множествами X и Y , при котором каждому элементу x X соответствует один и только один элемент y Y,
называется функцией.
Множество X , при котором функция существует, называется областью определения функции.
Элемент y Y, соответствующий элементу x X , обозначают f x . Множество всех элементов f x  x X называется множеством значений
x X называется множеством значений
функции. Это множество является подмножеством множества |
Y , то есть |
f x x X Y . |
|
На рис. 1.1 областью определения функции y f x является множество |
|
чисел 1,2,3 , а множеством значений функции – множество чисел |
15,20 . |
6

1 |
15 |
25 |
|
3 |
2 |
30 |
|
20 |
40 |
||
|
Рис. 1.1. Иллюстрация области определения и области значения функции
Элементами множеств X и Y могут быть объекты любой природы, в частности, ими могут быть действительные числа. В этом случае мы имеем чи-
словую функцию y f x . Областью определения числовой функции могут быть как конечные, так и бесконечные числовые множества, прежде всего числовые промежутки. Основными из них являются интервалы a,b множество
таких x, что a |
x |
b, и отрезки a,b , когда a x b. Есть еще два типа |
промежутков: a,b |
и |
a,b (для квадратной скобки соответствующая гранич- |
ная точка входит в промежуток, а для круглой ‒ соответственно нет). В классическом анализе рассматриваются функции, заданные на промежутке или на
объединении промежутков. В случае промежутка |
, |
принято писать |
x R.
Ниже мы будем рассматривать только числовые функции, поэтому слово “числовые” можно опустить.
Замечание. Для произвольных множеств вместо слова “функция” часто используют термин “отображение”. Например, если каждому треугольнику ставить в соответствие вписанную в него окружность, то мы получаем отображение множества треугольников на множество окружностей.
В определении функции ничего не сказано о том, как задается соответствие между числами x и y. В зависимости от того, как задано это соответствие,
различают три основных способа задания функции.
Функцию можно задать с помощью формул (аналитически), например:
1)y 2x 1, x R;
2)y x – целая часть числа х, причем х п на числовом промежутке
п; п 1 , где п Z.
Чаще |
всего |
функцию задают с помощью одной формулы: |
y f (x) (x |
D |
R), но могут использоваться несколько функций, каждая из |
которых задается на своем промежутке, например:
y |
sinx, при x |
0, |
|
x2, при x |
0. |
|
7 |
|
В естественных науках и технике соответствие между величинами часто устанавливается экспериментально. Например, если подвергать газ давлению
Р 1; 2; 3; ...;10 |
атм. при постоянной температуре, то опытным путем можно |
||||||||||||
определить соответствующий каждому давлению объем газа V . В этом случае |
|||||||||||||
функция V(P) |
задается не формулой, а табл. 1. |
|
|
Таблица 1. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р, атм. |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
см3 |
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V8 |
V9 |
V10 |
|
Такой способ задания функции называется табличным.
В ряде случаев, особенно при использовании самопишущих приборов, функция задается непосредственно графиком. Такой способ задания функции y f x
называют графическим способом.
Определение 1.2. Графиком функции |
у f x называется множество |
|
точек координатной плоскости с координатами |
M(x; f (x)), x X. |
|
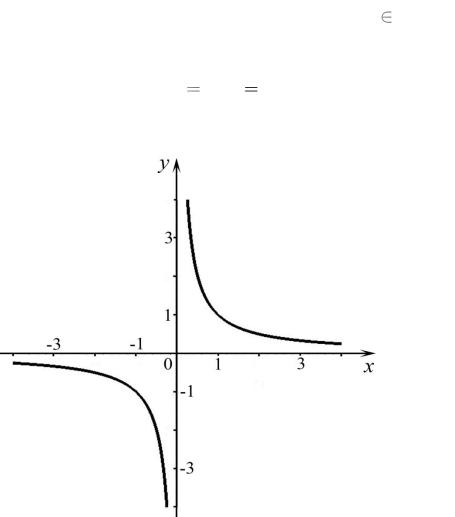
Например, на рис. |
1.2 изображено множество точек координатной плос- |
|
кости, соответствующих |
функции y f(x) |
1 . Соединив эти точки, полу- |
|
|
x |
чим график функции ‒ гиперболу.
Рис. 1.2. График функции у 1х
8

Замечание. Графическое задание функции является приближенным, потому что измерение отрезков производится с определенной точностью, но при этом обладает наглядностью.
Указанные выше три способа задания функции (аналитический, табличный и графический) являются наиболее употребительными, но не исчерпывают всех возможных способов. В частности, можно задать функцию подпрограммой для ЭВМ, с помощью которой вычисляются любые значения данной функции (сравните с табличным способом) или, наоборот, описав словами, какие значения она принимает для различных значений аргумента. Например, функция Ди-
рихле определяется следующим образом: f x равна нулю для всех рацио-
нальных значений x и равна единице для всех иррациональных значений x. Задание функции каким-либо способом не исключает возможности ее за-
дания и другими способами. Функцию Дирихле можно задать и аналитически:
y |
0, |
если x |
рациональное число, |
|
1, |
если x |
иррациональное число. |
Определение 1.3. Функция y f x , определенная на множестве X, называется ограниченной снизу, если существует число A такое, что A f x для любого х Х.
Функция y ax, ограничена снизу на всей области определения, так как ax 0 для любого действительного x.
Определение 1.4. Функция y f x , определенная на множестве X, называется ограниченной сверху, если существует число B такое, что f x B
для любого х Х. |
|
|||
Функция |
y |
1 x2 ограничена сверху на всей области существования, |
||
|
|
|
|
для любого x такого, что x 1;1 . |
так как 1 x2 |
1 |
|||
Определение 1.5. Функция y f x , определенная на множестве X, называется ограниченной, если существует число M 0 такое, что f x M для
любого х Х.
Например, функция y sinx ограничена на всей области определения, так как sinx 1 для любого действительного x.
Функция y f x , определенная на множестве X, ограничена на этом
множестве тогда и только тогда, когда она одновременно ограничена и снизу и сверху на этом множестве.
9
