
Методическое пособие 672
.pdf
является пересечением областей определений, входящих в выражение функций (при делении добавляется естественное ограничение, что знаменатель отличен от нуля);
2) для нахождения области определения сложной функции надо выписать область определения для внешней функции, решить полученное неравенство и взять пересечение его решения с областью определения внутренней функции.
Пример. Найти области определения функций:
y lnx arccosx; y |
1arcsin |
3x 1 |
; y |
log |
|
(2 |
|
. |
1 |
x) |
|||||||
|
x |
2 |
|
|
2 |
|
|
Решение. Для первой функции выпишем систему неравенств, составленную из областей определения входящих в формулу логарифмической и об-
ратной тригонометрической функций: |
|
x |
0, |
1. |
Тогда область определения |
|||||||||
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
||
функции есть x |
0,1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как для второй функции область определения |
arcsinz |
является отре- |
||||||||||||
зок z |
1,1 , то получим |
|
|
|
|
|
|
|
|
|
|
|||
1 |
3x 1 |
1, |
|
2 3x 1 2, |
|
|
|
1 3x 3, |
1 |
x 1, |
||||
x |
2 |
|
x |
0, |
|
|
|
x |
0, |
|
3 |
|
||
0, |
|
|
|
|
|
x |
0. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Область определения функции ‒ x |
1 |
,0 |
0,1 . |
|
|
|
|
|||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
Область определения внешней логарифмической функции для третьего |
||||||||||||||
примера являются положительные числа, тогда |
|
|
|
|
|
|||||||||
|
|
2 |
|
|
0, |
|
|
|
2, |
|
x |
4, |
|
|
|
|
|
x |
|
x |
|
|
|
||||||
|
|
x |
0, |
|
x |
0, |
|
|
x |
0, |
|
|
||
и областью определения является x |
0,4 . |
|
|
|
|
|
|
|||||||
1.4.Задания для самостоятельной работы
1.1.Вычислить:
1. f 0 , f 2 , f 3 , f 4 , если f x x2 5x 6.
2. f 1 , |
f 3 , |
f 4 , |
f 7 , если |
f x |
8 x |
. |
|
|
|
|
|
x |
|
20

|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3. |
f x , f |
|
x , |
f |
если f x x |
|
x 1. |
||||||||||||||||||
|
|
|
, |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
1 x |
|
|
|
|
|
||||
4. |
f 0 , |
f x |
, f |
5 |
|
если f x |
. |
|
|
|
|
||||||||||||||
|
|
|
, |
1 x |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||
5. |
f x 1 , |
f x 1, |
|
|
1 |
, |
если |
f x |
1 x. |
|
|||||||||||||||
|
f |
x |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|||||
6. |
f 2 , |
f 0 , |
|
f 1 , |
f 3 , |
если |
f x |
|
x, |
|
|
x 0, |
|||||||||||||
|
|
|
|
2, x 0. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x, |
|
x 1, |
|
7. |
f 3 , |
f 0 , |
|
|
|
, |
f 4 , если |
f x |
|
|
|
3 |
, |
1 x 1, |
|||||||||||
f |
2 |
|
x |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5, |
|
x 1. |
|||
|
f 0 , |
f 1 , |
f 5 , |
|
|
|
f x |
|
|
|
|
|
|
|
|
|
|||||||||
8. |
если |
|
|
. |
|
|
|
||||||||||||||||||
|
5 4x |
|
|
|
|||||||||||||||||||||
9. |
|
|
|
|
, f , если f x sinx. |
|
|
|
|
|
|
|
|||||||||||||
f |
, f |
4 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10. |
f (1), |
f (0,5), f (8), |
если |
f (x) |
|
|
log2 x. |
|
|
|
|||||||||||||||
1.2. Найти область определения функций:
1. y |
5 |
. |
2. y |
2 |
|
3 |
. |
3. y |
|
. |
|
x 2 |
|||||||||||
x 2 |
x |
x 4 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5. |
y |
|
|
1 |
|
|
|
. |
6. |
y lg x 7 . |
||
4. |
y 3 1 x . |
|
|
|
|
|||||||||||
log5 |
x 6 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
y 1 |
|
x 1 |
|
|
|
|
|
|
|||
7. |
y arcsin 5x 1 . |
8. |
|
x 1 |
|
. |
|
|
9. |
|||||||
|
|
|
|
y tg x |
. |
|||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
6 |
|
10.y x2 10x 24 .
1.3.Что означает:
функция ограничена сверху (снизу);
функция не является ограниченной сверху (снизу);
функция ограничена;
функция не является ограниченной;
функция периодическая;
функция не является периодической.
21

1.4. Исследовать функцию на четность (нечетность):
1. |
y 3x. |
2. |
y 3x2 2 . |
|||||||||||||||
4. |
y 2x tgx . |
|
|
|
|
|||||||||||||
5. |
y |
x4 1. |
||||||||||||||||
7. |
y |
|
x |
|
x. |
8.y sinx tgx. |
||||||||||||
|
|
|||||||||||||||||
10. |
y arcsinx arctgx. |
11. y ln 5x . |
||||||||||||||||
13. |
y |
|
x 2 |
|
|
|
x 2 |
|
. |
14.y 5x2 x4 . |
||||||||
|
|
|
|
|||||||||||||||
1.5. Определить период функции:
3. y 3x x4 .
6. y x5 3x 1.
9.y sin2x cos5x.
|
|
2 x |
|
12. |
y lg |
|
. |
|
|||
|
|
2 x |
|
15. |
y x12 |
cos5x. |
|
1. |
y cos3x. |
|
|
2. |
y sin |
x. |
|
3. |
y tg |
|
|
|
x . |
|
||||
|
|
|
|
3 |
|
|||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
x |
|
|
|
|
||
4. |
y 5sin3x . |
|
|
5. |
y cos5x cos10x. |
6. |
y cos |
. |
|
|
||||||||
|
|
2 |
|
|
||||||||||||||
|
|
|
|
|
x |
|
|
|
|
5x |
|
|
||||||
7. |
y cos 2x |
|
. |
8. |
y sin |
|
|
|
|
. |
9. |
y tg |
|
|
|
|
3 |
. |
3 |
2 |
3 |
|
|||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||
10.y cos26x.
1.6.Для заданной функции найти обратную функцию:
1. |
y 4x 5. |
2. |
y |
5 |
. |
3. |
y |
|
. |
|||
x |
||||||||||||
x 5 |
||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
||
4. |
y lg |
. |
5. |
y 8x 2. |
|
6. |
y 2sin7x. |
|||||
|
|
|||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
||
7. |
y x2 . |
8. |
y sinx. |
9. |
y logx 9. |
|||||||
10.y 3 1 x3 .
1 x3 .
1.7.В одной и той же системе координат построить график указанных групп функций и выяснить их взаимное расположение:
1. y x, y x2 ,y x3 , y x4 , y x5 .
22

2.y x, y arcsinx.
3.y x, y arctgx .
4. y x, y 
 x, y 3
x, y 3 x, y 4
x, y 4 x, y 5
x, y 5 x. 5. y x 2 , y cosx.
x. 5. y x 2 , y cosx.
1.8. Построить график следующих функций:
1. y x 1.
4. y 3x .
7. y x 2 2 4.
10. y 
 x 2.
x 2.
13. y 1x 2.
16. y x 2.
19. y cos2x .
x2 2x, x 1,
22. y
4 x, x 1.
2x, x 1,
1
25. y x, 1 x 0,
x2, x 0.
2. y x 2.
5. y 3x2 .
8. y x2 4x.
11. y x3 1.
14. y x 2 .
17. y x2 2x 8 .
20. y log1 x .
2
1, x 1,
23. y 2 x2, x 1,x, x 1.
3. y 2x 2.
6. y x2.
9. y 3x2 8x 3.
12. y 21x .
15. y 4x 2 .
18. y x2 2 x 8.
yx, x 0,
21.2 x, x 0.
x, x 0,
24. y cosx, 0 x 2 ,
tgx, x .
2
23

2. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
2.1.Бесконечные числовые последовательности
Бесконечные числовые последовательности (далее мы будем называть их просто последовательностями) образуются так: каждому числу п натурального ряда чисел
1, 2, … п,…
ставится в соответствие определенное действительное число хп и эти числа располагаются в порядке возрастания номеров п:
x1, x2,x3,...,xn,....
Такое соответствие есть функция. Множество натуральных чисел N является областью определения этой функции, а ее значения принадлежат множеству действительных чисел R.
Примерами последовательностей являются арифметическая прогрессия
1; 3; 5; 7; 9;… .
которая задается так:
x1 1, xn xn 1 2, n N,
и геометрическая прогрессия
1, 2, 4, 8, 16, …,
которая задается так:
x1 1, xn 2xn 1, n N.
Определение 2.1. Последовательностью называется числовая функция, определенная на множестве N натуральных чисел.
Числа xn называются членами последовательности.
Последовательность
x1, x2,x3,...,xn,...
сокращенно будем обозначать символом Хп . Формула, определяющая xn в
зависимости от п, называется формулой общего члена последовательности.
24

Пример. Даны последовательности, заданные общим членом. Выписать некоторые члены последовательности.
Решение.
С помощью формулы общего члена можно вычислить любой член последовательности:
1) xn 1n,
x1 1, x2 12, x3 13,...,x10 101 ,...,x127 1271 ;
2) x |
n |
|
, |
|
n |
1 |
|||
n |
|
x1 12, x2 23, x3 43,...,x23 2423,...,x243 244243;
3) xn 3,
в данной последовательности все члены одинаковы и равны числу 3:
|
|
x1 |
3, |
x2 |
3, x3 |
3,...,x47 |
3,...,x191 3. |
Определение 2.2. Суммой последовательностей |
|||||||
и |
|
|
|
xn |
(x1, x2,x3,...,xn,...) |
||
|
|
|
yn |
(y1, y2,y3,...,yn,...) |
|||
|
|
|
|
||||
называется последовательность |
|
|
|
||||
|
xn |
yn |
|
(x1 y1, x2 y2,x3 y3,...,xn yn,...); |
|||
разностью xn |
и yn |
называется последовательность |
|||||
|
xn |
yn |
|
(x1 |
y1, x2 |
y2,x3 |
y3,...,xn yn,...); |
произведением xn |
и |
yn называется последовательность |
|||||
|
|
xn |
yn |
(x1 y1, x2 y2,x3 |
y3,...,xn yn,...); |
||
частным xn |
и yn называется последовательность |
||||||
25
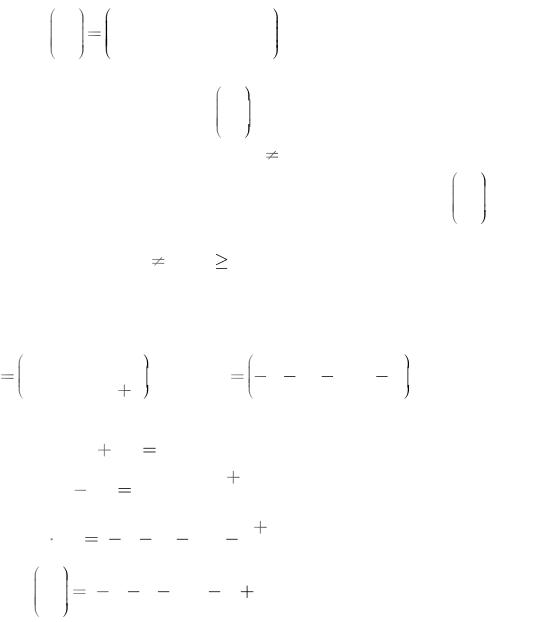
|
|
|
|
xn |
|
|
|
|
x1 |
|
, |
|
x2 |
, |
|
x3 |
,..., |
xn |
,... . |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
y |
n |
|
|
|
|
|
|
y |
2 |
|
|
y |
3 |
|
|
|
y |
n |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Замечание. |
При определении частного |
|
xn |
|
|
для всех элементов последо- |
||||||||||||||||||||||||||||
|
yn |
|
|
|||||||||||||||||||||||||||||||
вательности yn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
должно выполняться условие |
|
yn |
0. Если у последователь- |
|||||||||||||||||||||||||||||||
ности yn только конечное число элементов равно нулю, то частное |
xn |
|
||||||||||||||||||||||||||||||||
yn |
||||||||||||||||||||||||||||||||||
можно определить с того номера k, начиная с которого все элементы |
||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn |
|
|
0 |
|
|
(n k). |
|
|
|
|
|
|||||||||
Пример. Найдем сумму, разность, произведение и частное последова- |
||||||||||||||||||||||||||||||||||
тельностей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2, 3 |
, 4 |
,..., |
|
|
n |
|
|
|
|
и |
|
|
y |
n |
|
|
|
1, 1, |
1,..., |
1 . |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
n |
4 |
3 |
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
3 |
n |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Решение. |
|
|
|
|
|
|
|
xn |
|
|
|
yn |
|
|
|
(1,1,1,...,1,...); |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
x |
|
|
y |
n |
|
|
|
(3,2,5 |
,...,n |
2,...); |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||||||
|
x |
|
y |
n |
|
( |
2, |
|
3, |
|
4..., |
|
|
1,...); |
|
|
|
|
||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
9 |
|
|
|
|
|
n2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
xn |
|
|
|
( |
|
|
2, |
|
3, |
|
4,..., |
(n |
1),...). |
|
|
|
|
|||||||||||||||
|
|
yn |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Как и все функции, любую последовательность Хп можно изобразить графически на координатной плоскости точками
(1, x1),(2,x2),(3,x3),...,(n, xn),....
Это множество точек называется графиком последовательности xn . Можно также изобразить члены последовательности xn точками на числовой прямой, отмечая их соответствующими символами
x1, x2,x3,...,xn,...
На рис. 2.1, а, б приведены два описанных выше способа изображения
26

последовательности x |
n |
, заданной формулой x |
6. |
|
|
n n |
xn
6 

5
4
3
2
1
0 1 2 3 4 5 6 7 8 9 10 n
а)
|
x6 x5 x4 |
x3 |
x2 |
|
|
x1 |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
х |
б)
Рис. 2.1. Изображение последовательности Хп п6 : а) графически; б) точками на числовой прямой
Пример. Изобразить последовательность xn |
( 1)n |
на координатной |
плоскости и точками на числовой прямой. |
n |
|
|
|
Изображения данной последовательности приведены на рис. 2.2. Различные масштабы взяты для удобства. Пунктирные линии к графику не относятся и являются вспомогательными.
27

xп
1
0 |
1 |
2 |
3 4 |
5 |
6 |
7 |
8 |
n |
-1 |
|
|
|
|
|
|
|
|
а)
x1 |
x3 |
x5 x7 |
x6 x4 |
x2 |
|
|
-1 |
|
|
0 |
|
1 |
x |
|
|
|
б) |
|
|
|
|
Рис. 2.2. Графическое изображение последовательности xn |
( 1)n |
: |
|||
|
а) графически; б) точками на числовой прямой |
n |
|
|||
|
|
|
||||
Определение 2.3. Последовательность xn |
называется |
ограниченной, |
||||
если существуют такие два числа M и т, что для всех п выполняется двойное неравенство
mxn M .
Пример. Является ли данные последовательности ограниченными?
1. xn n2n1.
Так как
xn 1 n2n1 1 nn 11 0;
и
28

xn 2 n2n1 2 n 21 0,
то при всех n выполняется неравенство
1xn 2.
Следовательно, данная последовательность ограничена.
2. |
xn |
( |
1)n |
‒ эта последовательность ограничена, так как для всех n |
|||
|
|
|
n |
|
|
|
|
выполняется неравенство |
( 1)n |
|
|||||
|
|
|
|
|
1 |
1. |
|
|
|
|
|
|
n |
||
|
|
n |
2 |
|
|
|
|
3. |
xn |
|
‒ эта последовательность не является ограниченной. |
||||
|
5 |
|
|||||
|
|
|
|
|
|
|
|
Так как какое бы большее число M мы ни взяли, всегда найдется такое натуральное число N 5M , что для всех n N выполняется
xn |
n 2 |
N 2 |
|
N |
M , |
|
5 |
5 |
5 |
||||
|
|
|||||
то есть
xn M .
2.2. Предел последовательности
Определение 2.4. Число a называется |
пределом последовательности |
xn , если для любого положительного числа |
найдется такое натуральное |
число N, что при всех n N выполняется неравенство xn a ε.
В этом случае говорят, что последовательность xn имеет пределом число a и пишут:
limn xn a,
или говорят, что последовательность сходится к a, и пишут: xn a при n .
Замечание. Число N в определении 2.4 последовательности зависит как
29
