Методическое пособие 672

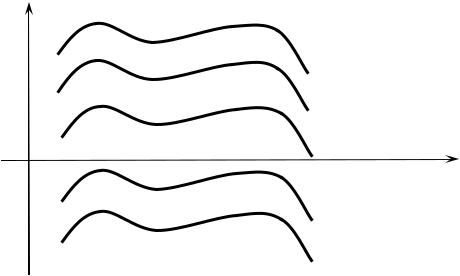
для всех x X . Следовательно, по определению 6.1 функция x F x C является первообразной для f x .

Докажем второе утверждение. Пусть F x и x − первообразные для f x при всех x X , то есть F x f x и x f x для всех x X .

Рассмотрим производную разности x F x :

x F x x F x f x f x 0.

Отсюда по теореме 5.4 следует:

x F x C, где C const

или

x F x C.

интегральной кривой (рис. 6.1).

у

100

Решение. Согласно теореме 6.1, любую первообразную функции y x2

гласно теореме 6.1

f x dx F x C; C R.

Отметим, что операция интегрирования является обратной к операции дифференцирования и, как это обычно бывает для обратных операций, намного сложнее и даже выводит за рамки элементарных функций.

Всякая непрерывная на (a,b) функция имеет на этом промежутке первообразную, а следовательно, и неопределенный интеграл.

101

6.2. Свойства неопределенного интеграла

Отметим ряд свойств неопределенного интеграла, вытекающих из его определения.

1. Производная неопределенного интеграла равна подынтегральной функции, а дифференциал ‒ подынтегральному выражению:

Доказательство этого свойства следует из определения неопределенного интеграла.

2.Неопределенный интеграл от дифференциала некоторой функции равен сумме самой этой функции и константы:

d( f x ) f x С .

3.Постоянный множитель можно выносить за знак интеграла:

af x dx a f x dx, где а const.

4. Неопределенный интеграл от алгебраической суммы (разности) конечного числа непрерывных функций равен сумме (разности) интегралов от слагаемых функций, в частности для двух функций

f x g x dx f x dx g x dx.

5. Если f x dx F x C, то и f u du F u C, где

u x (x) произвольная функция, имеющая непрерывную производную.

Таким образом, формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.

6.3. Основные табличные интегралы

Пользуясь определением 6.2 и правилами дифференцирования, выпишем основные табличные интегралы:

1) dx x C;

102

xn 1

2)xndx n 1 C n 1 ;

5)exdx ex C ;

6)sinxdx cosx C ;

7)cosxdx sinx C;

8)cosdx2 x tgx C;

9)sindx2 x ctg x C;

ветствующих функций.

Для примера докажем формулу (3) из табличных интегралов. При x 0, по определению, x x и

ln x lnx 1x .

Если x 0, то x x и

ln x ln x 1 1 .1 x

Таким образом формула (3) доказана для всех x 0.

Отметим, что во всех интегралах, где внешней функцией первообразной является натуральный логарифм, необходимо выражение внутри логарифма

103

брать по модулю, чтобы не терять часть области определения подынтегральной функции.

Остальные формулы таблицы доказываются аналогично непосредственной проверкой.

6.4. Основные методы интегрирования

Рассмотрим три основных метода интегрирования: 1. Непосредственное интегрирование.

Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам. Таких функций очень мало, одним из возможных подклассов этих функций являются многочлены. Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную, очень мало.

Метод внесения под знак дифференциала

дынтегральную функцию.

Отметим, что данный пример показывает, что при интегрировании мы делаем операции, обратные операциям при дифференцировании сложной функции: так сначала бралась производная от внешней показательной функции

ez , а затем от внутренней тригонометрической функции z sinx. А при интегрировании методом внесения под знак дифференциала мы сначала интегрируем тригонометрическую функцию, внося е под знак дифференциала, а на втором

шаге используем табличный интеграл от ez .

При сведении интеграла к табличному часто используются следующие преобразования дифференциала (операция «подведения или внесения под знак дифференциала»):

104

и так далее.

Примеры

2. Способ подстановки (замены переменных).

Если требуется вычислить интеграл f (x)dx , но сложно отыскать

первообразную, то с помощью замены x (t), где (t) функция, имеющая непрерывную производную и dx (t)dt , получаем формулу интегрирования подстановкой:

f x dx f t t dt.

Примеры

105

ex4dx 4 etdt 4et C 4ex4 C;

Замечание. Данный интеграл проще проинтегрировать методом внесения под знак дифференциала.

3. Интегрирование по частям.

Пусть u u(x) и v v(x) функции, имеющие непрерывные

производные. Способ основан на известной формуле производной произведения:

(u v) u v u v .

В дифференциальной форме: d(uv) udv vdu.

Проинтегрировав последнее равенство, получаем

d(uv) udv vdu,

ав соответствии с приведенными выше свойствами неопределенного интеграла:

uv udv vdu

или

106

Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.

Замечание. Функция u u(x) в формуле (6.1) дифференцируется, функция v v(x) интегрируется, поэтому при выборе u выбирают ту функцию, которая сильно упрощается при дифференцировании.

Примеры

Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить подынтегральную функцию и привести интеграл к табличному.

107

Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства:

6.5. Определенный интеграл

Определение 6.3. Определенным интегралом от a до b функции f x называется приращение первообразной F x этой функции:

F b F a .

Определенный интеграл обозначается так:

b f x dx F b F a ( Формула Ньютона-Лейбница),

a

где число a называется нижним пределом интегрирования, число b ‒ верхним пределом интегрирования, отрезок a,b областью (отрезком интег-

рирования.

Можно доказать, что приращение первообразной F b F a зависит

108

только от заданной функции f x и чисел a и b. Действительно, пусть F x и

что и требовалось доказать

Замечание. Формулу Ньютона-Лейбница часто записывают в следующем

виде:

b

f x dx F x ba F b F a .

a

Отметим, что в классическом математическом анализе определенный интеграл Римана (как и вообще любой определенный интеграл) задается как предел интегральных сумм, а формула Ньютона-Лейбница позволяет вычислять его с помощью первообразных.

Пример. Вычислим интеграл

6.6. Использование определенного интеграла для некоторых задач механики

Пусть закон движения материальной точки вдоль оси OX задан функцией x x t , где t ‒ время. Известна скорость движения точки в каждый момент

времени t, то есть известна зависимость V V t . По определению скорости

V t0 limt xt .

0

Следовательно, функция x t является первообразной для функции V t . Тогда, если движение точки начинается с момента времени t t0 по формуле Ньютона-Лейбница имеем

109