Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методическое пособие 672

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

3.74 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1310 11 12 13 > Следующая >>>

Пример.		Найти	угловые		коэффициенты		касательных к параболе
y 2x2 2	в	точках,		абсциссы которых			соответственно		равны:
x1 1; x2 2; x3 0.
Решение.		Найдем производную функции y 2x2 2,
				y 2x2 2 4x.
Следовательно, при				x 1	угловой	коэффициент		касательной	равен
k y 1 4;	при x 2 имеем k y 2					и при	x 0	угловой коэффици-
ент касательной равен			k y 0 0.

5.8. Применение производной для построения графиков функции

Рассмотрим применение производной для нахождения экстремумов (минимумов и максимумов) функции.

Теорема 5.4. Признаки возрастания, убывания и постоянства функции.

Если функция

f x дифференцируема на интервале a;b и

f x 0

( f x 0)

для

x (a,b), то функция возрастает (убывает)

на интервале

a;b . Если

f x 0

на

интервале

a;b ,

то функция

постоянна

f x const .

f x0 0, то-

Докажем первое утверждение теоремы. Пусть, например,

гда из формулы (5.1) уравнения касательной

f x f x0 f x0 x x0 0

при x x0

f (x) f x0

при x x0 .

наоборот, f (x)

x0 0 при

x x0 , то есть

f (x) f x0

при x x0 .

Следовательно, в окрестности точки

x x0 функция

y f x

строго возрастает. Аналогично можно показать, что

функция будет убывать при

f x0 0.

Пример. Построим график функции y x2 x. Очевидно,

что эта функ-

ция определена на множестве

R. Пользуясь сформулированным признаком,

определим

интервалы возрастания и убывания этой функции. Найдем произ-

водную y 2x 1

и решим неравенство 2x 1 0. Отсюда следует, что y 0 в

в интервале

;

произ-

интервале

;

. В точке

водная равна нулю (рис. 5.4) и в этой точке функция имеет минимум.

у	y x2 x
f x 0	f x 0
2
1
0

		1		1	1		х
		1		1	1
				2
		Рис. 5.4. График функции y x2				x
Напомним, что точка x0			называется		точкой максимума (минимума)
функции y f x , если в некоторой е				f (x) f x0			( f (x) f x0 )	при
x x0 .
Теорема Ферма. Необходимое условие экстремума.
Если в точке x0 дифференцируемая функция						f x	имеет экстремум, то
f x0 0.
Доказательство. Для определенности будем считать, что в точке								x0
функция f x имеет максимум. Для доказательства воспользуемся методом от
противного.	f x0 0, тогда или		f x0 0,			f x0 0.
Пусть	f x0 0, тогда или		f x0 0,		или	f x0 0.
Если	f x0 0, то в силу теоремы 5.4 в окрестности точки x0 функция
f x возрастает, а если		f x0 0 ‒ то убывает,				но в обоих случаях экстре-

мума в точке x0 нет. Значит, наше предположение не верно и f x0 0.

Из теоремы Ферма следует правило нахождения тех значений из области определения функции f x , в которой данная функция может принимать мак-

симальное или минимальное значение:
1.	Находим производную функции f x ;
2.	Находим все решения уравнения f x 0;	f x на числовой
3.	Методом интервалов расставляем знаки функции y	f x на числовой
	прямой;
	91

4. Если производная меняет знак с ″+″ на ″ ″, то в данной точке f x

имеет максимум (рис. 5.5, а), а если с f x имеет минимум (рис. 5.5, б).

max f x f x0

f x0 0

О x0

а)

f x0 0

min f x f x0

″–″ на ″+″, то в данной точке

f x0 0

О	x0	х
б)
Рис. 5.5. Экстремумы функции		y f x :
а) x0 точка максимума; б)	x0 точка минимума

Замечание. Четвертый пункт станет понятен, если дать следующее определение: при переходе через точку максимума возрастание функции сменяется на убывание, а в точке минимума ‒ наоборот, убывание на возрастание.

Пример. Найти экстремумы функции

y 151 3x5 25x3 60x 16 .

Решение.

Вычислим производную

y 151 15x4 75x2 60 x4 5x2 4 x2 1 x2 4 .

Корнями	уравнения			y 0	являются		x1 2; x2	2;	x3 1; x4 1.
Эти значения x делят числовую ось OX на интервалы ; 2 ;									2; 1 ; 1;1 ;
1;2 ; 2; рис. 5.6. Определим знаки производной								y на каждом из этих
интервалов.
	+		‒		+		‒	+	х
3					0			3
						1	2
		2		1
		Рис. 5.6. Знаки производной				y	на интервалах

Следовательно, точки x2 2 и x3 1 есть точки максимума, а точки x4 1 и x1 2 ‒ точки минимума.

Пример. Найти интервалы возрастания и убывания функции, а также экстремумы функции y x2 2x 1.

Решение.

Вычислим производную

			y 2x 2.
y 0	при x 1,	y 0 при	x 1	и y 0 при	x 1. Следовательно, функ-
ция	y x2 2x 1 возрастает в			интервале ;1 и убывает в интервале

1; . В точке x 1 функция имеет максимум.

В рассмотренных выше примерах в точках экстремума (минимума и максимума) функции выполняется условие y 0. Отметим, что условие y 0 вы-

полняется не только в точках экстремума функции, но и в точках перегиба функции, в которых график функции переходит через касательную, при этом производная равна нулю, но знака не меняет.

Например, функция y x3

имеет производную y 3x2 . В точке x 0,

y 0, однако в этой точке нет ни минимума, ни максимума функции (рис. 5.7). Точка О 0;0 для функции y x3 является точкой перегиба.

Рис. 5.7. Точка x x0 ‒ точка перегиба

5.9. Применение производных к приближенным вычислениям. Дифференциал

Рассмотрим функцию y f x , дифференцируемую в точке x0


		f x0	lim	f		x f x0
						x x0
и введем обозначение			x x0
			f x f			x0
		x					f x0 .
			x x0

Тогда x по	теореме 3.2,		есть бесконечно малая функция в точке x0 :
x 0 при	x x0 или, что то же самое, при									x 0. Из этого следует,
что при малых x справедлива формула
		f x f x0			f x			f	x0

или		x x0				x
		f x f				x0 x.

Е часто используют для приближенных вычислений вместо точной формулы

где	f x f x0 x O x 2,				(5.2)
		O x x x.

Для второго слагаемого в правой части формулы (5.2) справедливо равен-
ство	O x		x x
lim		lim		lim x 0,
	x		x
x 0		x 0		x 0

поэтому эту часть приращения называют бесконечно малой более высокого порядка, чем x. Для всех бесконечно малых высших порядков, чем x, ис-

пользуют обозначение O x .

Выражение f (x) x называют главной линейной частью приращения

функции.

Определение 5.4. Дифференциалом функции y f x в точке x0 назы-

вается главная линейная часть ее приращения. Дифференциал равен произведению производной функции на приращение аргумента и обозначается dy

или df (x):

dy f (x) x.

Как видим, для любой дифференцируемой функции справедлива формула (5.2). Верно и обратное утверждение. Если приращение функции y f x в

точке x0 может быть представлено в виде

				f x a x O x,					(5.3)
где a не зависит от x, то производная f x в точке x0									существует и равна a:
					f x0 a.
Действительно, из (5.3)			следует, что
					f x	a x ,
						a x ,
					x
где x	O x	− бесконечно малая функция						при x x .
где x		− бесконечно малая функция						при x x .
	x								0
	x
Откуда по теореме 3.2			имеем				f x
			f	x0 lim			f x	a.
			f	x0 lim			x	a.
					x 0		x

2 читается: O малое от дельта икс

Практическое применение дифференциал находит в приближенных вычислениях. Для этого в приближенную формулу

f x f x0 f x f x0 x f x0 x x0

подставляют конкретные значения f x0 и f x0 .

Возьмем, например, x0 0, тогда для малых x (близких к 0) получим

f x f 0 f 0 x.

Подставляя в эту формулу вместо f x различные элементарные функции, получим ряд важных формул:

1 x n 1 n x, в частности для 1 x 1 12x; ex 1 x; ln 1 x x; sinx x; tgx x.

Отметим, что для тригонометрических функций x измеряется в радиа-

нах.

Аналогичные формулы можно получить для любой дифференцируемой функции.

Для примера сделаем следующие приближенные вычисления по приведенным формулам:

1 0,0023 3 1 3 0,0023 1,0069 ;

1 0,002 1 1 0,002 1,001	;
2
e0,0071 1 0,0071 1,0071 ;
ln 1 0,003 0,003 ;
sin0,0027 0,0027 ;
tg 0,0091 0,0091 .
5.10. Геометрический смысл дифференциала
Пусть y f x ‒ функция, которая имеет производную в точке		x x0 .

Зададим приращение аргумента x в точке x0 (рис. 5.8). Если M0T − касатель-

ная к графику функции y f x в точке M0(x0, f (x0), то tg f x0 . Из треугольника M0TP получим:

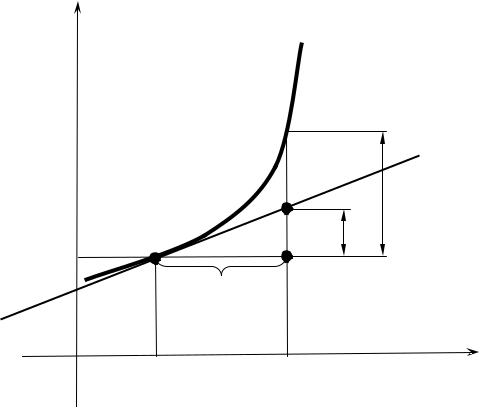
TP f x0 x dy.

Следовательно, величина дифференциала есть приращение ординаты касательной к графику функции в точке x0 x. Заметим, что приращение функции y

может быть больше dy, меньше dy или равно dy, но предел отношения разности y dy к x всегда стремится к нулю при x 0.

y f x

		y
		T
		dy
	y	М0
	y	P
		P
		x

О	x	0	x0 x	х
		0

Рис. 5.8. Графическая иллюстрация к определению дифференциала

5.11.Задания для самостоятельной работы

5.1.Используя определение производной, найдите производные данных

функций:

а) y x3 ;

б) y 1 ;

в)

5.2. Найдите производные заданных функций:

y x3 x2 ;

y x4 2x2;

7 x

;

3 x

y x2 1 ;

y 5x5

10x 2

;

1 3x6

;

2x 4

7) y	x3	;	8) y x3(6 x2);	9)	y (x4 5) (1	1).
	5 x2
						x

5.3. Напишите уравнение касательной для данных функций в указанных точках x0 :

1)	y x2 , x0 0, 1,1;						2)	y x3 , x0 2;
3)	y	2	, x	0	1,1	;	4)	y x2	1	, x	0	1.
		x		0					x		0

5.4. С помощью производной постройте графики данных функций:

1)	y x3 3x2 ;														2)	y	7 x				;
1)	y x3 3x2 ;														2)	y	3 x				;
																	3 x
3)	y x4 2x2										9;				4)	y	1 x sinx на							0, ;
		1			x4 13x3 36 ;												2
5)	y														6)	y			x 2x;
																		3
		10																3
7)	y x		2					2	;						8)	y sin			2	x		2cosx			1	.
7)	y x							x	;						8)	y sin				x		2cosx			4	.
								x																	4
	5.5. Найдите производные следующих функций:
1)	y 2x								10			;			2)	y sin3 2x;
1)	y 2x						3					;
3)	y log3(4x3 x2 7);														4)	S Asin						t	;
3)	y log3(4x3 x2 7);
5)	y 2x						3			5	7 x		4	;	6)	y tg2x 3 x 1 3;
5)	y 2x						3				7 x			;
															8)	y arccos(3x 5);
7)	y			x		2		1		;					8)	y arccos(3x 5);
						2

			x 3
			x 3
9)	y 5cos2x ln(7x 3);														10) y ex arcsin x 1 .
9)	y 5cos2x ln(7x 3);

6.ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ

6.1.Первообразная и неопределенный интеграл

Определение 6.1. Функция F x называется первообразной для функции f x на числовом промежутке X , если для всех x из этого промежутка выполняется равенство

F x f x .

Например, первообразной для

функции

f x x

является

функция

F x

, так как

1 2x x f x

F x

для всех x R.

Первообразной для

функции

f x

является

функция

1 x2

F(x) arcsinx, так как

x arcsinx

1 x2 ,

x 1,1 .

Сформулируем и докажем основное свойство первообразных.

Теорема 6.1. Если функция F x есть первообразная для функции f x на числовом промежутке X , то:

1)для любой постоянной C R функция

x F x C

также является первообразной для функции f x на числовом промежутке X

(без доказательства отметим, что верно и обратное утверждение);

2) любая первообразная для функции f x на числовом промежутке X может быть записана в виде: x F x C.

Доказательство. Докажем первое утверждение. Пусть F x − первообразная для f x , тогда

x F x C F x C F x 0 f x

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1310 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20223.71 Mб3Методическое пособие 669.pdf
#
30.04.2022730.62 Кб22Методическое пособие 67.doc
#
30.04.2022340.58 Кб6Методическое пособие 67.pdf
#
30.04.20223.72 Mб5Методическое пособие 670.pdf
#
30.04.20223.72 Mб7Методическое пособие 671.pdf
#
30.04.20223.74 Mб5Методическое пособие 672.pdf
#
30.04.20223.74 Mб1Методическое пособие 673.pdf
#
30.04.20223.79 Mб4Методическое пособие 674.pdf
#
30.04.20223.93 Mб5Методическое пособие 675.pdf
#
30.04.20223.93 Mб54Методическое пособие 676.pdf
#
30.04.20223.97 Mб4Методическое пособие 677.pdf