
Методическое пособие 672
.pdf
Пример. Найти производную функции |
f x |
1 x |
; |
x 1. |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x 1 x |
|
|
|
|
2 |
|
|
|||||||||||||||
x |
|
|
1 x 1 x 1 x 1 x |
|
|
|
|
|
. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
|
1 x |
2 |
|
|
|
|
|
|
|
1 x |
2 |
|
|
|
1 |
x |
2 |
|||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пример. Найти производную функции f x |
x2 1 |
; |
x 0. |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
2 |
|
1 |
|
x |
2 |
|
x |
2 |
|
|
|
|
2x |
2 |
x |
2 |
1 |
|
x |
2 |
1 |
|
|
|
|||||||||||
|
|
|
|
|
|
1 x |
|
1 x |
|
|
|
|
|
|
. |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
x |
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
5.3. Производная обратной функции. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Производная сложной функции |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Теорема 5.3. |
Пусть функция y f x |
удовлетворяет условиям теоремы |
||||||||||||||||||||||||||||||||||||
о существовании обратной функции (теорема 4.3) и в точке x имеет не равную
нулю производную y |
f x . Тогда для обратной функции x f 1 y в точке |
|||||||||
y0 f x0 также существует производная, равная |
|
|
||||||||
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
|
|
f x |
yx . |
||||||
|
xy |
|
f |
|
y |
|
||||
Доказательство. Придадим значению y f x произвольное прираще- |
||||||||||
ние y, тогда в точке x |
функция |
f 1 y |
получит соответствующее прираще- |
|||||||
ние x. При y 0 и x 0 имеем |
|
|
|
|
|
|||||
yx 1y .
x
Если теперь y 0, то в силу непрерывности обратной функции x f 1 y (теорема 4.3), приращение x 0. Тогда знаменатель в правой части равенства стремится к значению f x 0. Следовательно, существует предел и для левой части
80

|
|
lim |
x |
|
1 |
|
|
|
|
и x |
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
yx |
|
|
|
|
|
|
|||||||||||
|
|
y 0 |
y |
|
|
lim |
y |
|
y |
|
|
|
|
|
|
|
|
||||||||
или |
|
|
|
|
|
x 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
f x . |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример. Найти производную функции y arcsinx; 1 x 1. |
|
|
|||||||||||||||||||||||
Решение. Обратной данной будет функция |
x sin y |
|
|
|
y |
|
. |
||||||||||||||||||
По теореме 5.3 имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
yx arcsinx |
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||||
|
|
xy |
|
|
sin y |
cosy |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
Так как |
|
y , то |
cos y 0, |
|
поэтому |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos y 1 sin2 y  1 x2 .
1 x2 .
Следовательно,
|
|
|
arcsinx |
|
1 |
|
. |
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 x2 |
|
|||
Теорема 5.4. |
Пусть функция z g x имеет производную в точке x, а |
|||||||||
функция y f z |
имеет производную в точке z g x . Тогда сложная функ- |
|||||||||
ция y f g |
x также имеет производную в точке |
x, которая находится по |
||||||||
|
|
|
|
|
|
|
|
|
|
|
формуле |
|
|
|
|
|
или yx |
yz zx . |
|||
|
|
y f z |
|
z g(x) |
g x |
|||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Сформулируем словесное правило дифференцирования сложной функ-
ции: производная от сложной функции равна произведению производной внешней функции на производную от внутренней функции.
Эту теорему примем без доказательства.
Пример. Найти производную функции y 1 x2 100 .
Решение. Обозначим за z 1 x2 , тогда y z100 и по теореме 5.4 име-
ем
81

yx yz zx z100 z |
1 x2 x 100z99 |
|
z 1 x2 2x |
|
|||
|
z 1 x2 |
|
|
|
|
|
100 1 x2 99 2x 200x 1 x2 99 .
1 x2 100 200x 1 x2 99 .
Пример. Найти производную функции y sinx2 .
Решение. Обозначим за z x2, тогда y sinz и по теореме 5.4
yx yz zx sinz z x2 cosz z x2 2x 2xcosx2 ;
sinx2 2xcosx2 .
5.4.Производные элементарных функций
1.Целая рациональная функция (многочлен)
P x a xn a xn 1 |
a |
n 1 |
x a |
n |
; |
a 0. |
|
|
0 |
1 |
|
|
|
0 |
|
||
Из теоремы 5.2 следует, что многочлен |
P x |
есть дифференцируемая |
||||||
функция при всех x R и производная от многочлена имеет вид |
|
|||||||
P x a0xn a1xn 1 |
an 1x an na0xn 1 n 1 a1xn 2 |
an 1. |
||||||
2. Степенная функция
y xn .
Из примера и замечания п. 5.2 следует, что степенная функция есть дифференцируемая в своей области определения и
xn nxn 1. |
|
|
|
|
|
|
|
3. Логарифмическая и показательная функции |
|
|
|
|
|
|
|
В разделе 2 было доказано, что последовательность |
|
|
1 |
1 |
n |
имеет |
|
|
|
|
|
|
|||
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
предел, который обозначается буквой e:
82

|
|
|
|
1 n |
|
|
|
|
lim 1 |
n |
e. |
|
|
|
x |
|
|
По аналогии с этим утверждением без доказательства примем, что предел |
|||||
|
1 |
x |
при x существует и также равен e: |
||
функции f x 1 |
x |
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
lim 1 |
x |
x e. |
|
|
|
x |
|
|
Непосредственно из этого утверждения можно получить следующие два равенства:
1
lim 1 x x e;
x 0
limln 1 x 1.
x 0 x
C помощью этих равенств найдем производную логарифмической функции f x lnx:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
ln x x lnx |
|
|
|
|
|
ln 1 |
x |
|
|
|
1lim |
ln 1 t |
|
1 |
|
||||||||||||
|
lnx lim |
lim |
|
|
|
|
|
|
|
, |
||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
t |
x |
||||||||||||||||||||
|
|
x 0 |
x |
|
|
|
|
x 0 |
|
|
x |
|
|
|
|
x |
y 0 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||
где t |
x, |
при этом |
t 0 |
при |
x 0. То есть |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
lnx |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Далее |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lnx |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
lgx |
|
|
|
|
|
|
|
|
|
|
lnx |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ln10 |
xln10 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
ln10 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
и при 0 a 1 имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
lnx |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
loga x |
|
|
|
|
|
|
|
|
lnx |
|
|
|
|
|
. |
|
|
|
|
||||||||
|
|
|
|
lna |
|
|
xlna |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
lna |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Следовательно, логарифмическая функция есть дифференцируемая в своей области определения.
Для определения производной показательной функции используем теорему о производной обратной функции (теорему 5.3). Известно, что для функ-
ции y ax обратной является функция x loga y . Так как
83

|
x |
|
|
1 |
|
|
, |
|||
|
ylna |
|||||||||
то |
|
y |
|
|
|
|
|
|||
1 |
|
|
|
|
|
1 |
|
|
|
|
ax yx |
|
|
|
|
|
ylna ax lna |
||||
xy |
|
|
|
1 |
|
|||||
|
|
|
|
|
ylna |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
или
ax ax lna.
Вслучае, когда a e, эта формула имеет следующий вид:
ex ex.
Таким образом, показательная функция есть дифференцируемая в своей области определения R 0 a 1 .
4. Тригонометрические функции
В п. 5.1 было доказано, что функция y sinx дифференцируема при всех x R и
sinx cosx.
Найдем производную функции y cosx; x R. Так как
cosx sin 2 x ,
то обозначим
z 2 x.
По правилу дифференцирования сложной функции
y yz zx sinz z 2 x 2 x x cosz 2 x 1 cos 2 x cosx
или
cosx sinx.
84

Найдем |
производную |
функций |
|
y tgx; |
х |
|
k |
|
и |
|
y ctgx; |
||||||||||||||
x k k 0; 1; 2;... . |
По теореме 5.2 имеем |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
cosx cosx |
|
|
|
|
cos |
2 |
x sin |
2 |
x |
|
1 |
|
|
||||||||
|
sinx |
sinx |
sinx |
|
|
|
|
|
|
||||||||||||||||
tgx |
|
|
|
cos |
2 |
x |
|
|
|
|
|
|
cos |
2 |
x |
|
|
|
cos |
2 |
x |
||||
или |
cosx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
tgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Аналогично выведите, что ctgx |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, все тригонометрические функции дифференцируемы в своей области определения.
5. Обратные тригонометрические функции
arcsinx |
1 |
|
; |
arccosx |
|
|
1 |
|
; |
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
1 x2 |
|
1 x2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
|
1 |
|
|
|||||
arctgx |
|
|
; |
|
arcctgx |
|
|
. |
|
|
|||||
1 x2 |
|
1 x2 |
|
|
|||||||||||
Перваое из этих равенств доказано в п. 5.3. Остальные равенства доказываются аналогично с помощью теоремы и производной обратной функции (теорема 5.3). Доказать это самостоятельно.
5.5. Таблица производных и правил дифференцирования
Запишем правила дифференцирования и формулы производных основных элементарных функций.
Правила дифференцирования
1.f x g x f x g x ;
2.kf x kf x ; k const ;
3.f x g x f x g x f x g x ;
85
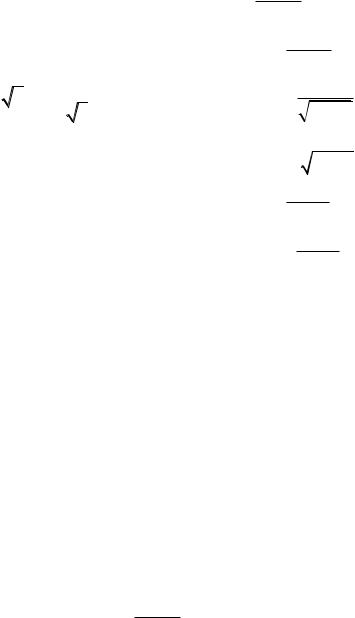
4. |
|
|
|
|
|
|
|
|
x g x f x g |
x |
; |
||||
f x f |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g x |
|
|
|
|
|
|
|
g2 x |
|
|
|||
5. |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
f x ; |
|
|
|
|
|
|||||||
f |
|
y |
|
|
|
|
|
||||||||
6. |
|
f g x |
|
|
f z |
|
|
g x . |
|
||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
z g(x) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Формулы дифференцирования
1.c 0 c const ;
2.x 1;
3. xn nxn 1; |
|
|
|
|
|
|
|
1 |
|
|
; |
|
|
|
x |
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
|
|
2 |
|
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
4. ax ax lna; |
|
ex ex; |
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
5. logax |
|
; |
|
lnx |
|
x |
; |
|
|
|||
xlna |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
6.sinx cosx;
7.cosx sinx;
9.tgx cos12 x;
10.сtgx sin12 x;
11.arcsinx  11 x2 ;
11 x2 ;
12. arccosx |
|
1 |
|
; |
|
|
|
|
|||
1 x2 |
|||||
|
|
|
|||
13.arctgx 1 1x2 ;
14.arcctgx 1 1x2 .
5.6. Механический смысл производной
Обозначим через S путь, пройденный движущимся телом за время от некоторого начального момента t0 до момента t. Каждому значению t соответст-
вует определенное значение S, так что S есть функция от t:
S S t .
Эта зависимость называется законом движения тела. Определим среднюю скорость Vср движения данного тела за промежуток времени t:
Vср Stt .
Если промежуток t достаточно мал, то значение средней скорости
86

близко к истинной в момент t. Уменьшая t, мы будем все ближе подходить к истинному значению скорости в момент t. На языке теории пределов определение мгновенной скорости V t можно сформулировать так:
V t lim |
S t |
lim |
S t t S t |
S t . |
|
t |
t |
||||
t 0 |
t 0 |
|
Пример. Для свободного падения тела в пустоте зависимость S t имеет
вид
S t gt22 ,
где g ‒ ускорение свободного падения.
Найдем мгновенную скорость движения тела в момент t:
V t S (t) gt22 gt.
Пример. В случае простых гармонических колебаний зависимость S t
выражается формулой
S t asin t,
где a ‒ постоянная амплитуда колебаний, ‒ постоянная частота. Для скорости гармонических колебаний получим
V t S t asin t a cos t.
Рассмотрим тонкий стержень длиной l одинакового по всей длине диаметра. Вещество в стержне расположено неоднородно, то есть в одном месте более плотно, в другом менее плотно. Примем за начало отсчета левый конец стержня (рис. 5.2).
0 |
l |
х |
Рис . 5.2. Тонкий стержень длиной l
Масса вещества является функцией координаты х, так что m m x . Средняя плотность вещества на участке x равна
87

m x m x x m x .
x x
Плотность вещества в сечении x определяется так:
x lim m x m x .
x 0 x
5.7. Геометрический смысл производной
Пусть x0 ‒ абсцисса точки M , принадлежащей кривой y f x (см. рис. 5.3). Выберем точку M1 на кривой с абсциссой x0 x. Через точки M и M1 проведем секущую рассматриваемой кривой. Из рис. 5.3 видно, что
k1 tg f xx0 .
Пусть x 0, то есть точка xстремится к точке x0. Если при этом секущая стремится к предельному положению T1MT , то прямую T1MT называют
касательной к кривой y f x в точке M .
Определение 5.3. Касательной к данной кривой в точке называется предельное положение секущей MM1, когда точка M1 стремится к точке M , оста-
ваясь на этой кривой.
Так как касательная есть прямая линия, то ее уравнение имеет вид y kx b,
где k ‒ угловой коэффициент касательной. |
|
|
|
|
|
|
||||||||
Так как k tg , |
то из определения 5.3 |
касательной и непрерывности |
||||||||||||
функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
tgx |
|
k |
; k 0; |
1; |
|
|
|
|
|
||||
x |
2 |
2;... |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
k tg M1N ) |
|||
имеем для углового коэффициента |
|
k |
1 |
секущей |
MM |
1 |
(где |
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
MN |
||
|
|
|
|
|
|
|
|
f f |
|
|
|
|
|
|
|
k |
limk |
|
lim |
x |
. |
|
|
|
|||||
|
|
x 0 1 |
|
|
x 0 |
x |
0 |
|
|
|
|
|
||
Таким образом, угловой коэффициент касательной совпадает со значени- |
||||||||||||||
ем производной f x |
в точкеx x0 . |
|
|
|
|
|
|
|
|
|
||||
88

y
y f x
f x0 x |
|
M1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
y |
T |
|
|
|
|
|
|
||
f x0 |
М |
|
|
|
|
|
|
N |
|
|
|||
|
|
|
|
|
||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О |
x0 |
x0 |
x |
х |
||
Т1 |
|
|
|
|
|
|
Рис. 5.3. Геометрический смысл производной |
|
|||||
Выведем уравнение касательной к кривой y f x в точкеM x0; f x0 . |
||||||
Так как касательная проходит через точку M x0; f x0 , то е |
координа- |
|||||
ты должны удовлетворять уравнению прямой |
y kx b, то есть |
|
||||
Так как k tg f x0 , то |
f x0 kx0 b. |
|
|
|
|
|
|
|
|
|
|
|
|
откуда |
f x0 f x0 x0 b, |
|
|
|
|
|
b f x0 f x0 x0 . |
|
|
|
|
||
|
|
|
|
|
||
Подставляя значение b в уравнение прямой |
|
y f (x0)x b, получим |
||||
уравнение касательной к кривой y f x в точке M x0; f x0 : |
|
|||||
f x f x0 f x0 x x0 . |
(5.1) |
|||||
89
