
Методическое пособие 659
.pdfУравнения (4.9) и (4.12) получены для того случая, когда все сочленения выполнены на основе вращательных кинематических пар. Аналогично можно вывести уравнения динамики механизма, имеющего кинематические пары поступательного типа. Пусть, например, сочленение с номером s реализует поступательное перемещение по координате qs. Нагрузочный момент в этом сочленении будет равен
Мнs = Fqshs, |
(4.13) |
где Fqs – сила, развиваемая в сочленении; |
|
||
hs – длина плеча в механизме преобразования вращатель- |
|||
ного движения в поступательное. |
|
|
|
Так как, согласно (1.85), справедливы равенства |
|||
qдs= nsqs/hs, qдs= ns qs/hs, |
q |
дs= ns qs/hs, (4.14) |
|
|
|
|
|
то в соответствии с (4.4) и (4.5) уравнения движения для поступательной степени подвижности будут иметь вид
|
|
s ns qs/hs = Мдs – Мсs( qs) – Мнs/ns, Мдs = kmsIs, |
|
||||||
J |
|
||||||||
|
|
|
|
|
|
|
(4.15) |
||
|
|
|
+ kmsIs = Uskms/Rs – kmskesns qs/Rshs, |
||||||
|
|
Lskms Is /Rs |
|
||||||
|
|
|
|
|
|
|
|
|
|
или в другой форме |
|
|
|
|
|||||
|
|
|
|
s ns |
qs = nshs[Мдs – Мсs( qs)] – Fqshs |
2 |
, |
|
|
|
|
J |
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
(4.16) |
|
||
Тэs Mдs + Мдs = Uskms/Rs – kmskesns qs/Rshs. |
|
|
Выражения системы (4.16) при поступательном перемещении отличаются от соответствующих уравнений системы (4.5) для вращательного движения при s=j лишь наличием параметра hs.
Векторная форма записи системы (4.16) имеет вид, аналогичный выражениям (4.6):
Os q |
= Ns [Мд – Мс( q )] – FqHs, |
|
|
|
|
|
(4.17) |
|
Тs М д + Мд = esU |
– cs q , |
|
|
|
|
|
|
|
|
|
80
где приняты следующие обозначения:
|
|
s |
ns |
2 |
}, |
q |
= {q1, |
q2, ..., |
qn} , |
Ns |
= diag{nshs}, |
|||
Os = diag{ J |
||||||||||||||
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
т |
М д = { |
M |
д1 , |
Mд2 |
, ..., |
|
т |
Мд = {Мд1, Мд2, ..., Мдn} , |
Mдn } , |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
Hs |
|
2 |
}, (4.18) |
||
Мс(q) ={Мс1(q1), |
Мс2(q2), ..., Мсn(qn)} , |
= diag{hs |
||||||||||||
Fq={ Fq1, Fq2, ..., Fqn}т, |
Тs = diag{Тэs}, |
|
|
|
||||||||||
es = diag{kms/Rs}, |
U = {U1, U2, ..., Un}т, |
|
||||||||||||
cs = diag{kmskesns/Rs}, |
q = {q1,q |
2, ..., |
qn} , |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
Матрицы Os, Ns, Hs, Тs, es и cs являются диагональными. |
||||||||||||||
Уравнения |
управляемого движения манипуляторов с |
|||||||||||||
учетом динамики приводов как поступательных, так и вращательных степеней подвижности имеют вид (4.9). Управляющими сигналами для данной модели являются управляющие напряжения U = {U1, U2, ..., Un}т.
Задачу синтеза алгоритмов управления по ускорению сформулируем следующим образом.
Пусть требуемое пространственное положение механизма характеризуется значениями кинематических переменных
qзад j = const, j = 1, 2 , ..., n .
В начальный момент времени t=0 состояние манипулятора характеризуется некоторыми значениями координат и
скоростей их изменения |
|
|
|
qj(0) = qj0, |
qj(0) = |
qj0, j = 1, 2, ..., n. |
(4.19) |
|
|
|
|
Требуется синтезировать такие алгоритмы вычисления управляющих напряжений, при которых исполнительный механизм переходит из начального состояния (4.19) в окрест-
ность точки qзад = (qзад1, qзад2, ..., qзадn)т и продолжает оставаться в этой окрестности бесконечно долго. Это требование
будем записывать символически в виде q(t) qзад.
В качестве дополнительного поставим условие, чтобы
процесс изменения кинематических переменных q(t) qзад при управлении движением соответствовал решению дифференциальных уравнений:
81
qjэ(t) + |
j1 qjэ(t) + |
j0qjэ(t) = |
j0qзадj, j = 1, 2, ..., n, (4.20) |
|
|
|
|
где qjэ(t), qjэ(t), qjэ(t) – эталонные процессы изменения во
времени ускорений, скоростей и перемещений по j-й координате;
j1, j0 – положительные коэффициенты.
Уравнение (4.20) можно записать в стандартной форме
qjэ(t) + 2 j qjэ(t)/Tj + qjэ(t)/Tj |
2 |
= qзадj/Tj |
. (4.21) |
|
|
|
2 |
|
|
Выражение (4.21) описывает известное из теории автоматического управления и широко применяемое в различных системах управления звено второго порядка, характеристики
которого определяются коэффициентом затухания j и постоянной времени Tj [8]–[11]. Сравнивая (4.20) и (4.21), получаем
следующие уравнения для определения коэффициентов j1 и
j0:
j1 = 2 j/Tj, |
j0 = 1/Tj2. |
(4.22) |
В таблице приведены числовые показатели, характеризующие динамические свойства системы, описываемой урав-
нением (4.21). В случае j = 1 уравнение (4.21) соответствует апериодическому звену второго порядка, время переходного
процесса tj 5Tj. При уменьшении коэффициента j увеличивается колебательность процесса, что приводит к появлению и
нарастанию перерегулирования j.
Зависимость параметров tj и j от коэффициента затухания j
j |
j, % |
tj |
j |
j, % |
tj |
1,00 |
0,0 |
5Tj |
0,50 |
18 |
6Tj |
0,71 |
4,3 |
3Tj |
0,25 |
42 |
12Tj |
Таким образом, по заданным требованиям к динамике управляемой системы, характеризующимся временем tj пере-
ходного процесса и перерегулированием j, можно вычислить
82

с помощью данных таблицы коэффициенты уравнения (4.20) в соответствии с (4.22). Длительность tj определяется практически по условиям физической реализуемости назначаемых динамических характеристик проектируемой системы такой,
чтобы tj > 3Tmj.
Электромеханическая постоянная времени Tmj равна
|
|
j Rj/kmjkej. |
|
Tmj = J |
(4.23) |
||
В уравнении (4.23) через Jj обозначены приведенные к
валу двигателя с параметрами Rj, kmj и kej вращающиеся и (или) движущиеся поступательно инерционные массы j-й координаты манипулятора в сумме с моментом инерции якоря двигателя.
Реальные законы изменения перемещений qj(t), скоростей qj(t) и ускорений qj(t) всегда отличаются от заданных.
Принцип управления по ускорению предполагает сравнение эталонного процесса изменения ускорения qjэ(t) с реальным
qj(t) и выработку управляющих воздействий, направленных на минимизацию рассогласования qjэ(t) – qj(t). При этом заданные управляющие моменты двигателей формируются в
соответствии с выражением |
|
kjj = const, |
|
М дjэ(t) = kjj( jэ – qj), |
(4.24) |
||
|
|
|
|
|
|
|
|
где jэ = qjэ.
Независимо от причин, вызывающих отклонение реальных ускорений qj от эталонных jэ, заданный момент Мдjэ
изменяется таким образом, чтобы скомпенсировать появившееся отклонение. Благодаря этому алгоритмы управления по ускорению придают системам свойства естественной адаптивности и слабой чувствительности по отношению к изменению параметров управляемых объектов, а также к координатным возмущениям.
Рассмотрим формирование структуры алгоритмов управления по ускорению.
83
На основании (4.20) получим выражение для определения эталонного процесса изменения ускорения по j-й координате
jэ(qj, |
qj) = j0 |
(qзадj – qj) – j1 qj. |
(4.25) |
|
|
|
|
Из второго уравнения системы (4.9) для j-й координаты получим
Тjэ М дjэ+Мдjэ = ejjUj – cjj qj . |
(4.26) |
|
|
|
На основании (4.24) и (4.26) получим следующее выражение:
Тjэkjj( jэ – qj) + Мдjэ = ejjUj – cjj qj. |
(4.27) |
|
|
|
|
Из выражений (4.24), (4.25) и (4.27) получим систему уравнений синтезированного алгоритма управления по ускорению:
–1 |
|
|
|
|
Мдjэ], |
|
Uj = ejj [Тjэkjj( jэ – qj) + cjj q + |
(4.28) |
|||||
jэ(qj, |
qj) = j0 |
(qзадj – qj) – j1 qj, |
||||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
Мдjэ(t) = kjj ( jэ – qj)dt. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Векторная форма уравнений (4.28) имеет следующий |
||||||
вид: |
–1 |
|
|
|
|
|
U = e |
|
|
|
|
|
|
|
[Тэk(Еэ– q ) + c q + Мдэ], |
(4.29) |
||||
Еэ(q,q) = Г0(qзад – q) – Г1 q , |
|
|||||
|
|
|
|
|
|
|
Мдэ(t) = k t (Еэ – q )dt.
0
В уравнениях системы (4.29) приняты следующие обозначения:
U = {U1, U2, ..., Un}т, |
e–1 = diag{ejj–1}, |
Тэ = diag{Тэj}, |
|||||
K = diag{kjj}, Еэ = { 1э, 2э, ..., nэ} , |
q = {q |
1, q |
2, ..., qn} , |
||||
|
|
т |
|
|
|
|
т |
c = diag{cjj}, |
q |
= {q1, |
q2, ..., |
qn} , |
(4.30) |
||
|
|
|
|
|
|
т |
|
84
Мдэ = {Мд1э, Мд2э, ..., Мдnэ}т, |
q = {q1, q2, ..., qn}т, |
|
Г0 = diag{ j0}, |
Г1 = diag{ j1}. |
|
Структурная схема, соответствующая системе уравнений (4.29), приведена на рис. 4.3. По информации о состоянии управляемого объекта q(t), q (t) во внешнем контуре вычисля-
ется требуемое ускорение Еэ. Величина Еэ поступает на вход внутреннего контура отработки ускорения. Его выходной переменной является фактическое ускорение q . В структуру
внутреннего контура входят двигатели электроприводов и исполнительный механизм ИМ.
В том случае, когда можно не учитывать инерционность электрических процессов в якорных цепях двигателей (Тjэ= 0), управляющие напряжения можно определять из соотношения
U j (t) = jj({ jэ – |
qj), |
|
jj = const. |
(4.31) |
|
|
|
|
|
|
|
|
|
|
Векторная форма записи уравнений алгоритма приобре- |
||||
тает вид |
|
|
q ), |
|
U (t) = (Еэ – |
|
|||
|
|
|
|
(4.32) |
|
|
|
||
|
|
– |
|
|
Еэ(q,q) = Г0(qзад |
q) – Г1q , |
|
||
где = diag{ jj}.
Структурная схема замкнутой системы, построенной в соответствии с (4.32), приведена на рис. 4.4.
Внешний контур формирует сигнал задания ускорения Еэ, который поступает на вход контура отработки ускорения. Пропорционально отклонению Еэ– q вычисляется скорость
U изменения управляющего напряжения, которая после интегрирования поступает в управляющие цепи исполнительных двигателей.
85
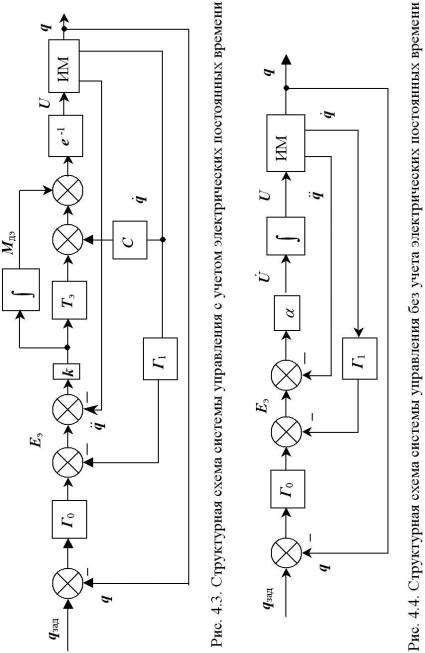
86
Структура этой системы аналогична структуре, изображенной на рис. 4.3. Различие состоит в том, что в данном случае не вычисляются требуемые значения электромагнитных моментов двигателей Мдэ.
Для вычисления управляющих напряжений в системе, изображенной на рис. 4.4, необходимо иметь информацию о вторых производных q (t). В исполнительных механизмах не
всегда оказывается возможным измерять ускорения кинематических переменных. Практически q (t) могут быть получены
с помощью дифференцирующих устройств, реализованных на элементах аналоговой вычислительной техники, либо с помощью алгоритмов численного дифференцирования, если для управления используются цифровые вычислительные машины.
Однако алгоритмы управления целесообразно реализовать без измерения ускорений управляемых координат. Для этого необходимо уравнения алгоритма представить в интегральной форме.
Выполняя интегрирование по времени обеих частей уравнения (4.31), получим
t |
qj(t) ]. |
(4.33) |
Uj(t) = jj[ jэ (q,q ) dt – |
||
|
|
|
0 |
|
|
Здесь начальные значения Uj(0), U j(0) приняты равными нулю. В векторной форме уравнения алгоритма по ускорению приобретают вид
t |
|
U(t) = [ Еэ (q,q ) dt – q (t) ], |
|
|
|
0 |
(4.34) |
Еэ(q,q ) = Г0(qзад – q) – Г1 q .
Структурная схема системы управления, использующей алгоритм (4.34), приведена на рис. 4.5. В данном случае при вычислении напряжений U(t) не используются ускорения q (t).
Это позволяет легко реализовать алгоритмы управления по ускорению на практике.
87

qзад |
|
ЕЭ |
U |
q |
|
Г0 |
|
||||
|
|
ИМ |
|||
|
q |
q |
q |
|
|
|
|
|
|||
|
|
q |
|||
|
|
|
|||
|
|
Г1 |
|
|
Рис. 4.5. Структурная схема системы управления без использования датчиков ускорения
4.3. Свойства и параметры систем, управляемых по ускорению
Рассмотрим систему, структурная схема которой приведена на рис. 4.5. Исполнительный механизм ИМ описывается выражением (4.12). Выразим из (4.12) ускорение q :
q |
={ N[eU – c q–Мс |
( q )] – B(q,q ) – C(q) } / А(q). |
(4.35) |
||
|
|
|
|
~ |
|
Из (4.35) следует, что ускорение q |
является функцией |
||||
|
|
|
|
|
и век- |
вектора обобщенных координат q, его производной q |
|||||
|
|
|
|
|
|
тора управляющих напряжений U, т. е. |
|
|
|||
|
q |
= E(q, q , U). |
|
(4.36) |
|
|
|
|
|
|
|
После дифференцирования (4.36) по времени получим
q = a1q + a2 q + dU ,
где a1, a2, d – матрицы размера n n.
Выражения для определения матриц a1, a2 и d: a1 = [ j/ qi] = [a1ji], a2 = [ j/ qi] = [a2ji], d = [ j/ Ui] = [dji],
где j = 1, 2, ..., n – номера строк матриц;
i = 1, 2, ..., n – номера столбцов матриц.
(4.37)
(4.38)
88
На основе уравнений (4.32) и (4.37) получим следующее выражение:
q + (d – a2)q + (d Г1 – a1)q + d Г0 q = d Г0 qзад. (4.39)
Это векторное уравнение третьего порядка описывает динамику замкнутой системы с алгоритмом управления (4.32). Поскольку размерность вектора q равна n, общий порядок скалярных уравнений, соответствующих (4.39), равен 3n.
Рассмотрим преобразования уравнения (4.39) при бесконечно высоком быстродействии контуров ускорения. Для этого умножим каждый член уравнения (4.39) на квадратную диагональную матрицу 0–1 = diag{1/ jj}, а затем выполним
предельный переход при jj .
Указанная операция означает, что каждое уравнение
q j+(d –a2)j q +(d Г1–a1)j q +(d Г0)jq=(d Г0)jqзад (4.40)
умножается на 1/ jj, а затем вычисляются соответствующие пределы при jj . Отметим, что символом (...)j обозначена j-я строка матрицы, стоящей в скобке.
Справедливо следующее предельное равенство:
lim |
( 0–1 ) = 1. |
(4.41) |
j j |
|
|
В результате преобразований можно получить выражения:
lim |
( 0–1d ) = d, |
lim |
( 0–1 d Г1) = dГ1, |
||
j j |
|
|
j j |
|
|
lim |
( 0–1 |
d Г0) |
= dГ0, |
lim |
( 0–1as) = 0. |
j j |
|
|
j j |
|
|
Умножая (4.39) на 0–1, получим уравнение
0–1 q + 0–1d q – 0–1a2 q + 0–1d Г1 q –
–0–1a1 q+ 0–1d Г0q = 0–1d Г0qзад.
(4.42)
(4.43)
После выполнения предельных переходов (4.42) уравнение (4.43) преобразуется
d q |
+dГ1 q +dГ0q = dГ0qзад. |
(4.44) |
|
|
|
89
