
Методическое пособие 659
.pdf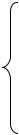
до + /2. Так как изменяется в общем случае в пределах от
– до + , то для его определения необходимо пользоваться соотношениями
|
arctg (x1 / x2) |
при |
x2>0, |
|
|
|
+ /2 |
|
при |
x2=0, x1>0, |
|
= |
/2 |
|
при |
x2=0, x1<0, |
(2.15) |
|
arctg (x1 |
/ x2) + |
при |
x2<0, x1>0, |
|
|
arctg (x1 |
/ x2) – |
при |
x2<0, x1<0. |
|
2.4. Прямая и обратная задачи кинематики при управлении манипулятором в сферической системе координат
Связь между декартовыми координатами x1, x2, x3 гру-
за массой m и обобщенными координатами 1, 2, r для расчетной схемы, представленной на рис. 1.3, имеет вид
x1 r sin 1 cos 2 ,
x2 l r sin 2 , |
(2.16) |
x3 r cos 1 cos 2 .
Уравнения кинематики для скоростей получаются в результате дифференцирования (2.16) по времени:
x1 |
r sin 1 cos 2 |
r 1 cos 1 cos 2 |
r |
2 sin 1 sin 2, |
|
|
|
|
|
|
|
|
x2 r sin |
2 r 2 cos 2, |
(2.17) |
||
x3 |
|
|
|
|
2 cos 1 sin . |
r cos 1 cos 2 |
r |
1 sin 1 cos 2 |
r |
||
|
|
|
|
|
|
Обозначим q1= 1, q2= 2, q3=r. Тогда уравнения (2.16) можно представить в следующем виде:
|
q |
|
sinq cosq |
|
|
|
X = F(q) = |
|
3 |
1 |
2 |
|
(2.18) |
l |
q3sinq2 |
|
. |
|||
|
|
|
|
|
|
|
|
q3cosq1cosq2 |
|
|
|||
40
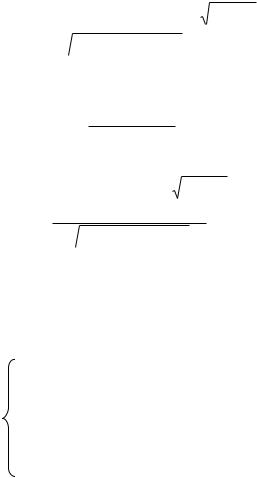
В этом случае матрица Якоби |
|
|
|
|
|
|
|
|||||||
|
q3cosq1cosq |
2 |
|
q3sinq1sinq2 |
sinq1cosq2 |
|
|
|
||||||
J(q) = |
|
0 |
|
|
|
|
q3cosq2 |
sinq2 |
|
|
(2.19) |
|||
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
q3cosq1sinq2 |
|
|
|
|
|
|
|
|
q3sinq1cosq2 |
|
cosq1cosq2 |
|
||||||||||
Обратная задача для рассматриваемого манипулятора |
||||||||||||||
имеет следующее решение: |
|
|
|
|
|
|
|
|||||||
|
|
x |
|
|
|
|
|
x |
2 |
l |
|
|
|
|
|
|
1 arctg |
|
1 |
|
, |
2 arctg |
|
|
|
, |
|
||
|
|
|
|
|
|
|
|
|||||||
|
|
x |
|
|
|
|
|
x |
2 |
2 |
|
|
(2.20) |
|
|
|
|
3 |
|
|
|
1 |
x3 |
|
|
||||
r  (x2 l)2 x12 x32 .
(x2 l)2 x12 x32 .
Скорости изменения обобщенных координат находим дифференцированием по времени уравнений (2.20):
1 x1 x3 x1 x3 ,
x12 x32
|
|
|
2 |
2 |
|
|
|
|
|
2 |
x2 |
(x1 |
x3) |
(x2 l)(x1 x1 x3 x3) |
, |
(2.21) |
|
|
|
|
(x12 (x2 l)2 x32) |
x12 x32 |
|
|
||
|
|
|
|
|
||||
r x1 x1 (x2 l)x2 x3 x3 .
 x12 (x2 l)2 x32
x12 (x2 l)2 x32
В первом уравнении системы (2.21) необходимо принимать значения arctg(x1/x3), которые ограничены пределами от
– /2 до + /2. Так как 1 изменяется в общем случае в пре-
делах от – до + , то для его определения необходимо пользоваться соотношениями:
|
arctg (x1 / x3) |
при |
x3>0, |
|
|
+ /2 |
|
при |
x3=0, x1>0, |
1= |
/2 |
|
при |
x3=0, x1<0, (2.22) |
|
arctg (x1 |
/ x3) + |
при |
x3<0, x1>0, |
|
arctg (x1 |
/ x3) – |
при |
x3<0, x1<0. |
41
Угол 2 изменяется в пределах от – /2 до + /2, его
значения вычисляются по (2.20) с учетом того, что 2 = /2
при x1 = x3 = 0.
2.5. Прямая и обратная задачи кинематики при управлении манипулятором в угловой системе координат
Согласно расчетной схеме рассматриваемого манипулятора, приведенной на рис. 1.4, прямая задача кинематики решается в следующем виде:
|
x1 [l2 cos 2 l3 cos( 2 3)] sin 1, |
|
|
|||
|
|
x2 l2 sin 2 l3 sin( 2 3 ) l1 , |
|
(2.23) |
||
|
x3 [l2 cos 2 l3 cos( 2 3)] cos 1 . |
|
|
|||
Дифференцируя (2.23) по времени, получим уравнения |
||||||
кинематики для скоростей |
|
|
|
|
||
x1 [ l2 |
2 |
sin 2 l3( 2 3) sin( 2 3)] sin |
1 |
|
||
|
|
|
|
|
|
|
[l2 cos 2 l3 cos( 2 3)] cos 1 1, |
|
|
||||
x2 l |
2 |
2 cos 2 l3( 2 |
|
|
|
(2.24) |
3) cos( 2 3), |
|
|||||
|
|
|
|
sin( 2 3)] cos 1 |
||
x3 [ l2 2 |
sin 2 l3( 2 3) |
|||||
|
|
|
|
|
|
|
[l2 cos 2 l3 cos( 2 3)] sin 1 1. |
|
|
||||
|
|
|
|
|
|
|
Обозначим q1= 1, q2= 2, q3= 3, тогда уравнения |
||||||
(2.23) записываются в виде |
|
|
|
|
||
|
|
|
l3 cos(q2 q3)]sinq1 |
|
|
|
|
|
[l2 cosq2 |
|
|
||
|
|
|
|
|
. (2.25) |
|
X = F(q) = l2 sinq2 l3 sin(q2 q3) l1 |
|
|||||
|
|
|
|
|
|
|
|
|
[l2 cosq2 |
l3 cos(q2 q3)]cosq1 |
|
||
Дифференцируя (2.25), можно получить выражение для матрицы J(q), входящей в векторное уравнение кинематики для скоростей (2.2). Это выражение слишком громоздкое и поэтому не приводится.
42
Из первого и третьего уравнений системы (2.23) получим
|
|
|
|
|
x1 |
|
(2.26) |
|
|||
1 arctg |
. |
||
x3 |
|
|
|
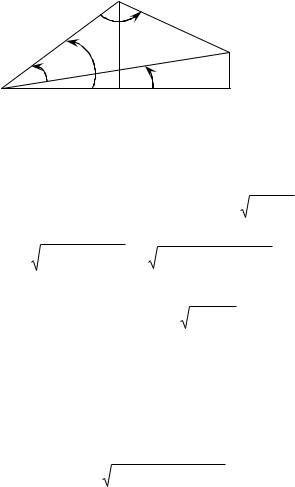
Обобщенные координаты 2 и 3 можно выразить из треугольников, представленных на рис. 2.1 и соответствующих верхней части рис. 1.4.
|
B |
|
|
2 |
3 |
|
|
|
С |
||
2 |
2 |
D |
|
A |
|||
|
Рис. 2.1. Схема для определения обобщенных координат 2 и 3
Величины отрезков, изображенных на рис. 2.1, равны
AB =l2, BC =l3, CD =x2 – l1, |
AD = |
|
x2 |
x2 |
. (2.27) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
Из треугольника ACD находим |
|
|
|
|
|
|
|
|
|
||||||||||||||
AC = |
|
AD |
|
2 |
|
|
CD |
|
2 |
= x |
2 x2 (x |
l )2 |
, |
(2.28) |
|||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
CD |
|
|
|
|
|
x2 l1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
'= arctg |
|
|
|
|
= arctg |
|
|
. |
|
|
(2.29) |
|||||||||||
|
|
|
|
|
|||||||||||||||||||
|
AD |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
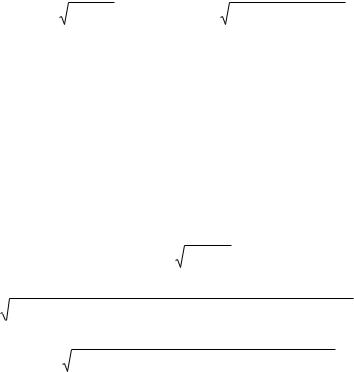
Из треугольника ABC в соответствии с теоремой косинусов определяем углы 2'' и 3:
|
|
|
AB |
|
2 |
|
AC |
|
2 |
|
BC |
|
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2''=arccos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
AB |
|
AC |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
l2 l |
2 x |
2 |
l |
1 |
2 x |
|
2 x |
2 |
|
|
|
|
||||||||||||||||
=arccos |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
, |
(2.30) |
||||
2l |
|
|
|
l )2 x2 x2 |
|
|
||||||||||||||||||||||
|
|
(x |
|
|
|
|
|
|||||||||||||||||||||
|
2 |
2 |
|
1 |
|
1 |
3 |
|
|
|
|
|
||||||||||||||||
43
|
|
|
|
|
AB |
|
2 |
|
BC |
|
2 |
|
|
AC |
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
3 |
= arccos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
AB |
|
BC |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
2 |
[(x2 l1) |
2 |
2 |
|
|
|
2 |
] |
|
|||||||||||||||
arccos |
l2 |
l3 |
|
x1 |
x3 |
. |
(2.31) |
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2l2l3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Таким образом, для обобщенных координат 2 и 3 из выражений (2.29)–(2.31) имеем
|
|
x |
2 |
l |
1 |
|
|
|
l2 l |
2 (x |
2 |
l ) |
2 x |
2 |
x |
2 |
|
|||||||||
2 |
arctg |
|
|
|
|
|
arccos |
2 |
3 |
|
|
|
1 |
|
|
|
1 |
|
3 |
|
, (2.32) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
|
2 |
|
|
|
|
2l2 |
|
(x2 |
l1) |
2 |
|
2 |
|
2 |
|
|
|
|||||
|
|
x1 |
x3 |
|
|
|
|
|
|
x1 |
x3 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
2 |
[(x2 l |
1) |
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
3 |
arccos |
l2 |
l3 |
|
x1 |
x3] |
. |
|
|
|
|
(2.33) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2l2l3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Уравнения (2.26), (2.32) и (2.33) позволяют решить обратную задачу кинематики для перемещений. Дифференцируя их по времени, получим уравнения для определения скоростей изменения обобщенных координат
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х1 x3 x1 х 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
(2.34) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
x12 x32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 (x |
|
|
(x2 l |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
|
2 |
х |
1 |
x3) |
1)(x1 х1 x |
3 х 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
[x |
2 |
x2 |
(x |
|
l )2] x2 x2 |
|
|
x12 |
x32 (x2 l1)2 |
|
||||||||||||||||||||
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
1 |
3 |
|
|
|
|
1 |
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|
2 |
|
|
|
l1) |
2 |
] |
|
|
|
||||
|
(x1 х1 x3 |
х3 (x2 l1) |
х2)[l3 l2 |
x1 |
x3 (x2 |
|
, |
(2.35) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
4l2 |
[x2 x2 (x |
2 |
l )2 |
] [l2 |
l2 |
x2 x2 |
(x |
2 |
l )2 |
]2 |
|
|
|
|||||||||||||||||||
|
|
2 |
1 |
|
|
3 |
|
|
|
|
1 |
|
|
2 |
3 |
|
1 |
|
|
3 |
|
3] |
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2[(x2 l1) х |
2 x1 |
х1 x3 х |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
(2.36) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2l |
2 |
l |
3 |
)2 |
[l |
2 |
l2 |
[(x |
2 |
l )2 |
x2 |
x2 |
]]2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
1 |
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|||||
Решение прямых и обратных задач о положении и скорости используется при формировании кинематических алгоритмов управления манипулятором.
44
2.6. Кинематические алгоритмы управления
Кинематические алгоритмы строятся по кинематическим уравнениям. Различают кинематические алгоритмы нулевого и первого порядка, если в качестве управляющих параметров используются соответственно кинематические переменные и их скорости изменения (первые производные по времени).
Рассмотрим особенности этих алгоритмов. Кинематический алгоритм нулевого порядка основан на
реализации соотношения
qзад = F –1(Xзад), |
(2.37) |
где qзад – вектор заданных значений обобщенных координат манипулятора;
Xзад – вектор заданных значений декартовых координат рабочего органа.
Уравнение (2.37) решает обратную задачу кинематики о положении, т. е. по координатам целевой точки в базовой системе отсчета определяет вектор обобщенных координат, который поступает на входы приводных систем робота в качестве задающих воздействий. Предполагается при этом, что алгоритмы приводной системы синтезированы, электроприводы замкнуты по положению, т. е. по координатам qs, s = 1, 2, 3, ..., n.
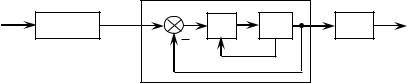
Особенность управления состоит в том, что оно осуществляется по разомкнутой схеме, текущее состояние исполнительного механизма не учитывается при формировании управляющих воздействий на приводы. Структурная схема, отвечающая рассмотренному алгоритму, приведена на рис. 2.2.
Хзад |
qзад |
|
|
q |
X |
F–1(Xзад) |
ПС |
ИМ |
F(q) |
||
|
q |
|
|
|
|
|
|
q |
|
|
|
Рис. 2.2. Структурная схема системы, управляемой по положению
45
На рис. 2.2 приняты обозначения: ПС – приводная система; ИМ – исполнительный механизм.
Практическое применение алгоритмов нулевого порядка ограничено теми ситуациями, когда допустимо программное управление без обратных связей.
Кинематический алгоритм первого порядка использует решение обратной задачи кинематики для скоростей
qзад(t) = J |
–1 |
|
(2.38) |
|
[q(t)] X зад(t), |
||
|
|
|
|
где qзад(t) – вектор заданных значений скоростей обобщенных координат манипулятора;
X зад(t)– вектор заданных значений скоростей декартовых координат рабочего органа.
Вектор X(t) текущих базовых координат вычисляется по уравнению (2.1) и вектору q(t) измеренных значений скоростей обобщенных координат. При сравнении векторов Xзад(t) и
X(t) получается вектор X зад(t) корректирующих внешних скоростей, используемый для того, чтобы уменьшить ошибку позиционирования. Вектор qзад(t) требуемых скоростей сочле-
нений вычисляется из (2.38). Приводные системы, замкнутые по положению, отрабатывают командные значения обобщенных координат qзад(t), вычисленные путем интегрирования заданных скоростей q зад(t). Возможна и другая схема управле-
ния, в которой приводы, управляемые по скорости, непосредственно отрабатывают сигналы q зад(t).
Рассмотренный способ управления называется управлением по вектору скорости. Данный способ реализуется во множестве вариантов, отличающихся алгоритмами формиро-
вания вектора Х зад(t) по результату сравнения заданного Xзад(t) и фактического X(t) перемещений рабочего органа, способами решения уравнения (2.38), а также связи с конкретными приводными системами. Информацию об управлении по вектору скорости можно получить из [3], [4].
46
Рассмотрим один из вариантов синтеза управления по вектору скорости для трехкоординатного манипулятора, приводные системы которого замкнуты по положению.
Задачу сформулируем следующим образом. В начальный момент t = 0 положение контролируемой точки исполнительного механизма характеризуется значениями
xs(0) = xs0 |
, xs (0) = xs0 , s = 1, 2, 3. |
(2.39) |
|
|
|
|
|
Требуется осуществить движение, при котором контролируемая точка исполнительного механизма перемещается в
окрестность неподвижной точки Xзад = (xзад1, xзад2, xзад3)т. При этом процесс xs(t) xзадs должен соответствовать решению
дифференциальных уравнений
xsэ (t) + K1s xsэ (t) + K0s xsэ(t) = K0s xзадs, s = 1, 2, 3. (2.40) |
|
|
|
Эталонный процесс xsэ(t) xзадs реализуется в том случае, когда ускорение
xsэ (t) = K0s(xзадs – xsэ(t)) – K1s xsэ (t), |
(2.41) |
|
|
|
|
поэтому будем определять требуемое ускорение из уравнения
xsэ (t) = asэ(xs, xs ) = K0s(xзадs – xs(t)) – K1s xs (t). (2.42)
После интегрирования выражения (2.42) получим уравнение для определения требуемой скорости
t |
|
Vsэ(t) = K0s (xзадs – xs(t))dt – K1s xs (t). |
(2.43) |
0 |
|
В векторной форме управление по вектору скорости описывается следующими уравнениями:
Vэ(t) = K0 t |
(Xзад |
– X(t))dt – K1X(t), |
|
|
0 |
|
–1 |
(q) Vэ(t), |
(2.44) |
|
|
|||
qэ (t) = J |
|
|||
qэ(t) = t qэ(t)dt,
0
47
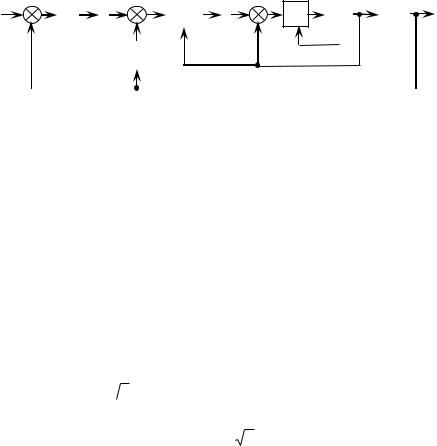
где K0 = diag{K0s}, K1 = diag{K1s} – диагональные матрицы. Структурная схема системы, управляемой по вектору
скорости, представлена на рис. 2.3.
В том случае, если приводные системы замкнуты по скорости, на них поступает вектор qэ без дополнительного
интегрирования.
Хзад |
|
|
|
|
|
Vэ |
qэ qэ |
|
|
|
|
q |
|
X |
||||||||
K0 |
|
|
|
|
|
|
J-1(q) |
|
|
|
|
ПС |
ИМ |
|
F(q) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
q |
|
q |
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
K1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.3. Структурная схема системы, управляемой по вектору скорости
Необходимо отметить, что равенство X(t) = Xэ(t) точно реализуется только в идеальном случае, когда требуемое зна-
чение qэ(t) (или qэ(t)) отрабатывается мгновенно, т. е. когда
система приводов и исполнительный механизм безынерцион-
ны. Чтобы эталонный процесс xsэ(t) xзадs был физически реализуем, числовые значения K0s, K1s необходимо назначать с
учетом динамики приводной системы и манипулятора.
Пусть динамика контуров управления по каждой степени подвижности аппроксимируется дифференциальными уравнениями
Тs |
qs + 2 s qs + qs = qзадs. |
(2.45) |
|
2 |
|
|
|
При s  2 /2 расчет параметров рекомендуется выполнять по формулам [5]
2 /2 расчет параметров рекомендуется выполнять по формулам [5]
K |
|
|
1 |
, K |
|
2 |
, s 1, 2, 3, |
(2.46) |
|
N2T2 |
N T |
||||||
|
0s |
|
1s |
|
|
|
||
|
|
|
s s |
|
|
s s |
|
|
где Ns = 5–6.
48
Контрольные вопросы
1.Какие задачи возникают при управлении манипуляторами, и какие уровни включаются в состав системы управления для решения этих задач?
2.Какие виды управления применяются в манипуляционных роботах?
3.Дайте определение прямой и обратной задач кинематики и обоснуйте необходимость их решения.
4.Запишите кинематические уравнения в скалярной и векторной формах и поясните физический смысл входящих в них переменных.
5.Решите прямую и обратную задачи кинематики для манипулятора, работающего в цилиндрической системе координат.
6.Выведите уравнения, позволяющие определить декартовы координаты рабочего органа по обобщенным координатам для манипулятора, работающего в сферической системе координат.
7.Решите обратную задачу кинематики для манипулятора, работающего в сферической системе координат.
8.Получите выражения для решения прямой задачи кинематики для манипулятора, работающего в угловой системе координат.
9.Выведите уравнения, позволяющие определить обобщенные координаты манипулятора, работающего в угловой системе координат, по декартовым координатам рабочего органа.
10.Каковы особенности кинематического алгоритма управления по положению?
11.В чем сущность способа управления по вектору ско-
рости?
12.Получите структурную схему системы, построенной
всоответствии с кинематическим алгоритмом управления по скорости.
49
